풀스택 웹🌐 개발자 지망생 🧑🏽💻
➕ 인공지능 관심 🤖
Categories
-
┣
▶ COMPUTER_SCIENCE
📂: 7 -
┣
▶ WEB
📂: 3 -
┣
▶ ETC
📂: 3-
┃
┣
ETCS
📄: 10 -
┃
┣
SUBBRAIN 개발기
📄: 5 -
┃
┗
YOS 개발기
📄: 1
-
┃
┣
-
┗
▶ AI
📂: 9-
┣
AITOOLS
📄: 3 -
┣
CV
📄: 2 -
┣
DEEP_LEARNING
📄: 1 -
┣
DATA_VIS
📄: 2 -
┣
GRAPH
📄: 1 -
┣
LIGHTWEIGHT
📄: 1 -
┣
MATH
📄: 1 -
┣
NLP
📄: 3 -
┗
STRUCTURED_DATA
📄: 2
-
┣
알고리즘 수학 기본-기하, 이항 분포
알고리즘을 위한 수학 - 기하, 이항 분포(geometric and binomial distributions)
_Introduction to Algorithm, 3rd, Cormen_을 토대로 정리한 내용입니다.
일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.
추가로 존이(mykepzzang)님의 블로그 에서 내용을 발췌하였다.
이 장에서는 분포의 표기법, 정의, 속성 같은 기본적인 것만 배운다. 들어가기에 앞서 확률에 대한 기본적인 이해가 필요하므로 알고리즘을 위한 수학 확률편 , 확률 변수편 을 보고 오는 것을 추천한다.
베르누이 시행의 분포 (Bernoulli trial Distribution)
베르누이 시행 (Bernoulli trial)은 동전 던지기처럼 상호 독립적인 2가지 결과(성공, 실패)만 나올 수 있는 경험을 의미하며, 보통은 두 결과 모두 동등하게 절반의 확률이다.
베르누이 시행에는 중요한 분포로 기하 분포와 이항 분포가 존재한다.
기하 분포 (The geometric distribution)
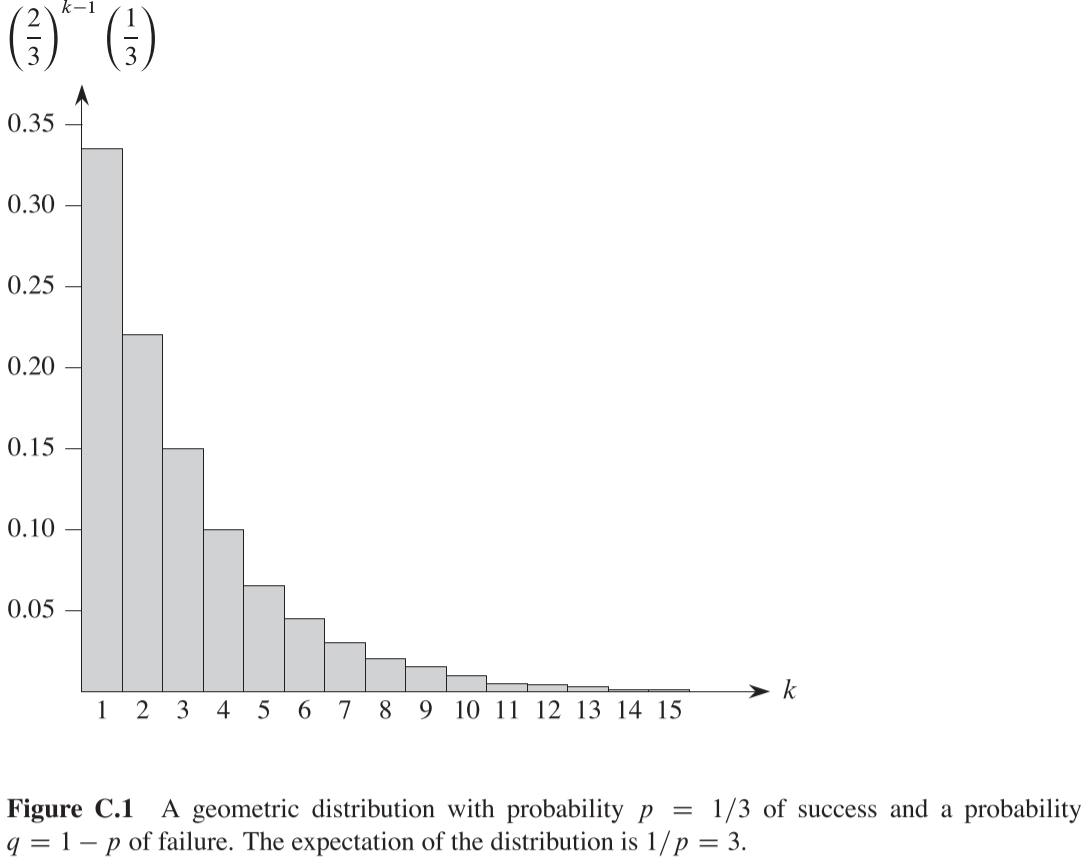
아래는 성공 확률과 실패 확률이 각각 $p,\ q=1-p$인 베르누이 시행의 시도에 대해, 확률 변수 X를 성공할 때까지 경험을 시도한 횟수라고 가정하면, $k \geq 1$일 때, 다음과 같은 확률을 구할 수 있다.
$\Pr{X=k}=q^{k-1}p$
이때 k-1의 실패 뒤에 k번재에 성공하게 되며, 이러한 식이 만족하는 확률 분포를 기하 분포라고 하며, Figure 1과 같은 모습이다.
또한, q < 1을 가정하고, 기하 분포의 기대값을 다음과 같이 구할 수 있다.
\[\begin{align} E[X]&=\sum_{k=1}^\infty kq^{k-1}p \\&=\frac{p}{q}\sum^\infty_{k=0}kq^k \\&=\frac{p}{q}\cdot\frac{q}{(1-q)^2} \\&=\frac{p}{q}\cdot\frac{q}{p^2} \\&=1/p \end{align}\]따라서, 성공을 얻는데 평균적으로 1/p 번의 시도가 필요하며, 다음과 같이 분산을 구할 수 있다.
$Var[X]=q/p^2$
예시로, 우리가 반복적으로 두개의 주사위를 던져 합이 7이나 11이 나오기 위해선, 36가지의 가능한 결과에서 6개의 합이 7인 경우와 2개의 합이 11인 경우가 존재한다. 따라서 성공 확률 $p=8/36=2/9$이며, 평균적으로 4.5회 던져야 성공할 수 있다.
이항 분포(The binomial distribution)
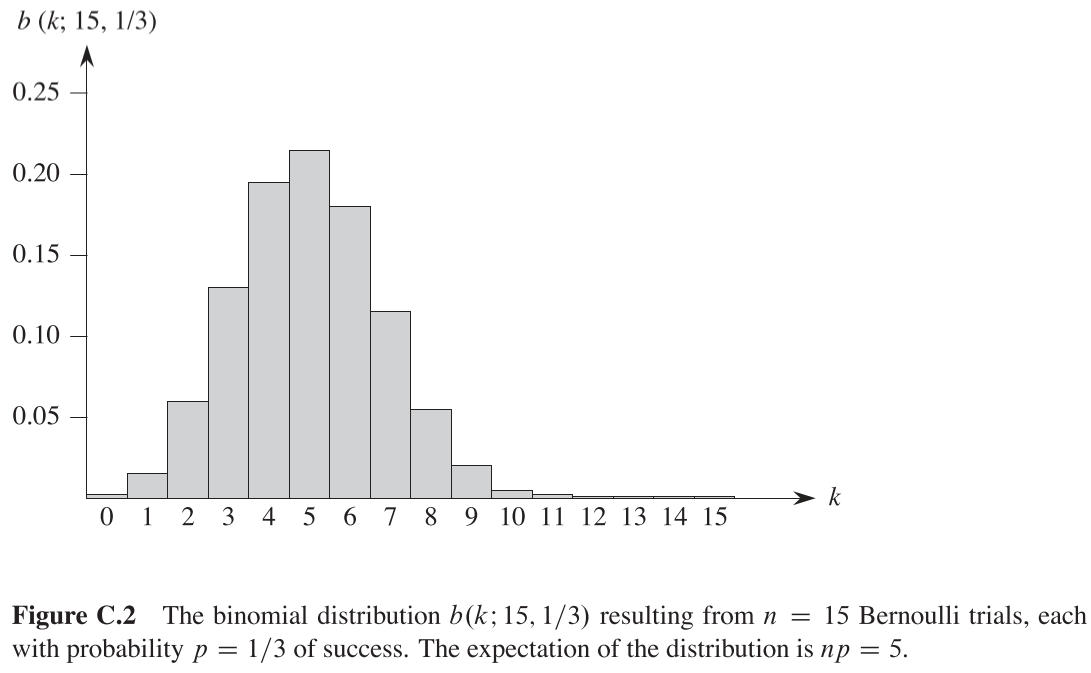
n번 시도에 대한 성공 횟수를 확률 변수 X로 놓는다면, $0 \leq k \leq n$일 때, 각기 일어날 확률이 $p^kq^{n-k}$이며, 총 $\binom{n}{k}$개의 방법이 존재하므로, 다음 같은 확률이 나온다.
\(\Pr\{X=k\}=\binom{n}{k}p^kq^{n-k}\)
위와 같은 식을 만족하는 확률 분포를 이항 분포(binomial distribution)라고 하며, Figure 2와 같이 표현된다.
“이항”은 위의 식이 전개시, $(p+q)^n$의 전개식 처럼 보이기 때문에 붙여진 이름이며, $p=1-q$일 때, 위 식을 아래와 같이 표기하기도 한다.
\(b(k;n,p)=\binom{n}{k} p^k(1-p)^{n-k}\)
또한, 확률 공리 “모든 사건들의 확률의 합은 1이다.”에 의해 다음과 같이 된다.
\(\sum^n_{k=0}b(k;n,p)=1 \tag{1} \label{eq:binomial sums}\)
또한, 이를 이용해 다음과 같은 이항 분포의 기댓값을 얻을 수 있다.
\(\begin{align}
E[X]&=\sum^n_{k=0}k\cdot \Pr\{X=k\}
\\&=\sum^n_{k=0}k\cdot b(k;n,p)
\\&=\sum^n_{k=1}k\binom{n}{k}p^kq^{n-k}
\\&= np\sum^n_{k=1}\binom{n-1}{k-1}p^{k-1}q^{n-k}
\\&=np\sum^{n-1}_{k=0}\binom{n-1}{k}p^k q^{(n-1)-k}
\\&=np\sum^{n-1}_{k=0}b(k;n-1,p)
\\&=np\ &(식\ \eqref{eq:binomial sums}에\ 의해)
\label{eq:expectation of binomial distribution}
\tag{expectation}
\end{align}\)
또 다른 방법으로 구하려면, 확률 변수 $X_i$를 i 번째 시도에서의 성공 횟수로 가정하면,(즉, 한번 시도했을 때의 성공횟수 => 최대 1 또는 0) $E[X_i]=p\cdot 1+ q\cdot 0=p$가 나오게 된다. 기댓값의 선형성에 의해 아래와 같이 기댓값을 구할 수 있다.
\[\begin{align} E[X]&= E\left[\sum^n_{i=1}X_i\right] \\&=\sum^n_{i=1}E[X_i] \\&=\sum^n_{i=1}p \\&=np \end{align}\]이러한 방법으로 분포의 분산 또한 쉽게 구할 수 있다. 앞선 확률 변수편에서 구했던 분산 공식 $Var[X_i]=E[X_i^2]-E^2[X_i]$에서, 확률 변수 $X_i$는 위에서 언급했듯이 1아니면 0이므로 $X_i^2=X_i$가 되며, 이는 곧 $E[X^2_i]=E[X_i]=p$를 의미한다.
따라서 $Var[X_i]=p-p^2=p(1-p)=pq$를 만족하며, 이를 이용해 아래와 같이 확률 변수 X에 대한 분산을 구할 수 있다.
\[\begin{align} Var[X]&= Var\left[\sum^n_{i=1}X_i\right] \\&=\sum^n_{i=1}Var[X_i] \\&=\sum^n_{i=1}pq \\&=npq \end{align}\]Figure 2에서 보면, 이항 분포는 k가 증가할 수록 증가하는 추세에서, np에 다다르면 감소하게되는데, 이러한 추세는 다음과 같은 연속식의 비율로 증명 가능하다.
\[\begin{align} \frac{b(nk;n,p)}{b(k-1;n,p)}&=\frac{\binom{n}{k}p^kq^{n-k}}{\binom{n}{k-1}p^{k-1}q^{n-k+1}} \\&=\frac{n!(k-1)!(n-k+1)!p}{k!(n-k)!n!q} \\&=\frac{(n-k+1)p}{kq} \\&=1+\frac{(n+1)p-k}{kq} \label{eq:ratio of binomial distribution} \tag{2} \end{align}\]이 비율은 $(n+1)p-k$가 양수일때 1보다 크며, 즉 $b(k;n,p)>b(k-1;n,p)$일때, $k<(n+1)p$, 즉 분포가 증가하는 추세이고, $b(k;n,p)<b(k-1;n,p)$일때, $k>(n+1)p$, 즉 분포가 감소하는 추세이다.
만약 $k=(n+1)p$가 정수라면, $b(k;n,p)=b(k-1;n,p)$이며, k의 범위가 $np-q <k<(n+1)p$일때 최대값을 얻을 수 있다.
이항 분포의 상한을 얻을 수 있는 부명제 증명
부명제 1. $n \geq 0$이고, $0<p<1$ $q=1-p$이며, $0\leq k \leq n$일때, 다음 식이 성립한다.
\(b(k;n,p)\leq (\frac{np}{k})^k(\frac{nq}{n-k})^{n-k}\)
증명:
앞서 Counting 편의 이항 한계의 식에서 배웠던 $\binom{n}{k}\leq \frac{n^n}{k^k(n-k)^{n-k}}$을 통하여 다음이 성립한다.
\(\begin{align}
b(k;n,p)&=\binom{n}{k}p^kq^{n-k}
\\&\leq \left(\frac{n}{k}\right)^k\left(\frac{n}{n-k}\right)^{n-k}p^kq^{n-k}
\\&=\left(\frac{np}{k}\right)^k \left(\frac{np}{n-k}\right)^{n-k}
\end{align}\)
이항 분포의 꼬리들 (The tails of the binomial distribution)
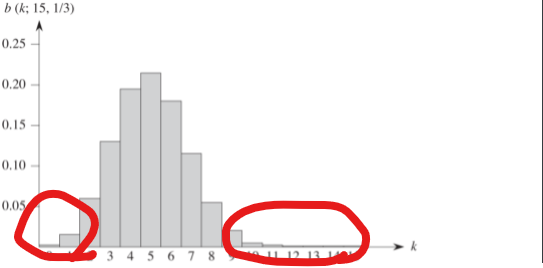
이항 분포의 가장 확률이 높은 지역인 평균($np$)에서 가장 먼 양 끝단을 이항 분포의 꼬리(tail) 부분이라고 하며, 좌측 꼬리는 최소의 성공, 우측 꼬리는 최대의 성공확률를 의미한다.
먼저 분포에서 우측 꼬리의 한계(bound)에 대해 알아보자.
정리(Theorem) 1
n번의 베르누이 시행에서 성공 확률이 p이며, 확률 변수 X가 성공 횟수를 의미할 때, $0\leq k \leq n$일 때, 최소 성공 횟수 k의 확률의 상한은 다음과 같다.
\(\Pr\{X\geq k\}=\sum^n_{i=k}b(i;n,p)\leq \binom{n}{k}p^k\)
증명
$S \subseteq {1,2,\dots,n}$일 때, $A_S$를 $i\in S$인 i번째 시도 하나가 성공인 사건으로 놓으면 $|S|=k$일 때, $\Pr{A_S}=p^k$이게 된다.(모든 시도 중에 S에 속한 i번째 시도가 전부 성공할 확률)
그럴 경우, 아래가 성립한다.
\(\begin{align}
\Pr\{X\geq k\}&=\Pr\{there\ exists\ S\subseteq \{1,2,\dots,n\}:|S|=k\ and\ A_S\}
\\&=\Pr\left\{\bigcup_{S\subseteq\{1,2,\dots,n\}:|S|=k}A_S\right\} & (S에\ 속한\ 모든\ i\ 번째\ 시도가\ 성공할\ 확률)
\\&\le \sum_{S\subseteq\{1,2,\dots,n\}:|S|=k}\Pr\{A_S\} &(Boole 부등식에\ 의해)
\\&=\binom{n}{k}p^k
\end{align}\)
NOTE
부울의 부등식 (Boole’s inequality)
유한 또는 가산 무한 이벤트들의 수열 $A_1, A_2, \dots$에 대하여 확률의 공리 $\Pr{A\cup B}=\Pr{A}+\Pr{B}-\Pr{A\cap B}\leq \Pr{A}+\Pr{B}$$가 만족하므로, \Pr{A_1\cup A_2\cup\cdots}\le \Pr{A_1}+\Pr{A_2}+\cdots$를 만족한다.
따름 정리(Corollary) 2
성공확률이 p이며, n번 시도하는 베르누이 시행에서 확률 변수 X를 성공 횟수로 놓고, $0\leq k \leq n$일 경우, 최대 성공횟수 k에 대한 확률의 상한은 다음과 같다.
이는 또한, 반대편 꼬리에도 적용 가능하다.
\(\begin{align} \Pr\{X\leq k\}&=\sum^k_{k=0}b(i;n,p) \\&\leq \binom{n}{n-k}(1-p)^{n-k} \\&=\binom{n}{k}(1-p)^{n-k} \end{align}\)
정리(Theorem) 3
성공확률이 p이며, 실패 확률이 $q=1-p$인 n번 시도하는 베르누이 시행에서 확률 변수 X를 성공 횟수로 놓고, $0 < k< np$에서 k보다 적게 성공할 확률의 상한은 다음과 같다.
\(\begin{align}
\Pr\{X<k\}&=\sum^{k-1}_{i=0}b(i;n,p)
\\&< \frac{kq}{np-k}b(k;n,p)
\end{align}\)
이는 이항 분포의 좌측 꼬리에 대한 한계이며, 좌측 꼬리부터 기하급수적으로 줄어드는 이유이다.
증명
먼저 수열 $\sum^{k-1}_{i=0}b(i;n,p)$을
연속합편
에서 배웠던 등비수열을 통해 한계를 구한 뒤, $i=1,2,\dots,k,$일 때, 식 $\eqref{eq:ratio of binomial distribution}$를 통해 다음이 성립한다.
\(\begin{align}
\frac{b(i-1;n,p)}{b(i;n,p)}&=\frac{iq}{(n-i+1)p}
\\&<\frac{iq}{(n-i)p}
\\&\leq\frac{kq}{(n-k)p}
\end{align}\)
이때 x를 다음과 같이 정하면, x의 상한을 얻을 수 있다.
\(\begin{align}
x&=\frac{kq}{(n-k)p}
\\&<\frac{kq}{(n-np)p}
\\&=\frac{kq}{nqp}
\\&=\frac{k}{np}
\\&<1
\end{align}\)
위 식을 통해 식 $b(i-1;n,p)<xb(i;n,p)$이 성립하게 된다.
위 부등식을 $0<i\leq k$일 때, k-i번 연속적으로 적용하면 $b(i;n,p)<x^{k-i}b(k;n,p)$를 구할 수 있다.
$0\leq i <k$일 때, 다음이 성립한다.
\(\begin{align}
\sum^{k-1}_{i=0}b(i;n,p)&<\sum^{k-1}_{i=0}x^{k-i}b(k;n,p)
\\&<b(k;n,p)\sum^\infty_{i=0}x^i
\\&=\frac{x}{1-x}b(k;n,p)
\\&=\frac{kq}{np-k}b(k;n,p)
\end{align}\)
따름 정리(Corollary) 4
성공확률이 p이며, 실패 확률이 $q=1-p$인 n번 시도하는 베르누이 시행에서 확률 변수 X를 성공 횟수로 놓고, $0<k\leq np/2$에서 k번 보다 적게 성공할 확률은 k+1번 보다 적게 성공할 확률보다 절반 이하이다.
증명
$k\leq np/2$이기 때문에 다음이 성립한다.
\(\frac{kq}{np-k}\leq \frac{(np/2)q}{np-(np/2)}=\frac{np/2q}{np/2}\leq 1\)
확률 q는 1보다 작으므로, 정리(Theorem) 3과 위의 식에 의해 k보다 적게 성공할 확률은 다음과 같이 된다.
\(\Pr\{X<k\}=\sum^{k-1}_{i=0}b(i;n,p)<b(k;n,p)\)
따라서, $\sum^{k-1}_{i=0}b(i;n,p)<b(k;n,p)$에 의해 다음과 같은 식이 성립한다.
\(\begin{align}
\frac{\Pr\{X<k\}}{\Pr\{X<k+1\}}&=\frac{\sum^{k-1}_{i=0}b(i;n,p)}{\sum^k_{i=0}b(i;n,p)}
\\&=\frac{\sum^{k-1}_{i=0}b(i;n,p)}{\sum^{k-1}_{i=0}b(i;n,p)+b(k;n,p)}
\\&<1/2
\end{align}\)
이는, 다른 반대편 꼬리에도 똑같이 적용된다,즉 k번보다 많게 성공할 확률은 k-1번 보다 많게 성공할 확률의 절반 이하이다. (따름 정리 6 참조)
따름 정리(Corollary) 5
성공확률이 p이며, 실패 확률이 $q=1-p$인 n번 시도하는 베르누이 시행에서 확률 변수 X를 성공 횟수로 놓고, $np<k<n$일 때, k번보다 높게 성공할 확률은 다음과 같은 상한을 가지고 있다.
$\Pr{X>k}=\sum^n_{i=k+1}b(i;n,p)<\frac{(n-k)p}{k-np}b(k;n,p)$
따름 정리(Corollary) 6
성공확률이 p이며, 실패 확률이 $q=1-p$인 n번 시도하는 베르누이 시행에서 확률 변수 X를 성공 횟수로 놓고 $(np+n)/2<k<n$ 를 만족할 때, k보다 많이 성공할 확률은 k-1보다 많이 성공할 확률의 절반 이하이다.
정리 (Theorem) 7
n번의 베르누이 시행에서,$i=1,2,\dots,n$에서 각 i번째 시도의 성공확률을 $p_i$로 놓고, 실패 확률을 $q_i=1-p_i$로 놓는다.
확률 변수 X를 총 성공 횟수로 놓고, $\mu=E[X]$로 놓고, $r>\mu$일 경우, $\Pr{X-\mu \geq r} \leq (\frac{\mu e}{r})^r$가 성립한다.
이 정리를 통해 이항 분포의 우측 꼬리의 한계를 알 수 있다.
증명
$\alpha >0$일 때, 함수 $e^{\alpha x}$는 x에 대해 크기가 비례하게 되므로, 다음이 성립한다.
\[\Pr\{X-\mu \geq r\}=\Pr\{e^{\alpha(X-\mu)}\geq e^{\alpha r}\} \label{eq:possibility bound by markov inequality}\tag{3}\]위 식을 이용해 음이 아닌 확률 변수 X의 확률의 상한을 알 수 있는 마르코프 부등식(Markov’s inequality)에 의하여 $t>0$일 경우, $\Pr{X \geq t}\leq E[X]/t$이 성립하므로 다음 식 $\eqref{eq:possibility bound by markov inequality with exponential}$이 성립한다.
\(\Pr\{e^{\alpha(X-\mu)}\geq e^{\alpha r}\}\leq E[e^{\alpha (X-\mu)}]e^{-\alpha r}
\label{eq:possibility bound by markov inequality with exponential}\tag{4}\)
NOTE
마르코프 부등식(Markov’s inequality)의 증명
\(\begin{align}
E(X)&=\int^\infty_{-\infty}xf(x)dx\ &(기댓값의\ 정의)\\
\\&=\int^\infty_{0}xf(x)dx&(X는\ 음이\ 아닌\ 확률\ 변수이므로)
\\&=\int^a_{0}xf(x)dx+\int^\infty_{a}xf(x)dx
\\&\geq\int^\infty_{a}xf(x)dx
\\&\geq \int^\infty_{a}af(x)dx
\\&=a\int^\infty_{a}f(x)dx
\\&=a\Pr(X\geq a)
\\& \therefore \Pr\{X \geq a\}\leq E[X]/a
\end{align}\)
증명 과정은 $E[e^{\alpha (X-\mu)}]$의 한계 구하기와 식 $\eqref{eq:possibility bound by markov inequality with exponential}$의 $\alpha$값의 적절한 대체가 주를 이룬다.
먼저 지시 확률 변수(indicator random variables)를 이용해 확률 변수 $X_i$를 i번째 베르누이 시행이 성공이면 1, 실패이면 0으로 설정한다. 따라서
$X=\sum^n_{i=1}X_i$가 성립하며,
기댓값의 선형성에 의해 $\mu=E[X]=E\left[\sum^n_{i=1}X_i\right]=\sum^n_{i=1}E[X_i]=\sum^n_{i=1}p_i$이 성립하며 이는 $X-\mu=\sum^n_{i=1}(X_i-p_i)$을 성립하게 한다.
이제 $X-\mu$를 위에 구한 식으로 대체하면, 다음이 성립한다.
\(\begin{align}
E[e^{\alpha(X-\mu)}] &=E[e^{\alpha \sum^n_{i=1}(X_i-p_i)}]
\\&=E\left[\prod^n_{i=1} e^{\alpha(X_i-p_i)}\right]
\\&=\prod^n_{i=1}E[e^{\alpha(X_i-p_i)}]
\end{align}\)
이때 상호 독립적인 확률 변수 $X_i$는 확률변수 $e^{\alpha (X_i-p_i)}$ 또한 상호 독립적으로 만드므로, 기댓값의 정의와 $\alpha >0, q_i\leq 1, e^{\alpha q_i}\leq e^\alpha,e^{-\alpha p_i}\leq 1, e^x \ge 1+x$등의 부등식들에 의해 다음이 성립한다.
\(\begin{align}
E[e^{\alpha(X_i-p_i)}] &= e^{\alpha(1-p_i)}p_i+e^{\alpha(0-p_i)}q_i
\\&= p_ie^{\alpha q_i}+q_ie^{-\alpha p_i}
\\&\leq p_ie^\alpha+1
\\&\leq \exp(p_ie^\alpha)
\end{align}\)
여기서 $\exp(x)=e^x$는 지수함수를 의미한다.
따라서 $\mu =\sum^n_{i=1}p_i$이므로, 다음이 성립하며,
\(\begin{align}
E[e^{\alpha(X-\mu)}] &= \prod^n_{i=1}E[e^{\alpha(X_i-p_i)}]
\\&\leq \prod^n_{i=1}\exp(p_ie^\alpha)
\\&= \exp\left(\sum_{i=1}^n p_ie^\alpha\right)
\\&= \exp(\mu e^\alpha)
\label{eq:Expectation to exp func}
\tag{5}
\end{align}\)
식 $\refeq{eq:possibility bound by markov inequality}$, 식 $\refeq{eq:possibility bound by markov inequality with exponential}$, 식 $\refeq{eq:Expectation to exp func}$에 의해 다음이 성립한다.
이때, $\alpha =\ln(r/\mu)$로 대입하면 다음과 같은 식이 나온다.
\[\begin{align} \Pr\{X-\mu \geq r\} &\leq \exp(\mu e^{\ln(r/\mu)}-r\ln(r/\mu)) \\&=\exp(r-r\ln(r/\mu)) \\&= \frac{e^r}{(r/\mu)^r} \\&= (\frac{\mu e}{r})^r \end{align}\]따름 정리(Corollary) 8
언제나 같은 확률인 베르누이 시행에서는 이항 분포의 우측 꼬리에서 다음이 성립한다.
성공확률이 p이며, 실패 확률이 $q=1-p$인 n번 시도하는 베르누이 시행에서 $r > np$일 때, 다음이 성립한다.
\(\Pr\{X-np\geq r\}=\sum^n_{k=\lceil np+r \rceil}b(k;n,p)=(\frac{npe}{r})^r\)
증명
이항 분포의 기댓값을 유도하는 식 $\refeq{eq:expectation of binomial distribution}$에 의해 $\mu= E[X]=np$이 성립한다.
_articles/computer_science/algorithm/MATH/알고리즘 수학 기본-기하, 이항 분포.md