알고리즘 수학 기본-유한합

Jul 11, 2021

알고리즘을 위한 수학 - 유한합(Summation)

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.

유한합 (Summations)

유한합은 while이나 for 루프가 존재하는 알고리즘의 시간 복잡도를 계산하는데 사용할 수 있다.

때문에, 시그마($\sum$)으로 표현되는 유한합에 대해서 알 필요가 있다. 이 책에서는 대다수의 공식의 증명은 생략되어 있다.

유한합 공식과 성질(Summation formulas and properties)

n이 유한한 양의 정수이고, n개의 숫자들 $a_1,a_2,\cdots, a_n$이 존재할 때, 이들 모두의 합 $a_1+a_2+\cdots +a_n$은 다음과 같이 표현될 수 있다.
\(\begin{equation} \sum^n_{k=1}a_k \label{eq:sigmaBasic} \tag{A.1} \end{equation}\)
이를 유한급수(finite series)라고 하며, 만약 n이 0이면, 식 $\eqref{eq:sigmaBasic}$의 값은 0이다.

만약, n이 무한하고, 무한한 숫자들 $a_1,a_2,\cdots$를 모두 더한다면 $\sum^\infty_{k=1}a_k$로 표현되며, 이는 다음과 같이 극한값으로 해석될 수 있다.
\(\lim_{n\rightarrow\infty}\sum^n_{k=1}a_k\)
이를 무한급수(infinite series)라고 하며, 어떠한 값에 한없이 가까워지는 수렴 급수(convergent series)와 그렇지 않은 발산 급수(divergent series)로 나뉜다.

이때, 각 항 $a_k$에 절대값을 취한 항 $\left

a_k\right

$들의 합, 또는 절대수렴(absolute convergence) 급수가 수렴할 경우, 원래의 수렴급수들의 합 $\eqref{eq:sigmaBasic}$ 또한 수렴한다.

• 절대수렴 급수들은 기존의 수렴 급수와 달리 합의 순서가 바뀌어도 결과값이 변하지 않는다.

선형성(Linearity)

어떠한 실수 c와 어떠한 유한한 양의 정수 n으로 이루어진 두 급수 $a_1,a_2,\cdots,a_n$과 $b_1,b_2,\cdots,b_n$이 주어졌을때 다음과 같은 식이 성립한다.
\(\sum^n_{k=1}(ca_k+b_k)=c\sum^n_{k=1}a_k+\sum^n_{k=1}b_k\)
이러한 선형성 설질은 무한수렴급수에도 적용되며, 이를 통해 점근적 표기법을 사용하는 유한합을 조작할 수 있는데 예를 들자면, 다음 식 $\eqref{eq:sigmaTheta}$이 성립한다.
\(\begin{equation} \sum^n_{k=1}\Theta(f(k))=\Theta\left( \sum^n_{k=1}f(k)\right) \label{eq:sigmaTheta} \tag{A.2} \end{equation}\)
다음 식 $\eqref{eq:sigmaTheta}$의 좌측 항의 $\Theta$ 표기는 변수 k에 대해서이며, 우측항은 변수 n에 대한 표기이다. 이 또한 무한 수렴 급수에 적용된다.

등차 수열(Arithmetic series)

유한합 $\sum^n_{k=1}k=1+2+\cdots+n$를 등차 수열(arithmetic series)이라고 하며, 다음과 같은 값을 가진다.

\[\begin{align}\sum^n_{k=1}k &=\frac{1}{2}n(n+1) \label{eq:sigmaArtithSum} \tag{A.3} \\&=\Theta(n^2) \label{eq:sigmaArithSumTheta} \tag{A.4} \end{align}\]

제곱과 세제곱의 합(Sums of squares and cubes)

\[\begin{align} &\sum^n_{k=0}k^2=\frac{n(n+1)(2n+1)}{6}\label{eq:sigmaSquareSum}\tag{A.5}\\ &\sum^n_{k=0}k^3=\frac{n^2(n+1)^2}{4}\label{eq:sigmaCubeSum}\tag{A.6} \end{align}\]

제곱과 세제곱 급수들의 합에 대한 유한합의 공식

등비 수열 또는 기하수열(Geometric Series or Exponential Series)

실수 $x$가 1이 아닌 급수들을 등비수열 또는 기하수열이라고 표현하며, 등비수열의 합은 다음과 같이 표현할 수 있다.
\(\sum^n_{k=0}x^k=1+x+x^2+\cdots+x^n\)
등비수열의 합과 무한급수 등비수열의 합은 다음과 같은 공식으로 표현될 수 있다.
\(\begin{align} &\sum^n_{k=0}x^k=\frac{x^{n+1}-1}{x-1} \label{eq:sigmaGemetSum} \tag{A.7}\\ &\sum^\infty_{k=0}x^k=\frac{1}{1-x},\ when\ \left|x\right|<1 \label{eq:sigmaGemetSumInf} \tag{A.8} \end{align}\)

조화수열 (Harmonic Series)

양의 정수 n에 대하여 n개의 조화수열은 아래와 같은 식으로 표현된다.

\[\begin{align} H_n&=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n}\\&=\sum^n_{k=1}\frac{1}{k}\\&=\ln n+O(1) \label{eq:sigmaHarmonSum} \tag{A.9} \end{align}\]

자세한 증명은 아래 유한합 나누기(Splitting summations) 파트에서 보여준다.

수열 합의 적분과 미분(Integrating and differentiating series)

기존의 공식에 양 항을 적분 또는 미분하는 것으로 새로운 공식을 얻을 수 있다. 예를 들면 식 $\eqref{eq:sigmaGemetSumInf}$의 양 항을 미분한 뒤, $x$를 곱하면 다음과 같은 식이 나온다.
\(\sum^\infty_{k=0}kx^k=\frac{x}{(1-x)^2}\ when\ \left | x \right | < 1.\label{eq:sigmaGeometSumDiff}\tag{A.10}\)

망원수열(Telescoping Series)

모든 수열에 대하여 다음 식이 성립하며, 이러한 부분적 항들의 합이 소거 후, 일부 고정된 값만 남는 수열을 망원 수열이라 한다.
\(\sum^n_{k=1}(a_k-a_{k-1})=a_n-a_0 \label{eq:sumTeleScope} \tag {A.11}\)
위를 응용하여 두 가지 변형 공식을 얻을 수 있는데, 첫번째는
\(\sum^{n-1}_{k=0}(a_k-a_{k+1})=a_0-a_n\)
또한, 다음과 같은 식이 성립하는데,
\(\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}\)
이를 통해 아래와 같은 두번째 공식을 얻을 수 있다.
\(\sum^{n-1}_{k=1}\frac{1}{k(k+1)}=\sum^{n-1}_{k=1}\left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n}\)

곱 (Products)

우리는 유한한 양의 정수 n에 대하여 수열 $a_1, a_2, \cdots, a_n$의 곱 $a_1a_2\cdots a_n$를 아래와 같이 표현한다.

\[\prod^n_{k=1}a_k\]

이때 n이 0일때의 곱의 값은 1이다. 이러한 공식은 다음과 같은 유한합 공식과 연결될 수 있다.
\(\lg\left(\prod^n_{k=1}a_k\right)=\sum^n_{k=1}\lg a_k \label{eq:prodToLogSum} \tag{A.12}\)

유한합의 범위 제한(Bounding summations)

수열의 합의 범위를 앎으로써, 알고리즘의 비용에 대해 알 수 있으므로, 유한합의 범위를 제한하는 여러가지 방법에 대해 알아보자.

수학적 귀납법(Mathematical induction)

수학적 귀납법은 가장 쉽고 빠른 방법이다.

수학적 귀납법은 어떠한 자연수가 특정 조건을 만족하고, 다음 자연수 또한 만족한다는 것을 증명하면, 모든 자연수가 해당 조건을 만족한다는 증명이다.

예를 들어, $\sum^n_{k=1}k = \frac{1}{2}n(n+1)$가 참임을 증명하려면, 먼저 n = 1일 경우, 성립된다는 것은 $\frac{1}{2}\cdot 1(1+1)=1$임으로 자명하며, 이제 $\sum^{n+1}_{k=1}k$의 값을 구한 뒤, $m = n+1$으로 놓는다면, 다음과 같은 식이 성립한다.
\(\begin{align} \sum^{n+1}_{k=1}k=&\sum^n_{k=1}k+(n+1) \\&=\frac{1}{2}n(n+1)+(n+1) \\&=\frac{1}{2}(n+1)(n+2) \\&=\frac{1}{2}m(m+1) \end{align}\)

이는 기존의 $\frac{1}{2}n(n+1)$와 같은 꼴이므로, 가정이 n에 대해 성립하고, n+1에 대해 성립함을 보였으니 $\sum^n_{k=1}k = \frac{1}{2}n(n+1)$은 참이다.

또한, 수학적 귀납법을 통해 유한합의 범위(bound)를 증명할 수도 있다.

예를 들어, $\sum^n_{k=0}3^k$가 $O(3^n)$, 즉 상수 c에 대해 $\sum^n_{k=0}3^k \leq c3^n$임을 증명해볼 수 있다.

먼저 n이 0일때, $\sum^0_{k=0}3^k = 1 \leq c\cdot 1$ 이므로 가정이 참임을 알 수 있고, n+1의 경우 다음과 같이 증명된다.
\(\begin{align} \sum^{n+1}_{k=0}3^k=&\sum^n_{k=0}3^k+3^{(n+1)} \\&\leq c3^n+3^{n+1}\ (귀납적\ 가정에의해) \\&=\left(\frac{1}{3}+\frac{1}{c}\right)c3^{n+1} \\&\leq c3^{n+1} \end{align}\)

즉 $(1/3+1/c)\leq 1$, $c \geq 3/2$인 경우에 성립하므로, $\sum^n_{k=0}3^k = O(3^n)$이다.

단, 아래 예시처럼 귀납적 방법으로 증명하며 점근 표기법을 사용할 때 주의해야 한다.

예를 들어 $\sum^{n}{k=1}k = O(n)$임을 증명할 때, $\sum^{1}{k=1}k = O(1)$이므로, 아래와 같이 $\sum^{n}_{k=1}k = O(n)$으로 놓는 것은 옳지 않다.
\(\begin{align} \sum^{n+1}_{k=1}k&=\sum^n_{k=1}k+(n+1) \\&=O(n)+(n+1) \Leftarrow 틀림. \\&=O(n+1) \end{align}\)

이때는 k가 1일 때 뿐만 아니라 모든 n에 대해 성립됨을 보여야 $\sum^{n}_{k=1}k = O(n)$이 된다.

항들의 한계값 (Bounding the terms)

수열의 각 항들의 상한(upper bound)들을 통하여 수열합의 상한을 구할 수도 있다.

예를 들어 식 $\eqref{eq:sigmaArtithSum}$을 통해 상한(upper bound)을 통해 아래와 같은 식이 성립된다.
\(\sum^n_{k=1}k\leq \sum^n_{k=1}n=n^2\)

또한, 각 항 중에 최대값인 항을 이용하는 방법은 다음과 같다.

$a_1,a_2,\cdots, a_n$ 까지의 수열 중 최대 값을 $a_{max}$라고 할 때, 다음과 같은 식이 성립된다.

• 수열에서 가장 큰 값의 n배가 모든 n개의 수열의 합보다 크다는 의미.

\[\sum^n_{k=1}a_k\leq n\cdot a_{max}\]

위처럼 최대값 항을 이용하는 방법은 등비 수열에서는 적합하지 않은 경우가 많으며, 대신 다음과 같이 무한 감소 등비 수열(infinite decreasing geometric series)과 최대값 항을 같이 이용할 수 있다.

등비수열 $\sum^n_{k=0}a_k$에 대하여 $a_{k+1}/a_k \leq r$이며, $0<r<1$일 때(즉, 점점 일정 비율로 감소하는 등비 수열), 다음이 성립한다.
\(a_k\leq a_0r^k\)
이를 이용하면 다음과 같은 식이 성립한다.
\(\begin{align} \sum^n_{k=0}a_k&\leq \sum^{\infty}_{k=0}a_0r^k \\&=a_0\sum^{\infty}_{k=0}r^k \\&=a_0\frac{1}{1-r} \tag{A.13} \label{eq:boundGeometSum} \end{align}\)

위의 식 $\eqref{eq:boundGeometSum}$을 이용해 $\sum^{\infty}_{k=1}\frac{k}{3^k}$의 상한을 알아보자.

$\sum^{\infty}{k=1}k/3^k$를 k가 0부터 시작하는 수열합으로 바꾸면 $\sum^{\infty}{k=0}(k+1)/3^{k+1}$가 되며, 이때 첫번째 항($a_0$)는 1/3이며, 각 항 사이의 비율($a_{k+1}/a_{k}$)은 다음과 같다.
\(\frac{(k+2)/3^{k+2}}{(k+1)/3^{k+1}}=\frac{1}{3}\cdot\frac{k+2}{k+1}\leq \frac{2}{3}\)

즉, 식 $\eqref{eq:boundGeometSum}$의 항에서 $r=2/3,\ a_0=1/3$인 경우이므로, k가 0 이상일 경우 다음이 성립한다.
\(\begin{align} \sum^{\infty}_{k=1}\frac{k}{3^k}&=\sum^{\infty}_{k=0}\frac{k+1}{3^{k+1}} \\&\leq \frac{1}{3}\cdot\frac{1}{1-2/3} \\&= 1 \end{align}\)

이때 주의할 점은, 등비수열이 아니며, 무한급수가 수렴하지 않는 경우에서의 증명이다.

예를 들어 아래와 같은 무한 발산 조화 수열의 경우, $k/k+1 < 1$이지만, 무한 등비 수열 처럼 수렴하는 상한이 존재하지 않는다.

\[\begin{align} \sum^{\infty}_{k=1}\frac{1}{k}&=\lim_{n\rightarrow \infty}\sum^n_{k=1}\frac{1}{n} \\&=\lim_{n\rightarrow \infty}\Theta(\lg n) \\&=\infty \end{align}\]

위의 방법으로 경계를 구하기 위해서는 언제나 $r<1$이며, 일정한 상수임을 보여야 한다. 하지만 위의 조화수열의 경우는 k값이 증가하면서 점점 r 값이 1에 가까워지며 변한다.

유한합 나누기 (Splitting summations)

범위를 구하기 힘든 유한합의 경우 2개 이상의 수열로 나누어 볼 수 있다. 예를 들어, $\sum^n_{k=1}k$의 하한(lower bound)를 알아보기 위해, 본능적으로, $\sum^n_{k=1}k$의 수열의 최소값 경계는 n 임을 직감하겠지만 (n이 1인 경우, 수열의 합이 1이므로), 수열을 나누어 구하는 경우를 알아보자.

일단 편의를 위해 아래의 식은 n이 짝수로 가정하면, 다음과 같이 중간값의 수열 두 개로 나눌 수 있다.

• 홀수인 경우에는 n/2 대신 n을 2로 나누는 값의 몫을 기준으로 나누면 같은 결과가 나올 것이다.

\[\begin{align} \sum^n_{k=1}k&=\sum^{n/2}_{k=1}k+\sum^n_{k=n/2+1}k\\ &\geq\sum^{n/2}_{k=1}0+\sum^n_{k=n/2+1}(n/2)\\ &=(n/2)^2=\Omega(n^2)\\ \end{align}\]

$\sum^n_{k=1}k$의 점근적 상한(upper bound)이 $O(n^2)$이므로, 최솟값 경계와 최대값 경계가 거의 동일할 정도로 비슷하다는 것을 알 수 있다.

또한, 수열의 일부분을 상수로 취급하여 지운 뒤, 수열 합 범위를 구할 수 있다.

예를 들어 $k_0 > 0$일 때, $\sum^{k_0-1}{k=0}a_k$를 $\Theta (1)$로 처리하고, $\sum^n{k=k_0}a_k$를 구하여 하한을 구할 수 있을 것이다.

\[\begin{align} \sum^n_{k=0}a_k&=\sum^{k_0-1}_{k=0}a_k+\sum^n_{k=k_0}a_k \\&=\Theta(1)+\sum^n_{k=k_0}a_k \end{align}\]

이러한 방법은 무한 급수의 범위를 찾는데도 사용할 수 있다.

예를 들어 $\sum^\infty_{k=0}\frac{k^2}{2^k}$에서는 한 항목과 다음 항목의 비율 $r =\frac{(k+1)^2/2^{k+1}}{k^2/2^k}$은 값이 0에 가까울 수록 큰데, (정수로 제한할 시, k = 1에서 r = 2),

$\sum^\infty_{k=3}\frac{k^2}{2^k}$에서의 r은 8/9보다 언제나 작게 된다.

\[k \geq 3,\ \frac{(k+1)^2/2^{k+1}}{k^2/2^k}=\frac{(k+1)^2}{2k^2}\leq \frac{8}{9}\]

이를 이용해 다음과 같이 첫번째 수열은 상수 개의 항, 두번째 수열은 감소하는 등비 수열로 만들어 보면, 무한급수 $\sum^\infty_{k=0}\frac{k^2}{2^k}$의 상한의 경우에, 상수에 점근한다는 것을 알 수 있다. (실제로 6에 수렴)

\[\begin{align} \sum^\infty_{k=0}\frac{k^2}{2^k}&=\sum^2_{k=0}\frac{k^2}{2^k}+\sum^{\infty}_{k=3}\frac{k^2}{2^k} \\&\leq\sum^2_{k=0}\frac{k^2}{2^k}+\sum^{\infty}_{k=0}\frac{3^2}{2^3}\left(\frac{8}{9}\right)^k \\&=\sum^2_{k=0}\frac{k^2}{2^k}+\frac{9}{8}\sum^{\infty}_{k=0}\left(\frac{8}{9}\right)^k \\&=O(1) \end{align}\]

다음과 같이 더욱 난해한 조화 수열 또한 점근 한계(asymptotic bounds)를 구할 수 있다.

예를 들어 $H_n=\sum^n_{k=1}\frac{1}{k}$의 점근 한계 $O(\lg n)$은 식 $\eqref{eq:sigmaHarmonSum}$처럼 유도하려면, 먼저 1부터 n까지를 $\lfloor \lg n\rfloor + 1$개의 부분으로 나누고, 각 부분항들의 합의 상한을 1 이하로 맞춘다.

식 $\eqref{eq:sumHarmonProof}$의 첫번재 줄이 성립하는 이유는, $\lfloor\lg n \rfloor$가 2의 제곱수가 아니면 마지막 $\lfloor\lg n \rfloor$번째 부분항들 중, 원본 조화수열에 없는 항들이 포함되기 때문이다.

• 예를 들어 n이 9일때, 원본 조화수열에는 맨 마지막 항이 1/9이지만, 첫번재 줄의 경우 1/10~1/15까지가 더 더해지므로, 원본 조화수열 합보다 커진다.

\[\begin{align} \sum^n_{k=1}\frac{1}{k} &\leq \sum_{i=0}^{\lfloor\lg n\rfloor}\sum_{j=0}^{2^i-1}\frac{1}{2^i+j} \\&\leq \sum_{i=0}^{\lfloor\lg n\rfloor}\sum_{j=0}^{2^i-1}\frac{1}{2^i} \\&=\sum^{\lfloor\lg n \rfloor}_{i=0}1 \\&\leq \lg n + 1 \label{eq:sumHarmonProof} \tag{A.14} \end{align}\]

적분에 의한 근사 (Approximation by integrals)

만약 함수 $f(x)$가 일방적으로 증가하는 경향이라면 적분을 통해 다음과 같은 근사를 할 수 있다.

\[\begin{align} \int^n_{m-1}f(x)dx\leq \sum^n_{k=m}f(k)\leq \int^{n+1}_m f(x)dx \label{eq:inteApproxIncFunc} \tag{A.15} \end{align}\]

아래에 나타나 있는 Figure A.1은 위 식 $\eqref{eq:inteApproxIncFunc}$을 나타낸다. 수열합은 표의 사각형 지역으로 나타나 있으며, 적분 공간은 곡선 아래의 어두운 부분이다.

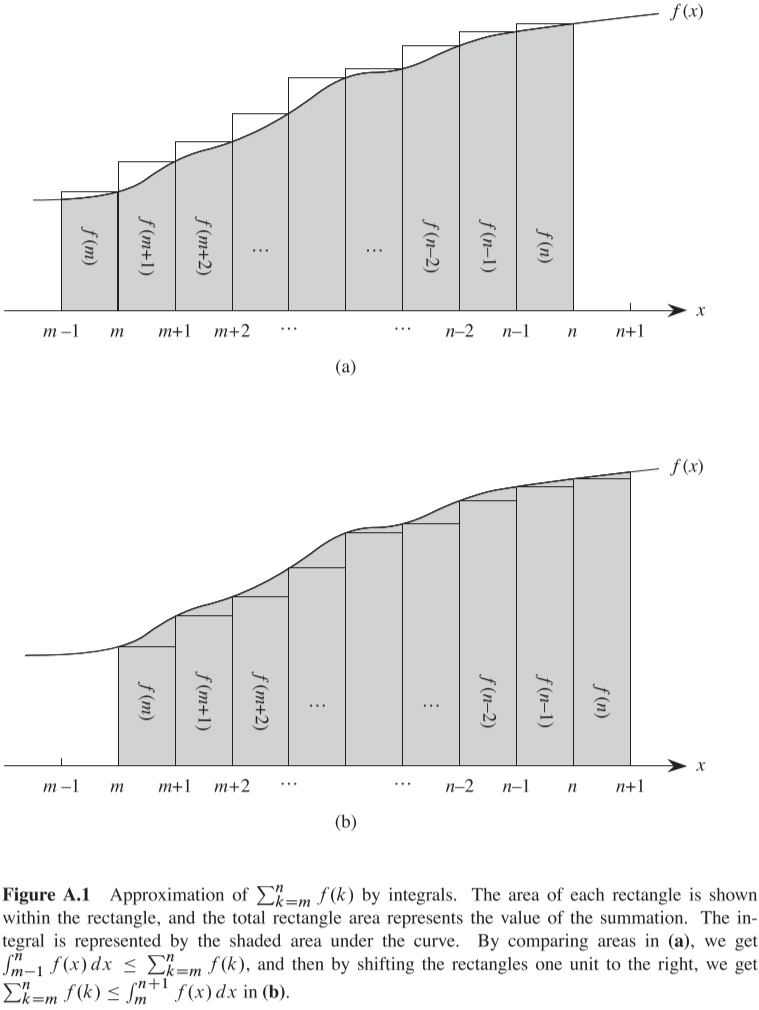
반대로 함수 $f(x)$가 일방적으로 감소하는 경향이라면 다음과 같이 근사할 수 있다.
\(\begin{align} \int^{n+1}_{m}f(x)dx\leq \sum^n_{k=m}f(k)\leq \int^{n}_{m-1} f(x)dx \label{eq:inteApproxDecFunc} \tag{A.16} \end{align}\)

식 $\eqref{eq:inteApproxDecFunc}$을 이용해 n번째 조화수열의 항의 근사값을 구할 수 있다.

먼저 1부터 n까지의 조화수열 합의 하한을 다음과 같이 구한 뒤,

\[\sum^n_{k=1}\frac{1}{k} &\geq \int^{n+1}_1 \frac{dx}{x} \\&= \ln (n+1) \label{eq:inteApprox3} \tag{A.17}\]

2부터 n까지의 조화수열 합의 상한을 다음과 같이 구하면,

\[\sum^n_{k=2} \frac{1}{k} \leq \int^n_1 \frac{dx}{x}= \ln n\]

이를 통해 조화수열의 상한 값을 다음과 같이 구할 수 있다.

\[\sum^n_{k=1} \frac{1}{k} \leq \ln n + 1 \label{eq:inteApprox4} \tag{A.18}\]