알고리즘 수학 기본-확률 변수

Jul 10, 2021

1. 확률 변수(random variables)
   • 이산 확률 변수와 연속 확률 변수(discrete random variables and continuous random variables)
   • 확률 질량 함수와 확률 밀도 함수(Probability Mass Function and Probability Density Function)
   • 확률 변수의 기대값 (Expected value of a random variable)
   • 기대값의 선형성(linearity of expectation)
   • 확산과 표준 편차 (Variance and standard deviation)

알고리즘을 위한 수학 - 확률 변수(random variables)

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.

추가로 _존이(mykepzzang)님의 블로그(https://blog.naver.com/PostList.naver?blogId=mykepzzang)_에서 내용을 발췌하였다.

이 장에서는 확률의 표기법, 정의, 속성 같은 기본적인 것만 배운다.

들어가기에 앞서 확률에 대한 기본적인 이해가 필요하므로 알고리즘을 위한 수학 -확률편을 보고 오는 것을 추천한다.

---

확률 변수(random variables)

이산 확률 변수와 연속 확률 변수(discrete random variables and continuous random variables)

확률 변수는 표본 공간의 각 원소사건을 특정 실수에 대응시켜 확률이 나오게 하는 함수이다.

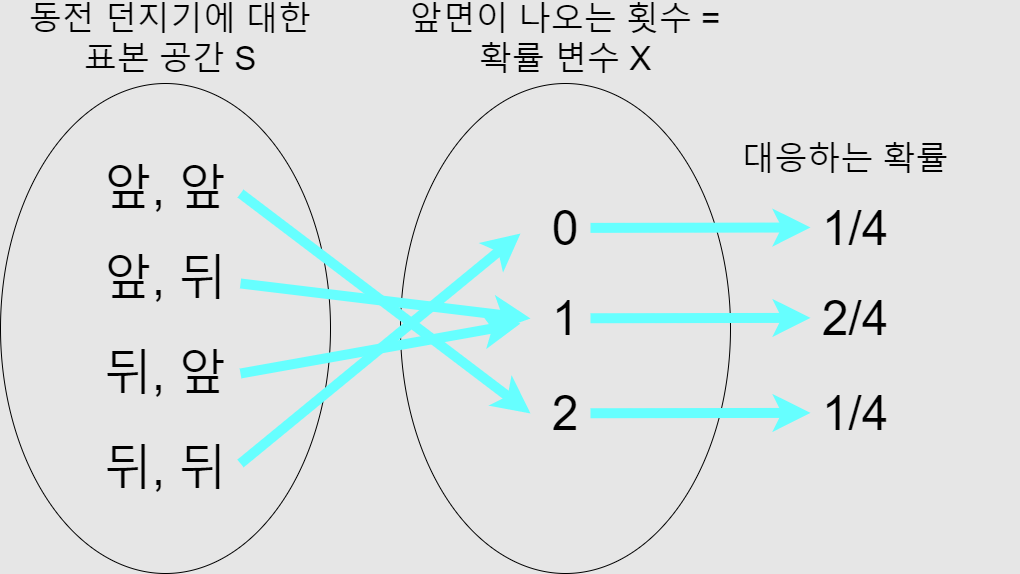
예를 들어, 동전 두개를 던져, 앞면이 2개 나올 확률은 1/4, 앞면 1개, 뒷면 1개가 나올 확률은 1/2, 뒷면 2개가 나올 확률은 1/4가 된다.

이때, 앞면의 갯수는 앞에서 부터 2개,1개,0개가 되는데, 이를 확률 변수로 이용할 수 있다.

즉 앞면의 갯수 확률 변수 X 0, 1, 2에 따라 다음과 같다.
\(P(X=0)=1/4\\ P(X=1)=1/2\\ P(X=2)=1/4\)
확률변수는 가능한 결과에 대한 실수값을 할당하여 이를 통해 확률 분포를 유도할 수 있게 해준다.

이산 확률 변수(Discrete random variables) X는 유한 또는 가산 무한 표본 공간 S를 입력으로 받아, 실수를 출력하는 함수이다.

연속 확률 변수(Continuous random variables) X는 적분을 이용하여, 불가산 무한 표본 공간에도 확률 변수를 이용할 수 있게 한 함수이다.

확률 질량 함수와 확률 밀도 함수(Probability Mass Function and Probability Density Function)

확률 변수 X와 실수 x 에 대해 사건 X=x를 ${s \in S : X(s)=x}$로 정의할 때, 다음과 같이 표현할 수 있다.
\(\begin{align} &이산\ 확률\ 변수의\ 확률\ 질량\ 함수 :\\ &\Pr\{X=x\}=\sum_{s\in S:X(s)=x}\Pr\{s\}\\ &연속\ 확률\ 변수의\ 확률\ 밀도\ 함수 :\\ &\Pr\{X=x\}=\int_{-\infty}^\infty \Pr\{s\} \end{align}\)
이때, 이산 확률 변수 X에 관한 확률의 함수 $f(x)=\Pr{X=x}$를 확률 질량 함수(probability Mass Function) Pr(X)이라고 한다.

위의 예시에서는 $P(X)={}_2 C_x\cdot(1/2)^x(1/2)^{2-x}={}_2 C_x \cdot (1/4)$이 될 것이다.

연속 확률 변수 처럼 연속적인 공간에서는 확률 질량 함수가 아닌 확률 변수 X에 대한 확률 밀도 함수(probability density function)라고 부르며,

확률 질량 함수와 확률 밀도 함수 둘다 확률 정리에 의해 $\Pr{X=x}\geq 0$이며, $\sum_x\Pr{X=x}=1$이다.

예를 들어, 두개의 6면 주사위의 결과 실험은 표본 공간 내에서 6 * 6, 총 36개의 근원 사건으로 이루어져 있다. 확률 분포가 균등하다고 가정하면, 각 근원 사건 $s\in S$의 확률은 정확히 $\Pr{s}=1/36$이 된다.

확률 변수 X를 “주사위 두 값 중의 최댓값”이라고 정의하면, $\Pr{X=3}=5/36$이 되는데, 최대값이 3이 되는 방법은 (1,3), (2,3), (3,3), (3,2), (3,1) 총 5가지이기 때문이다.

여러개의 확률 변수를 이용할 수도 있다. 확률 변수 X, Y에 대해 함수 $f(x,y)=\Pr{X=x\ and\ Y=y}$를 X와 Y의 결합 확률 밀도 함수(joint probability density function)라고 한다.

고정된 값 x, y에 대하여 각각 식 $\Pr{X=x}=\sum_y\Pr{X=x\ and\ Y=y}$과 식 $\Pr{Y=y}=\sum_x\Pr{X=x\ and\ Y=y}$이 성립하며, 확률 편에서 배웠던 조건부 확률의 정의를 이용해 식 $\Pr{X=x

Y=y}=\frac{\Pr{X=x\ and\ Y= y}}{\Pr{Y=y}}$을 얻을 수 있다.

모든 x와 y에 대해 사건 X=x와 Y=y은 독립적이라 가정하면 두 확률 변수 X와 Y가 서로 독립적이며,

만약 모든 x와 y에 대해 식 $\Pr{X=x\ and\ Y=y}=\Pr{X=x}\Pr{ Y=y}$이 성립한다면 두 확률 변수 X와 Y는 서로 동일하다는 의미이다.

동일한 표본 공간에 정의된 여러 확률 변수의 집합으로 곱, 합, 또는 다른 함수를 통해 새로운 확률 변수들을 정의할 수 있다.

확률 변수의 기대값 (Expected value of a random variable)

확률 변수의 분산을 가장 간단하고 유용하게 요약하는 방법은 바로 값들의 평균을 취하는 것이다.

이산 확률 변수 X에 대해 기대값(expected value), 기대치(expactation), 혹은 평균(mean)은 다음 식과 같다.
\(이산 확률 변수의\ 기대값 : \\E[X]=\sum_x x\cdot\Pr\{X=x\}\tag{1}\label{eq:expected value of discrete random variable X}\)
이 식은 예상치가 수렴 또는 유한할 때, 적합하며 $\mu_x$ 또는 $\mu$라고 표기한다.

확률 변수 X의 확률분포함수가 $f(x)=\Pr{X=x}$일 때, 연속 확률 변수의 기대값은 아래와 같다.
\(\begin{align} \\&연속 확률 변수의\ 기대값: \\&E(X)=\int^\infty_{-\infty}x\cdot \Pr\{X=x\}dx \end{align}\)
앞면(H) 하나당 3달러를 얻고 뒷면(T) 하나당 2달러를 잃는 동전을 두개 튕기는 게임에서 확률 변수 X의 기대값은 다음과 같은 방법으로 구한다.
\(\begin{align} E[X]&=6\cdot\Pr\{2\small{H}'s\}+1\cdot\Pr\{1\small{H},1\small{T}\}-4\cdot \Pr\{2\small{T}'s\}\\ &=6(1/4)+1(1/2)-4(1/4)\\ &=1\\ \end{align}\)

기대값의 선형성(linearity of expectation)

두 확률 변수의 합의 기대값은 두 예상치의 합과 같으며, 이는 다음과 같은 식으로 표현된다.

$1.\ E[X+Y]=E[X]+E[Y]$

이를 연속 확률 변수의 기대값의 정의를 이용해 증명하자면 다음과 같다.
\(\begin{align} E(X+Y)&=\int^\infty_{-\infty}\int^\infty_{-\infty}(x+y)\cdot f(x,y)\ dxdy \\&=\int^\infty_{-\infty}\int^\infty_{-\infty}x\cdot f(x,y)+y\cdot f(x,y)\ dxdy \\&=\int^\infty_{-\infty}\int^\infty_{-\infty}x\cdot f(x,y)\ dxdy+\int^\infty_{-\infty}\int^\infty_{-\infty}y\cdot f(x,y)\ dxdy \\&=E(X)+E(Y) \end{align}\)
이외에도 확률 변수를 이용하여 아래와 같은 다른 성질들을 증명 할 수 있다.
\(\begin{align} &2.\ E(aX+b)=aE(X)+b\\ &3.\ E(XY)=E(X)E(Y)\\ &4.\ E(aX^2+bX+c)=aE(X^2)+bE(X)+c\\ &5.\ E(aX+bY)=aE(X)+bE(Y) \end{align}\)
모든 확률 변수 X에 대해, 함수 g(x)가 새로운 확률 변수 g(X)를 정의할 수 있고, g(X)의 기대값이 정의될 수 있다면, 아래와 같은 식이 성립된다.
\(E[g(X)]=\sum_xg(x)\cdot \Pr\{X=x\}\)
이때 $g(x)=ax$로 놓고, a를 상수로 본다면, $E[aX]=aE[X]$가 성립된다.

결과적으로 기대값은 선형이며, 식 $E[aX+Y]=aE[X]+E[Y]$ 또한 성립된다.

만약 두 확률 변수 X와 Y가 서로 독립적이고 정의된 기대값이 존재한다면, 아래와 같은 결과가 나온다.
\(\begin{align} E[XY]&=\sum_x\sum_yxy\cdot\Pr\{X=x\ and\ Y=y\}\\ &=\sum_x\sum_yxy\cdot \Pr\{X=x\}\Pr\{Y=y\}\\ &=\left(\sum_xx\cdot\Pr\{X=x\}\right)\left(\sum_yy\cdot\Pr\{Y=y\}\right)\\ &=E[X]E[Y] \end{align}\)
보통, n개의 확률 변수 $X_1,X_2,\dots,X_n$가 상호 독립적이라면, 선형성에 의해 아래 같은 식이 성립한다.

$E[X_1X_2\cdots X_n]=E[X_1]E[X_2]\cdots E[X_n]$

이러한 성질을 기대값의 선형성(linearity of expectation)이라고 하며, X와 Y가 서로 독립적이지 않아도 성립하며, 유한 또는 완전 수렴하는 기대값의 유한합에도 성립한다.

기대값의 선형성은 지시 확률 변수(indicator random variables)를 이용한 확률적 분석을 하는데 중요한 역할을 한다.

• 지시 확률 변수 : 어떤 사건이 일어나면 1 아니면 0이 되는 함수, 자세한 이야기는 이곳에서 하지 않는다.

확률 변수 X가 값이 자연수 집합 $\N={0,1,2,\dots}$에 속한다면, 다음과 같은 기대값에 대한 식을 사용할 수 있다.
\(\begin{align} E[X]&=\sum_{i=0}^\infty i\cdot\Pr\{X=i\}\\ &=\sum_{i=0}^\infty i(\Pr\{X\geq i\}-\Pr\{X\geq i+1\})\\ &=\sum_{i=1}^\infty \Pr\{X\geq i\} \end{align} \tag{2} \label{eq: expectation on natural numbers}\)
볼록 함수(convex function) $f(x)$를 확률 변수 X에 적용하며, 옌센 부등식(Jensen’s inequality)을 통해 다음과 같은 식을 얻을 수 있다.

$E[f(X)]\geq f(E[X])$

• 옌센 부등식(Jensen’s inequality) : 기댓값의 볼록함수와 볼록 함수의 기댓값 사이에 성립하는 부등식

이 식을 통해 기대값의 존재와 유한함을 예상할 수 있다.

• 볼록 함수 $f(x)$

  모든 x와 y, 그리고 $0\leq \lambda \leq 1$에서 식 $f(\lambda x + (1-\lambda )y)\leq \lambda f(x)+(1-\lambda)f(y)$이 성립하는 함수

확산과 표준 편차 (Variance and standard deviation)

확률 변수의 기댓값만으로는 얼마나 값들이 확산되어있는지 알 수 없다.

확산(Variance)는 확률 변수의 값들이 평균에서 얼마나 동떨어져 있는 가에 대한 표현이다.

평균 기대값 E[X]에 대한 확률 변수 X의 확산은 다음과 같이 구할 수 있다.
\(\begin{align} Var[X] &= E[(X-E[X])^2]\\ &= E[X^2-2XE[X]+E^2[X]]\\ &= E[X^2]-2E[XE[X]]+E^2[X]\\ &= E[X^2]-2E^2[X] +E^2[X]\\ &= E[X^2]-E^2[X]\\ \end{align} \tag{3} \label{eq:variance}\)

위 식의 $E[E^2[X]]=E^2[X]$의 경우, 앞서 배운 기댓값의 선형성 2번 ()$E(aX+b)=aE(X)+b$)에 의해, $E[X]$의 값이 실수일 것이므로, $b$와 같은 상수로 취급 받아($E[X^2]=b$)

$E[E^2[X]]=E[b]=b=E^2[X]$가 되어 성립한다.

$E[XE[X]]=E^2[X]$은 기댓값의 선형성 2번과, 3번 ($E(XY)=E(X)E(Y)$)을 이용해 증명할 수 있다.

• $E[XE[X]]=E[X]E[E[X]]=E[X]E[X]=E^2[X]$

이렇게 증명한 확산의 식을 이용해 아래와 같이 확률 변수 제곱에 대한 기대값을 구할 수 있다.

$E[X^2]=Var[X]+E^2[X]$

확률 변수 X에 대한 확산과 aX에 대한 확산은 다음과 같은 관계를 가진다.

$Var[aX]=a^2Var[X]$

확률 변수 X와 Y가 상호 독립적이라면, 다음이 성립한다.

$Var[X+Y]=Var[X]+Var[Y]$

일반적적으로, n개의 확률 변수 $X_1,X_2,\dots,X_n$가 쌍방향 독립적이라면, 다음이 성립한다.
\(Var\left[\sum^n_{i=1}X_i\right]=\sum^n_{i=1}Var[X_i]\)

확률 변수 X의 표준 편차(standard deviation)는 확률 변수 X의 분산의 음이 아닌 제곱근이며, $\sigma_x$ 또는 $\sigma$로 표현한다. 즉, 확률변수 X의 분산은 $\sigma^2$이다.