알고리즘 수학 기본-확률

Jul 10, 2021

1. 확률(Probability)
   • 확률에 대한 공리(Axioms of probability)
   • 이산 확률 분포 (Discrete probability distributions)
   • 연속 균등 확률 분포 (Continuous uniform probability distribution)
   • 조건부 확률과 독립성(Conditional probability and independece)
   • 베이즈 정리(Bayes’s theorem)

알고리즘을 위한 수학 - 확률(Probability)

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.

이 장에서는 확률의 표기법, 정의, 속성 같은 기본적인 것만 배운다.

들어가기에 앞서 집합에 대한 기본적인 이해가 필요하므로 알고리즘을 위한 수학 -집합 편을 보고 오는 것을 추천한다.

---

확률(Probability)

확률은 확률적, 무작위성을 띄고 있는 알고리즘을 설계하고, 분석하는 중요한 장치이다.

우리는 확률을 확률적으로 더 이상 쪼개질 수 없는 최소 단위 사건인 근원 사건(elementary events)을 기본 원소로 하는 집합인 표본 공간(sample space) S에 대하여 정의한다.

예를 들어 2개의 동전 튕기기에서 각 튕김의 결과인 앞면, 뒷면을 각각 H, T 라고 정의할 때, 이를 근원 사건은 ${H, T}$이 존재하며, 표본 공간 S는 아래 같이 된다.

$S={HH, HT, TH, TT}$

사건(event)는 표본 공간 S에 대한 부분집합으로, 사건의 모음이라 할 수 있다. 예를 들어 앞면 하나, 뒷면 하나만 나올 사건은 ${HT, TH}$이다.

표본 공간과 같은 전체 근원 사건들의 집합 사건 S를 전사건(cetrain event)라고 하며, 사건 $\O$를 공사건(null event)이라 한다.

두 사건 A와 B가 만약 $A\cap B=\O$라면 상호배타적인 관계라고 하며, 모든 근원사건들은 서로에게 상호배타적이다.

가끔 표본 공간 S에 속한 근원사건 s를 사건 ${s}$로 생각하기도 한다.

확률에 대한 공리(Axioms of probability)

표본 공간 S에서의 확률 분포 $\Pr{}$는 S의 사건들을 실수로 투영한 것으로, 예를 들어 $\Pr{A}$는 사건 A가 일어날 확률이다. 또한, 다음 같은 확률 공리를 만족한다.

1. 모든 사건 A에 대해 $\Pr{A}\geq0$를 만족
2. $\Pr{S}=1$, 즉 모든 사건들의 합은 1, 이는 정규화(normalization)를 가능케 한다.
3. 모든 상호배타적 사건 A, B에 대하여 $\Pr{A\cup B}=\Pr{A}+\Pr{B}$를 성립,
   • 정확히는, 유한 또는 계수 가능 무한 이벤트 수열 $A_1,A_2,\dots$에 대해 모든 쌍은 아래와 같이 상호 배타적이다. (아래 이산 확률 분포 참고)
   • 즉, 각 사건이 일어날 확률들의 합은 모든 확률의 합이다.

\[\Pr\begin{Bmatrix} \bigcup_iA_i \end{Bmatrix}=\sum_i\Pr\{A_i\}\]

앞서 배웠던 집합에 대한 공리와 이론이 많은 연관을 가지고 있다.

먼저,

• $\Pr{\O}=0$, 즉 공사건의 확률은 0이다.

• 만약 $A\subseteq B$라면, $\Pr{A}\leq \Pr{B}$이며,

• 여사건 $\bar{A}$은 $S-A$로, 확률은 $\Pr{\bar{A}}=1-\Pr{A}$이 된다.

• 모든 경우의 두 사건 A, B에 대하여 다음이 성립한다.

\[\begin{align} \Pr\{A\cup B\}&=\Pr\{A\}+\Pr\{B\}-\Pr\{A\cap B\}\tag{1}\label{eq:equal} \\&\leq \Pr\{A\}+\Pr\{B\}\tag{2}\label{eq:bound} \end{align}\]

이산 확률 분포 (Discrete probability distributions)

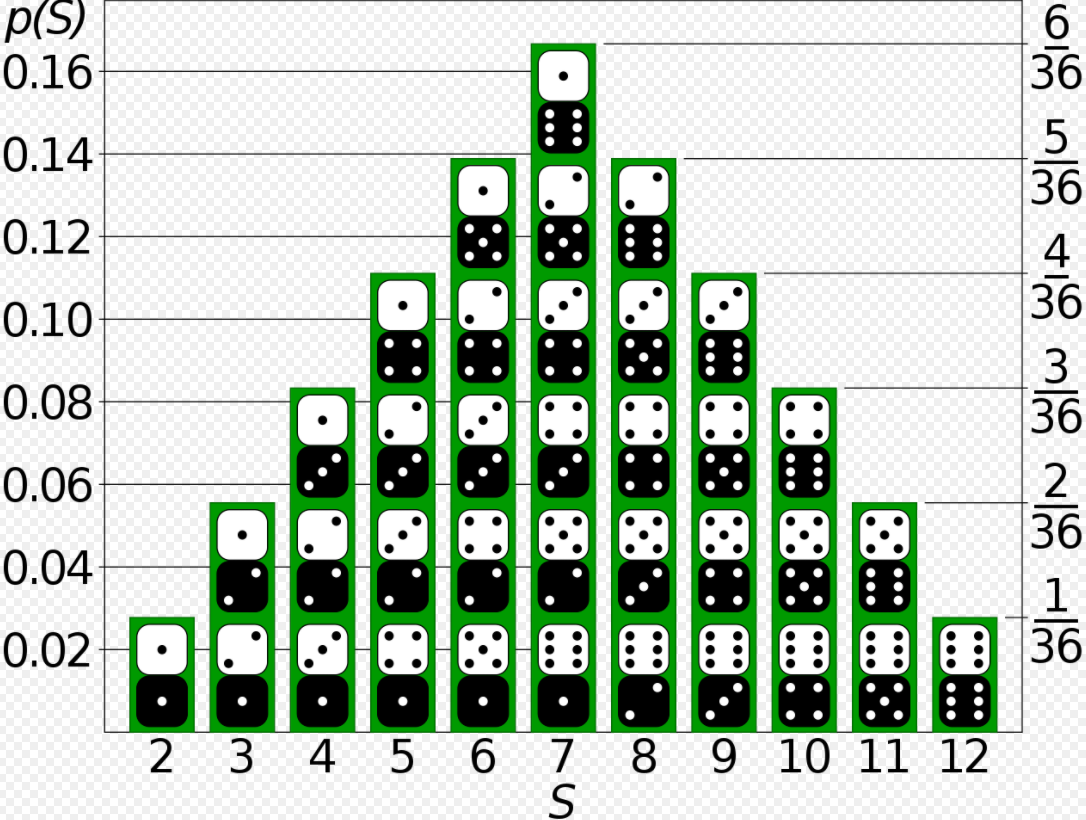
• 주사위 던지기에 대한 이산 확률 분포, 각 사건의 확률들이 동일한 값을 가진 다른 사건이 존재하거나 다른 확률의 배수인 것 등을 확인할 수 있는데, 이산 확률 분포는 확률 변수가 가질 수 있는 값의 갯수가 가산개라는 특징이 있다.

만약 유한하거나 계수 가능 무한한 표본 공간 S에 대해서 확률 분포가 정의된다면, 이를 이산 확률 분포 (Discrete probability distributions)라고 한다.

상호배타적인 근원사건으로 구성된 사건 A에 대해 다음이 성립한다.

$\Pr{A}=\sum_{s\in A}\Pr{s}$

만약 표본 공간 S가 유한하다면, S에 속한 모든 근원사건 s의 확률은 다음과 같이 된다.

$\Pr{s}=1/

S

$

이는 균등 확률 분포(uniform probability distribution)를 나타나게 한다.

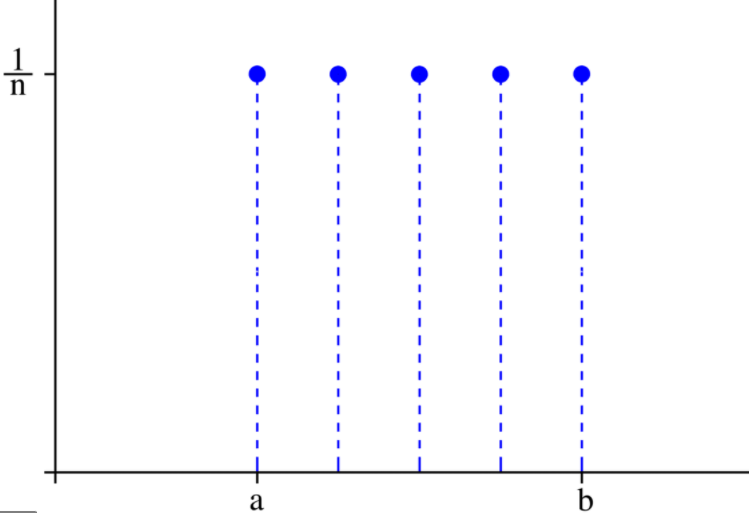
• 균등 분포의 예, 두 사건 a, b의 확률이 같음을 알 수 있다.

예를 들어 앞뒤가 나올 확률이 1/2로 동일한 동전이 있을 때, 코인을 n번 튕기면, 표본 공간 $S ={H,T}^n,

S

=2^n $에 대한 균등 확률 분포를 얻을 수 있다.

우리는 S의 근원 사건을 H와 T로 이루어진 길이 n의 문자열로 나타낼 수 있으며, 각 문자열의 확률은 $(1/2)^n$이다.

• 예를 들어, 동전을 3번 던진다면, HHH, HHT, HTH, THH, HTT, THT, TTH, TTT 총 8개의 문자열이 나올 것이며, 각 확률은 1/8이다.

사건 A는 정확히 k번의 앞면과 n-k번의 뒷면이 나올 방법이며, 크기가 $

A

=\binom{n}{k}$인 S의 부분집합이다.

사건 A의 확률은 $\Pr{A}=\binom{n}{k}/2^n$이다.

• 예를 들어 3번 동전을 던져 2번의 앞면과 3-2번의 뒷면이 나올 사건 A가 포함하는 근원 사건은 HHT, HTH, THH이며, 사건 A의 크기는 $

  A

  =\binom{3}{2}=\frac{3!}{2!1!}=3$이며, 사건 A의 확률은 $\Pr{A}=\binom{3}{2}/2^3=3/8$이다.

연속 균등 확률 분포 (Continuous uniform probability distribution)

연속 균등 확률 분포 (Continuous uniform probability distribution)는 표본 공간의 일부 부분집합이 사건으로 여겨지지 않는 확률 분포의 예이다.

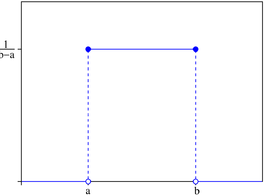
연속 균등 확률 분포는 a< b인 닫힌 실수 구간 [a,b] 사이로 정의되며, [a, b] 사이의 실수 점들이 무수히 많기 때문에 모든 점들이 같은 확률을 가진다면, 확률의 총합이 1이 넘어가버린다. 따라서, S의 일부 부분집합에만 확률을 적용한다.

• 보통 특정 구간 [a, b]나 (a, b)의 유한 또는 가산 가능한 부분집합이나, 좀 더 복잡한 집합들을 포함한다.

일정 구간 [c,d]에 대해, $a\leq c \leq d \leq b$를 만족할 때, 사건 [c, d]의 확률은 $\Pr{[c,d]}=\frac{d-c}{b-a}$로 정의 된다.

만약, 구간이 [x, x]처럼 시작과 끝이 동일한 경우에 확률은 0이 된다.

닫힌 구간 [c,d]의 양 끝단 지점, [c, c]와 [d, d]를 지운 구간을 열린 구간 (c, d)라고 표기한다고 하면, $[c,d]=[c,c]\cup(c,d)\cup[d,d]$를 만족하며, 양 끝단의 확률은 0이므로, $\Pr{[c,d]}=\Pr{(c,d)}$를 만족한다.

조건부 확률과 독립성(Conditional probability and independece)

조건부 확률은 부분적인 사전 지식이 있을 때의 확률을 의미하며, 예를 들자면, 동전 1개 이상의 앞면이 확정되었을 때, 동전 2개가 전부 앞면일 확률이다.

원래는 둘다 앞면일 확률은 1/4이겠지만, 동전 1개 이상이 앞면으로 확정되었으므로, 뒷면이 2개가 나올 확률이 없어져, 1/3으로 바뀐다.

사건 B가 확정된 상황에서 A가 일어날 조건부 확률($\Pr{A|B}$)은 아래와 같이 정의 된다.
\(\Pr\{A|B\}=\frac{\Pr\{A \cap B\}}{\Pr\{B\}} \tag{3} \label{eq:conditional probability}, where\ \Pr\{B\}\neq 0\)

이때, $A \cap B$는 사건 A와 사건 B가 같이 일어난 결과(outcome)(=둘 다 만족하는 결과)의 집합이며, 이때 결과(outcome)은 표본 공간의 원소를 의미한다.

$A\cap B$에 속한 결과들은 사건 B의 근원 사건이기도 하므로, $\Pr{B}$로 나누어 정규화되며, 따라서 사건 B의 근원사건의 확률을 모두 더하면 1이 나온다.

따라서 B가 확정된 A의 조건부 확률은 사건 $A \cap B$의 확률과 사건 B의 확률 간의 비율이며, 예를 들면 사건 A는 두 동전이 모두 앞면이 나올 확률이며, B는 적어도 하나의 동전이 앞면일 확률이다. $\Pr{A

B}=(1/4)/(3/4)=1/3$이 나옴을 알 수 있다.

만약 두 사건이 $\Pr{A\cap B}=\Pr{A}\Pr{B} \tag{4} \label{eq:independent condition}$가 성립된다면, 두 사건은 독립적(independent)이라고 한다.

• 예를 들어 서로 다른 두 동전의 앞면이 나올 확률은 각각 1/2, 1/2이며, 두 동전다 앞면이 나올 확률은 (1/2)(1/2) =1/4이므로, 위 식을 만족하여 이 두 사건은 서로 독립적이다.

위의 식 $\eqref{eq:independent condition}$은 $\Pr{B}\neq 0$일 때, $\Pr{A

B}=\Pr{A}$과 동치이다.

만약 1개 이상의 사건들 $A_1,A_2,\dots,A_n$의 집합이 쌍방향 독립적(pairwise independent)이라면, $1\leq i<j\leq n$에 대해 $\Pr{A_i\cap A_j}=\Pr{A_i}\Pr{A_j}$을 만족한다.

만약 1개 이상의 사건들 $A_1,A_2,\dots,A_n$의 집합이 상호 독립적(mutually independent)이라면, $1\leq i_n<i_{n+1}\leq n$에 대해 $\Pr{A_{i_1}\cap A_{i_2}\cap\cdots\cap A_{i_k} }=\Pr{A_{i_1}}\Pr{A_{i_2}}\cdots\Pr{A_{i_k}}$을 만족한다.

만약 $A_1$을 첫번째 동전이 앞면이 나오는 사건, $A_2$를 두번째 동전이 앞면이 나오는 사건, $A_3$를 두 동전이 서로 다른 면이 나오는 사건이라고 하면, 확률은 다음과 같다.
\({align} \Pr\{A_1\}=1/2,\\ \Pr\{A_2\}=1/2,\\ \Pr\{A_3\}=1/2,\\ \Pr\{A_1 \cap A_2\}=1/4,\\ \Pr\{A_1 \cap A_3\}=1/4,\\ \Pr\{A_2\cap A_3\}=1/4,\\ \Pr\{A_1\cap A_2\cap A_3 \}=0\) {algin}

$1\leq i < j \leq 3$에서 $\Pr{A_i \cap A_j}=\Pr{A_i}\Pr{A_j}=1/4$를 만족하므로, 쌍방향 독립적이지만,

$\Pr{A_1\cap A_2\cap A_3}=0$이며, $\Pr{A_1}\Pr{A_2}\Pr{A_3}=1/8\neq0$이므로 상호 독립적이지 않다.

베이즈 정리(Bayes’s theorem)

조건부 확률의 정의 $\eqref{eq:conditional probability}$와 교환 법칙 $A\cap B =B\cap A$에 의해 두 사건 A와 B가 확률이 0이 아닌 사건일 때, 다음과 같은 식이 성립한다.
\(\Pr\{A \cap B\}&= \Pr\{B\}\Pr\{A|B\}\\\label{eq:eq by commutative law}\tag{5}&=\Pr\{A\}\Pr\{B|A\}\)

이를 통해 다음과 같은 식, 베이즈 정리(Bayes’s theorem)를 얻을 수 있다.
\(\Pr\{A|B\}=\frac{\Pr\{A\}\Pr\{B|A\}}{\Pr\{B\}} \label{eq:Bayes's theorem} \tag{6}\)

분모 $\Pr{B}$는 정규화 상수(normalizing constant)로, 다음과 같은 식으로 변경할 수 있다.

$B=(B\cap A)\cup(B\cap\bar{A})$이고, $B \cap A$와 $B \cap \bar{A}$가 상호배타적 사건일 때, 다음이 성립한다.
\(\begin{align} \Pr\{B\}&=\Pr\{B\cap A\}+\Pr\{B\cap \bar{A}\}\\ &=\Pr\{A\}\Pr\{B|A\}+\Pr\{\bar{A}\}\Pr\{B|\bar{A}\} \end{align}\)

이 값을 식 $\eqref{eq:Bayes’s theorem}$의 분모와 바꾸면, 다음과 같은 베이즈 정리의 동치 형태 식이 나온다.
\(\Pr\{A|B\}=\frac{\Pr\{A\}\Pr\{B|A\}}{\Pr\{A\}\Pr\{B|A\}+\Pr\{\bar{A}\}\Pr\{B|\bar{A}\}} \tag{7}\label{eq: equivalent form of Bayes's theorem}\)

베이즈의 정리는 조건부 확률을 구하는데 편리하다.

예를 들어, 무조건 앞면만 나오게 되는 편향된(biased) 동전과 확률이 동일한 공평한 동전이 존재한다고 하자.

이 두 동전 중 하나를 무작위로 골랐고, 해당 동전을 2번 튕겼을 때 두번 다 앞면이 나왔다고 가정하자, 이때 이 동전이 편향된 동전이였을 확률은 얼마나 되는가?

이를 베이즈 정리를 이용해 풀 수 있는데, 사건 A를 편향된 동전을 골랐을 확률, 사건 B를 두 번의 기회 전부 앞면이 나올 확률이라고 할 때, $\Pr{A

B}$를 구해보자.

$\Pr{A}=1/2$, $\Pr{B|A}=1$, $\Pr{\bar{A}}=1/2$, $\Pr{B|\bar{A}}=1/4$(공평한 동전의 경우 1/4 확률로 두번 다 앞면이 나올 확률)이며, 다음과 같이 구하게 된다.
\(\Pr\{A|B\}=\frac{(1/2)\cdot 1}{(1/2)\cdot 1+ (1/2)\cdot(1/4)}=4/5\)