알고리즘 수학 기본-함수

Jul 6, 2021

1. 함수(functions)
2. 전사함수(Surjection), 단사함수(Injection) 그리고 전단사함수(Bijection)

알고리즘을 위한 수학 - 함수(functions)

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.

이 장에서는 함수의 표기법, 정의, 속성 같은 기본적인 것만 배운다.

앞선 알고리즘을 위한 수학 - 집합(Sets)편을 먼저 보고 오는 것을 추천한다.

함수(functions)

함수 $f$는 두 집합 A, B의 원소 a, b에 대하여, a에 대한 b의 값이 정확히 하나씩만 대응되는 이항관계이다.

이때 집합 A를 함수 $f$의 정의역(domain, 도메인), 집합 B를 함수 $f$의 공역(codomain, 부도메인)이라 하며, $f:A\rightarrow B$로 표현한다.

이때 정의역의 원소 a와 공역의 원소 b의 관계가 성립된다면$(a,b)\in f$, $b=f(a)$로 표기하며, 이때 b의 값은 오직 원소 a의 값에 의해서만 결정된다.

• $b=f(a)$에서 정의역의 원소 a는 함수 f의 인자(argument)이며, 정의역이 원소 b는 함수 f의 값(value)이다.

  만약, 정의역이 곱집합으로 되어있는 경우에는 괄호를 활용해 인자를 표현한다. 예를 들어 $f:A_1\times A_2 \times \cdots \times A_n \rightarrow B$는 $f(a_1,a_2,\cdots,a_n)$으로 표현된다.

  사실, 엄밀히 말하면 $(a_1,a_2,\cdots,a_n)$ 형태의 n-튜플이 통째로 하나의 인자이며, $f((a_1,a_2,\cdots,a_3))$가 옳은 표현이지만, 각 $a_i$를 하나의 인자로 보고, 여러개의 인자가 들어가 있는 것으로 표현한다.

앞서 언급했듯이,인자 a는 오직 한 값 b에 대응되지만, b은 여러 인자 a값에 대응될 수 있다.

예시로, 함수 $f={(a,b):a,b\in \N\ and\ b=a\mod2}$의 경우, $f:\N \rightarrow {0,1}$로 표현하며, a 값은 b값으로 0 또는 1만 가질 수 있고, b는 많은 수의 a를 가진다.

반대로 이항관계 $g={(a,b):a,b\in \N\ and\ a+b는\ 짝수}$에서는 예를 들어 a가 홀수이면, 나머지 모든 홀수들이 전부 b가 될 수 있으며, 함수의 정의 중, 정의역의 원소가 여러 공역의 원소에 대응되서는 안되므로, 함수가 될 수 없다.

그러므로 함수는 각 값에 대해 하나의 인자, 즉, 하나의 정의역의 원소를 대응시켜 주어 정의할 수 있으며, 만약 두 함수 $f$와 $g$의 정의역과 공역이 같다면, 두 함수는 같은 걸로 정의한다.

전사함수(Surjection), 단사함수(Injection) 그리고 전단사함수(Bijection)

수학에서 상(image)은 어떤 함수에 대한 정의역의 원소들에 대응하는 공역의 원소들이며, $b=f(a)$에서 b를 의미한다. 이를 이용해 부분집합 $A’$를 다음과 같이 표현할 수 있다.

$f(A’)={b\in B:b=f(a)\ for\ some\ a \in A’}$

또한, 함수의 치역(range)은 정의역의 상(image), 즉 함수의 출력값들의 집합을 의미하며, 정의역 집합 A에 대해 $f(A)$로 표현된다.

예를 들면 $f(n)=2n$에서 치역은 $f(\N)={m:m=2n\ for\ some\ n \in \N}$, 즉, 양수의 짝수 정수로 이루어진다.

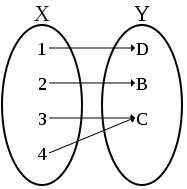
전사함수(surjection, surjective funtion) 또는 A 위로의 B 함수( A onto B)은 이러한 치역(range)와 공역(codomain)이 같은 함수를 의미한다.

즉, 공역의 모든 원소들이 어떤 정의역 원소들에 의해 하나도 빠짐없이 대응되고 있어야 한다. 이때, 정의역 원소의 중복을 허용한다.

함수 $f(n)=\left \lfloor n/2 \right \rfloor$의 경우, n의 값이 바뀌면서 모든 정수를 $\N$의 모든 값이 함수의 결과값으로 나오므로 전사함수이다.

하지만, 함수 $f(n)=2n$의 경우, 함수의 결과값은 언제나 짝수로 나오므로, 홀수 정수는 대응되는 정의역 원소가 없으므로 전사함수가 아니다.

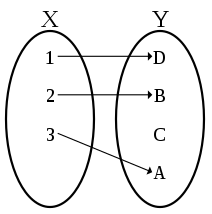
단사함수(injection, injective function), 또는 일대일(one-to-one) 함수는 각기 다른 정의역의 원소가 각기 다른 공역의 원소에 대응 되는 함수를 의미한다.

즉, $a\neq a’$은 곧 $f(a)\neq f’(a)$를 의미한다.

전사함수의 예시와 반대로 함수 $f(n)=\left \lfloor n/2 \right \rfloor$의 경우, n의 값이 바뀌어도 같은 결과값이 나올 수 있으므로, 단사함수가 아니다.(n이 2,3 이 전부 같은 1이 나온다.)

하지만, 함수 $f(n)=2n$의 경우, 함수의 결과값은 n의 2배인 짝수가 나오므로, 중복되는 결과값이 없어 단사 함수이다.

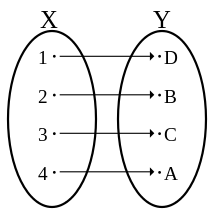
전단사함수(bijection, bijective function) 또는 일대일 대응(one-to-one correspondence) 함수(일대일 함수와 다르다)는 전사함수와 단사함수가 합쳐진 것으로, 즉 정의역과 공역의 원소들이 하나도 빠짐없고 중복없이 모두 일대일 대응되는 함수이다.

예를 들어 함수 $f(n)=(-1)^n \left \lceil n/2 \right \rceil$의 경우 정의역 $(0, 1, 2, 3, 4)$에 대해 순서대로 $(0,-1,1,-2,2)$가 생성되므로 전단사함수이다.

집합 A가 정의역이자 공역이 같은 전단사 함수, 즉 자기자신과 일대일 대응되는 전단사함수는 순열(permutation)이라고도 부른다.

• 집합 A의 원소가 함수에 대입되 집합 A의 다른 원소가 나오는 꼴이 마치 자리가 바뀌는 것 처럼 보이므로. 물론, 자리가 바뀌지 않고 같은 값이 나와도 전단사 함수이며, 순열의 경우의 수중 하나이다.

또한 전단사 함수의 성질로, 정의역과 공역이 반전되어 있는 형태의 역함수 $f^{-1}(b)=a$로 표현될 수 있으며, 위에서 언급한 함수$ f(n)=(-1)^n \left \lceil n/2 \right \rceil$ 의 역함수를 예시로 들자면
\(f^{-1}(m)=\left\{\begin{matrix} 2m\ & if \ m\geq0 \\ -2m-1 & if\ m < 0 \end{matrix}\right.\)