알고리즘 수학 기본-트리

Jul 11, 2021

1. 자유 트리(Free trees)
2. 트리에 관한 정리 : 자유 트리의 성질 (Thorem for tree: Properties of free trees)
   • 자유 트리의 성질
   • 증명
3. 루트 존재 트리와 순서 트리(Rooted and ordered trees)
4. 이진 트리와 위치 트리(Binary and positional trees)

알고리즘을 위한 수학 - 트리(trees)

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.

이 장에서는 트리의 표기법, 정의, 속성 같은 기본적인 것만 배운다.

앞선 알고리즘을 위한 수학 - 그래프(graphs)편을 먼저 보고 오는 것을 추천한다.

---

자유 트리(Free trees)

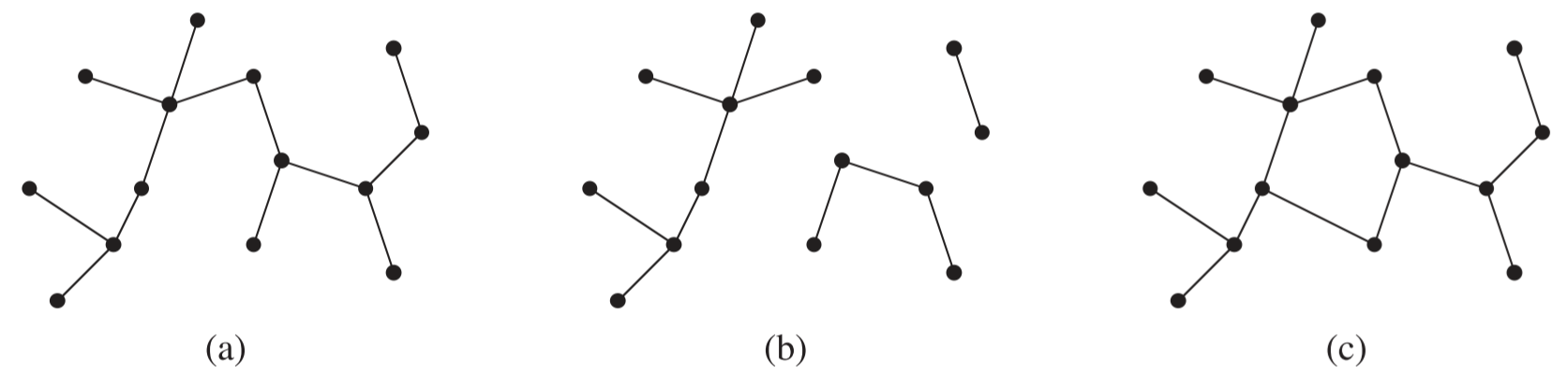
앞서 그래프편에서 정의했듯이 자유 트리는 acyclic 무향 연결 그래프이다. 아래 Figure 1 (a)는 자유 트리를 나타낸다.

만약, 그래프가 acyclic 무향 비연결 그래프라면, 포레스트 그래프라고 부른다. 아래 Figure 1 (b)는 포레스트를 나타낸다.

사이클이 존재하는 Figure 1 (c)는 사이클이 존재하므로 트리도, 포레스트도 아니다.

트리에 적용할 수 있는 알고리즘들은 대부분 포레스트에도 적용할 수 있다.

트리에 관한 정리 : 자유 트리의 성질 (Thorem for tree: Properties of free trees)

자유 트리의 성질

무향 그래프 $G=(V,E)$에 대하여 다음과 같은 문장들은 모두 동일한 의미다.

1. G는 자유 트리이다.
2. G의 모든 한쌍의 정점은 유일한 단순 경로(simple path)로 연결되어 있다.
3. G는 연결 그래프이며, 만약 어느 간선이라도 하나 없어지면, G는 비연결 그래프가 된다.

4. G는 연결 그래프이며, $

   E

   =

   V

   -1$이다.

5. G는 acyclic이며, $

   E

   =

   V

   -1$이다.

6. G는 acyclic이며, 간선이 어느 곳이든 하나 추가되면, 사이클이 존재하는 그래프가 된다.

증명

위의 n번째 문장일 때 n+1 문장이 성립하고 마지막 문장에 의해 첫번째 문장이 성립한다는 것을 증명하면 모두 동일하다는 것이 증명된다.

그래프 G가 자유트리이면 모든 정점쌍은 유일한 단순 경로로 연결된다.

G는 1번에서 자유 트리로 가정했으므로, 어느 두 정점 간의 경로는 최소 하나의 간단 경로로 이어져 있다.

아래의 Figure 2처럼 만약 두 임의의 정점 u와 v가 서로 다른 단순 경로 $p_1$과 $p_2$로 연결되어 있다고 가정하자

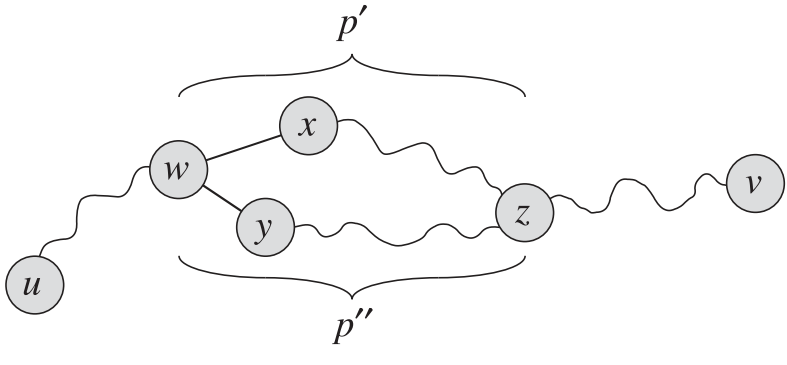
w는 u에서 v로 향할 때, 두 경로 $p_1,p_2$가 각각 정점 x와 정점 y로 갈라지는 갈림길 정점이다. 또한 정점 z는 이 갈라진 두 경로가 v로 도착하기 위해 통합되는 정점이다.

이때 $p’$는 정점 w와 정점 z 간의 $p_1$의 부분 경로이고, $p’‘$는 정점 w와 정점 z간의 $p_2$의 부분 경로이다. 이 두 부분경로 $p’,p’‘$는 시작 정점 w와 끝 정점 z를 제외하고 경로상에 다른 정점을 공유하지 않는다.

따라서 $p’$와 $p’‘$를 뒤집은 경로, 또는 $p’‘$와 $p’$를 뒤집은 경로에 의해 정점 w와 정점 z를 포함한 사이클이 생성되며, 이는 G가 자유 트리라는 가정에 모순된다.

따라서 자유 트리이면, 모든 정점쌍 간에는 단 하나의 유일한 단순경로를 가지게 된다.

그래프 G 내의 모든 정점쌍이 유일한 단순 경로로 연결된다면, G는 연결 그래프이며, 간선이 하나라도 없어지면 비연결 그래프가 된다.

어떤 정점쌍 u, v가 간선 (u,v) 하나로 이어진다면, 해당 간선은 정점쌍 u, v에 대한 유일한 단순경로일 것이다.

만약 이 간선이 지워진다면, u와 v 사이를 연결해주는 경로가 없어진다.

해당 경로는 유일하였으므로, 이제 더 이상 u와 v를 통하는 경로가 없어지게 된다. 따라서 G는 비연결 그래프가 된다.

G는 연결 그래프이며, 간선이 하나라도 없어지면 비연결 그래프가 된다면, $|E|=|V|-1$이다.

연결 그래프 G 에 대하여 $|E|\geq |V|-1$ 증명

먼저 연결 그래프 G가 $

E

\geq

V

-1$임을 수학적 귀납 방법으로 증명해보자면,

최초, 정점이 1개 일때(=$

V

=1$)일때는 간선이 필요 없으므로(=$

E

=0=

V

-1$) 증명된다.

이제 정점이 n개일 때의 간선의 수를 구해보자, 정점의 갯수 n-1일 때의 그래프 $G’$는 연결 그래프로, 정점이 $

V’

=n-1$이고 간선의 수는 $

E’

\geq

V’

-1 = n-2$일 것이다.

이 그래프 $G’$에 새로운 정점 w를 추가로 붙이면 연결 그래프인 G가 생성될 것이며, $

V

=n-1+1=n$이다.

연결 그래프여야 하므로, 정점 w는 고립 정점이면 안되므로, 간선 1개 이상을 추가해서 그래프 $G’$에 정점 w를 이어야 한다.

새로 연결한 간선의 수를 $k(k\geq 1)$라고 하면 새로운 그래프 $G$의 간선의 수는 $

E

\geq

E’

+k\geq n-2+k \geq n - 1$이다.

따라서 $

V

=n,

E

\geq

V

-1$이된다.

---

연결 그래프 G에 대하여 $|E| \leq |V|-1$ 증명

이제 우리는 연결 그래프 G에 대하여 $

E

\leq

V

-1$ 를 증명하면 앞서 증명한 $

E

\geq

V

-1 $과 결합해 $

E

=

V

-1$을 증명할 수 있다.

먼저 정점이 1개 또는 2개일 때는 $

E

\leq

V

-1$이 성립하며, 3개 이상 부터는 다음과 같이 증명한다.

먼저 $

E

\leq

V

-1$을 만족하는 연결 그래프 G에서 간선 하나를 제거하여 $k\geq 2$개의 연결요소(conneceted components) $G_i=(V_i,E_i)$로 나눈다.

각 연결요소들은 마찬가지로 연결 그래프이면서, 자유트리이다. 원본 그래프 G가 연결 그래프였기 때문이다.

이때 각 연결요소의 정점 갯수 $V_i$은 원본 그래프 G의 정점 갯수 V보다 작으므로 정점 갯수 1,2일 때도 성립하고 G도 성립한다는 점을 이용한 귀납적 가정을 통해 $

E_i

\leq

V_i

-1$가 성립한다.

따라서 전체 연결요소들의 간선의 수는 $\sum^i_{n=0}E_i=

V

-k\leq

V

-2$이다.

나눌 때 제거했던 간선 1개를 추가해준다면 $

E

\leq

V

-1$가 된다.

---

G는 연결 그래프이며, $|E|=|V|-1$이면, G는 Acyclic이다.

G에 k개의 정점 $v_1,v_2,\cdots, v_k$를 포함한 단순 사이클이 존재한다고 가정하고, G의 부분 그래프 $G_k=(V_k,E_k),

V_k

=

E_k

=k$가 이 사이클만으로 이뤄졌다고 하자.

k가

V

보다 작다면, G는 연결 그래프이므로 사이클에 포함된 정점 중 하나와 연결된 사이클에 속하지 않은 정점 $v_{k+1}$이 존재할 것이다.

$v_{k+1}$을 포함한 새로운 부분 그래프 $G_{k+1}=(V_{k+1},E_{k+1})$라고 하고, 이때도 마찬가지로 $

V_{k+1}

=

E_{k+1}

=k+1$ 를 만족한다.

만약 k+1 또한

V

보다 작다면, $G_{k+1}$에 속하지 않으면서, $G_{k+1}$과 연결된 새로운 정점 $v_{k+2}$를 이용해 $G_{k+2}$를 만들어 볼 수 있으며, 이를 $n =

V

$까지 적용해 $

E_n

=

V_n

=

V

$까지 증명할 수 있다.

이 $G_n$은 G의 부분 그래프로, $E_n$은 0개이상의 간선이 E에서 빠진 것으로, $

E_n

=

V

,

E_n

\leq

E

$이므로 $

E

\geq

V

$인데, 이는 $

E

=

V

-1$을 위반하므로 처음의 가정, “단순 사이클이 존재한다”는 모순된 이야기가 되므로, G는 단순 사이클이 없는 acyclic 이다.

G는 Acyclic이며, $|E|=|V|-1$이면, 간선이 하나라도 추가되면 사이클이 생겨난다.

k를 G의 연결 요소 갯수로 놓고, 각 연결 요소는 정의에 의해 자유 트리이다.

G 또한, 앞서서 1번째 문장이 5번째 문장까지 일치한다는 것을 증명했으므로, G는 자유트리이며, 모든 연결요소들의 간선의 합은 $

V

-k$이다.

G 는 트리이므로, k=1이 되며, 2번째 문장에 의해 이미 G에는 모든 정점쌍의 유일한 단순 경로가 존재하므로, 간선을 추가하면 사이클이 생긴다.

G는 간선이 하나라도 추가되면 사이클이 생겨나는 Acyclic 그래프이면, G는 자유 트리이다.

여기선 G가 연결 그래프란 점만 보이면 되는데, G 내의 모든 정점 중의 어떤 정점 둘 u, v를 가정하자.

u와 v는 직접 이웃하지 않는다면, 간선 (u,v)를 추가하면 그래프 내에 사이클이 생겨난다.

사이클이 생긴다는 것은, 이미 u와 v를 연결하는 경로가 존재한다는 의미이며, u와 v는 모든 정점 중에서 둘을 고른 것이므로, 모든 u와 v에는 경로가 존재한다는 의미이며, 이는 G가 연결 그래프란 의미이다.

G가 연결 그래프이고 Acyclic인 무향 그래프이므로 G는 자유트리이다.

루트 존재 트리와 순서 트리(Rooted and ordered trees)

루트 존재 트리는 루트(뿌리, root)라고 불리우는 정점이 하나 존재하는 자유트리이다.

루트 존재 트리에서의 정점은 노드(node)라고도 부르며, Figure 3은 7번 노드를 루트로 하는 12개의 노드를 포함한 루트 존재 트리이다.

루트 노드가 r인 루트 존재 트리 T의 노드 x가 존재할 때, x와 r 간의 경로 사이에 존재하는 어떤 노드 y를 노드 x의 조상(ancestor)라고 하며, 반대로 노드 x는 노드 y의 후손(descendant)이라고 한다. 또한 모든 노드는 자기 자신의 조상이면서 후손이다.

이때 자기자신을 제외한 조상과 후손 노드들을 각각 정조상(proper ancestor), 정후손(proper descendant) 노드라고 하며, 루트를 x로 하는 부분 트리는 노드 x의 후손을 가지고 있다.

만약 루트 r로부터 노드 x까지로 가는 경로의 마지막에 위치한 간선을 (y,x)라고 할 때, 노드 y는 x의 부모(parent)이고, 노드 x는 y의 자식(child)이다.

루트 노드 r은 트리 내에서 유일하게 부모가 없는 노드이며, 같은 부모를 공유하는 노드들은 형제(siblings) 노드이다.

자손이 없는 노드를 리프(leaf) 노드 또는 외부(external) 노드 라고 하며, 리프 노드가 아닌 노드를 내부(internal) 노드라고 한다.

루트 존재 트리의 노드 x의 자식의 수를 x의 차수(degree)라고 한다. 이는 그래프에서 인접한 모든 노드를 차수로 놓는 것과 달리 부모를 제외하고 차수로 친다.

루트 r 부터 노드 x까지의 경로의 길이를 T에서의 x 노드의 깊이(depth)라고 하며, 같은 깊이의 노드들의 집합을 레벨(level)이라고 한다.

트리의 높이(height)는 리프 노드로 향하는 자식 방향(아래 방향)의 가장 긴 경로의 간선의 수이며, 트리의 높이는 곧 루트의 높이다. 또한 트리의 높이는 가장 깊이 값이 큰 노드의 깊이 값과 같다.

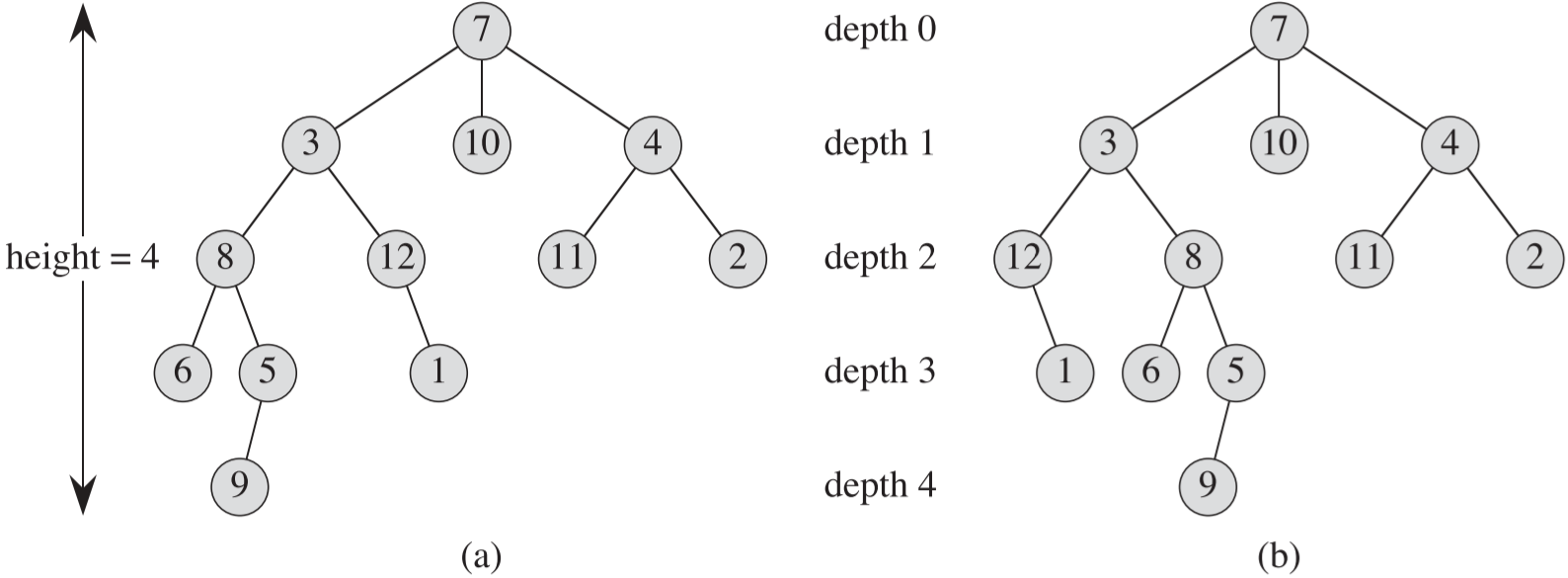
순서 트리(ordered tree)는 각 노드의 자식들이 정렬되어 있는 루트 존재 트리이다.

즉, 노드에 k 개의 자식이 있다면, 오름차순 혹은 내림차순으로 자식들이 배치된다. Figure 3 (a)와 (b)는 루트 존재 트리로써 동일하지만, 순서 트리로써는 서로 다른 트리이다.

이진 트리와 위치 트리(Binary and positional trees)

이진 트리(Binary tree)는 재귀적으로 정의되는데, 노드들은 다음 두 종류를 포함한다.

• 아무 노드도 포함하지 않거나
• 세가지 노드들의 서로소 집합, 루트 노드, 좌측 부분 이진트리, 우측 부분 이진트리

아무 노드도 포함하지 않은 이진 트리를 빈 트리(empty tree) 또는 널 트리(null tree) 또는 NIL 이라고 부른다.

만약 왼쪽 부분 트리가 비어있지않으면, 왼쪽 부분 트리의 루트 노드를 루트의 좌측 자식이라고 하며, 오른쪽일 경우 루트의 우측 자식이라고 한다.

만약 부분 트리가 NIL 이라면, 자식이 없거나 비어있다고 표현한다. 아래 그림 Figure 4의 (a)가 이진 트리이다.

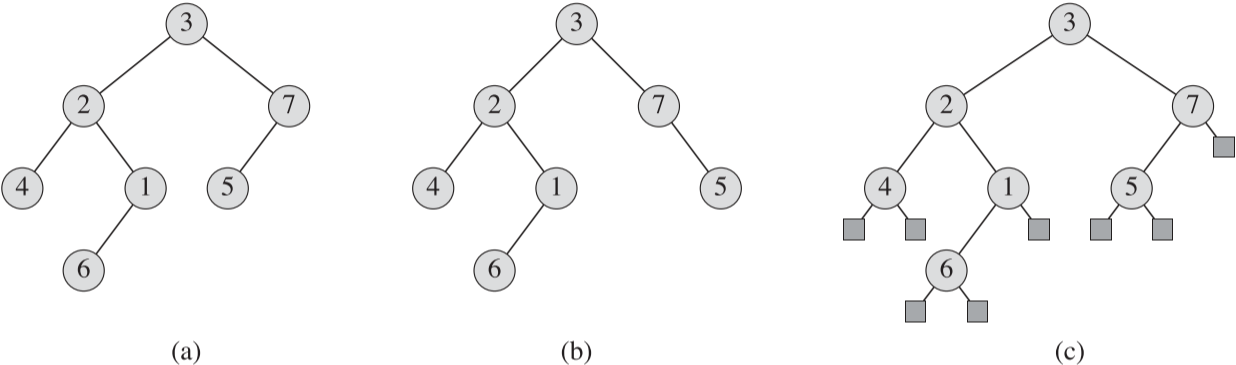
다만, 순서 트리에서는 자식이 하나만 있다면, 자식의 위치, 즉 왼쪽 자식이든 오른쪽 자식이든 구분하지 않는다.

• 위에서 설명했던 Figure 3의 두 트리와 비교하자, 만약 순서 트리의 노드의 차수가 2라면, 그때는 왼쪽 자식 오른쪽 자식을 엄격하게 구분한다!

Figure 4의 (a)와 (b)는 7번 노드의 자식, 5번 노드가 좌측, 우측 노드 차이로 인해 다른 이진 트리로 분류되지만, 만약 순서 트리라면 (a)와 (b)는 같은 트리로 분류된다.

이진 트리 내의 위치 정보를 순서 트리의 내부 노드를 이용하여 나타낼 수 있다.

1. 순서 트리의 자식이 비어있는 노드들의 빈 노드 자리에 Figure 4의 (c)처럼 사각형으로 표기된 특별 리프 노드를 집어 넣어 전 이진 트리(full binary tree)로 만든다.
   • 즉, 모든 노드들이 리프 노드이거나 차수가 2가 되게 만든다.
2. 이제 루트 노드를 제외한 모든 자식 노드들에 순서가 부여되어 위치 정보를 나타낸다.
   • 순서 트리는 원래 자식이 하나일 때는 위치가 구분되지 않았지만, 이제 모두 자식이 둘이므로 자식의 위치가 중요하게 되므로 특별한 정보를 가지게 된다.

이러한 방법으로 순서 트리의 노드들에게 구분되는 양수를 주어 순서트리와 다른 위치 트리(positional tree)를 만들 수 있는데, 이때 이진트리 뿐만 아니라 노드가 최대 k개의 자식을 가질 수 있는 k진 트리를 이용할 수 있다.

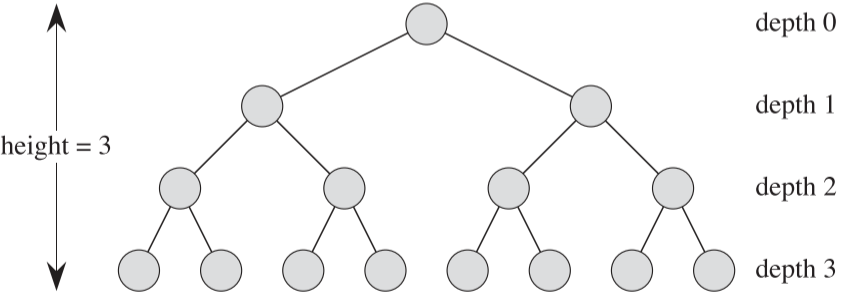
완전 k진 트리(complete k-ary tree)는 모든 리프 노드가 동일한 레벨을 가지고, 모든 내부 노드의 차수가 k인 트리이다. 아래 Figure 5는 높이가 3인 완전 이진 트리를 보여준다.

이때, 완전 k진 트리의 특정 높이 h를 가지는 노드의 갯수는 $k^h$로 구할 수 있다. 예를 들어, 깊이가 0일 때는 루트 노드 1개, 깊이가 1일 때는 2개이다.

따라서 완전 k진 트리의 리프 노드의 갯수는 총 $k^h$개 이며, 결과적으로 완전 k진 트리의 높이는 리프 노드의 갯수가 n이라 할때 $\log_kn$이다.

완전 k진 트리의 내부 노드의 숫자는 다음과 같이 구할 수 있다.
\(1+k+k^2+\cdots +k^{h-1}=\sum^{h-1}_{i=0}k^i=\frac{k^h-1}{k-1}\)
따라서 완전 이진 트리의 모든 노드의 갯수는 $2^h -1$이다.