알고리즘 수학 기본-집합

Jul 10, 2021

1. 집합 (Sets)
   • 집합의 기본 표현과 원소와의 관계 표현
   • 집합 간의 관계 표현
   • 집합 연산
   • 서로소 집합(disjoint set)
   • 카디널리티(cardinality)
   • 순서쌍(ordered pair)
   • 곱집합(Cartesian product)

알고리즘을 위한 수학 - 집합(Sets)

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.

이 장에서는 집합의 표기법, 정의, 속성 같은 기본적인 것만 배운다.

집합 (Sets)

집합의 기본 표현과 원소와의 관계 표현

집합은 원소라 불리우는 서로 구별할 수 있는 객체들의 모임이다. 만약 객체 x가 집합 S에 속한다면 $x \in S$로 표현하며, 반대로 소속되지 않는다면, $x \notin S$로 표현한다.

집합은 보통 “{”, “}” 사이에 소속된 원소들을 나열하여 표현하며, 이때 같은 원소가 중복되어 소속 될 수 없으며, 만약 중복이 존재할 경우, 2개 이상부터는 없는걸로 취급해도 된다. 중복을 허용하는 집합은 중복집합(multiset)이라고 부른다.

집합 내의 원소들은 정렬되어 있을 필요없다.

만약 두 집합에 소속된 원소들이 완전 일치한다면, $A=B$로 표현하며, 예를 들어 ${1,2,3,1}={1,2,3}={3,2,1}$로 표현 된다.

다음은 자주 사용되는 집합의 표기법들이다.

• $\O$는 아무 원소도 소속되지 않은 빈 집합을 의미하며, 공집합이라고 부른다.
• $\Z$는 모든 정수들로 이루어진 집합을 의미한다. {…-2,-1, 0,1,2,…} 정수집합이라고 부른다.
• $\R$은 모든 실수들로 이루어진 집합을 의미한다. 실수 집합이라고 부른다.
• $\N$은 모든 자연수들로 이루어진 집합을 의미한다. {0,1,2,3 …}, 자연수 집합이라고 부른다.

집합 간의 관계 표현

집합 A에 속한 원소들이 모두 집합 B에 속할 때, $A \subseteq B$로 표현하며, A는 B의 부분집합이라고 표현한다.

$A\subset B$는 집합 A에 속한 원소들이 모두 집합 B에 속하면서 동시에 $A \neq B$인 경우에 사용한다. (즉, $B \nsubseteq A $인 경우)

$A \subseteq B$이면서 $B \subseteq A$인 경우는 $A=B$이다.

$A \subseteq B$이며, $B \subseteq C$인 경우는 $A \subseteq C$이다.

모든 집합 A에 대해서 공집합 $\O \subseteq A$이다.

집합은 다른 집합을 통해서 표현될 수 있다. 예를 들어 $\Z$를 이용해 다른 집합을 표현하는 예시로, ${x:x\in \Z\ and\ x/2\ is\ an\ integer}$

이때 “:”(colon)는 x의 성질을 나타내며, 표기에 따라 “

“로 표현되기도 한다.

집합 연산

A와 B의 교집합(intersection)은 $A \cap B$로 표현하며, 집합 ${x:x\in A\ and\ x \in B}$, 즉 A와 B에 둘 다 존재하는 원소들의 집합을 의미한다.

A와 B의 합집합(union)은 $A \cup B$로 표현하며, 집합 ${x:x \in A\ or\ x\in B}$, 즉 A 또는 B에 존재하는 원소들의 집합을 의미한다.

A에 대한 B의 차집합(difference 또는 relative compliment)는 $A-B$로 표현하며, 집합 ${x: x \in A\ and\ x\notin B}$, 즉 A에는 존재하지만, B에는 존재하지 않는 원소들의 집합을 의미한다.

집합 연산에 의한 법칙

또한 집합 연산에 따른 다음과 같은 법칙들이 존재한다.

• 공집합 법칙 (Empty set laws)
  \(A \cap \O=\O\\ A \cup \O=A\)

• 멱등 법칙 (Idempotency laws)
  \(A \cap A=A\\ A \cup A = A\)

• 교환 법칙 (Commutative laws)
  \(A \cap B = B\cap A\\ A \cup B = B \cup A\)

• 결합 법칙 (Associative laws)
  \(A\cap(B\cap C)=(A \cap B)\cap C\\ A \cup (B\cup C)=(A \cup B) \cup C\)

• 분배 법칙 (Distributive laws)
  \(A \cap(B\cup C)= (A \cap B)\cup (A \cap C)\\ A \cup (B \cap C)=(A\cup B)\cap(A\cup C) \label{law:Distributive} \tag{B.1}\)

• 흡수 법칙 (Absorption laws)
  \(A \cap (A \cup B)=A\\ A \cup (A \cap B)=A\)

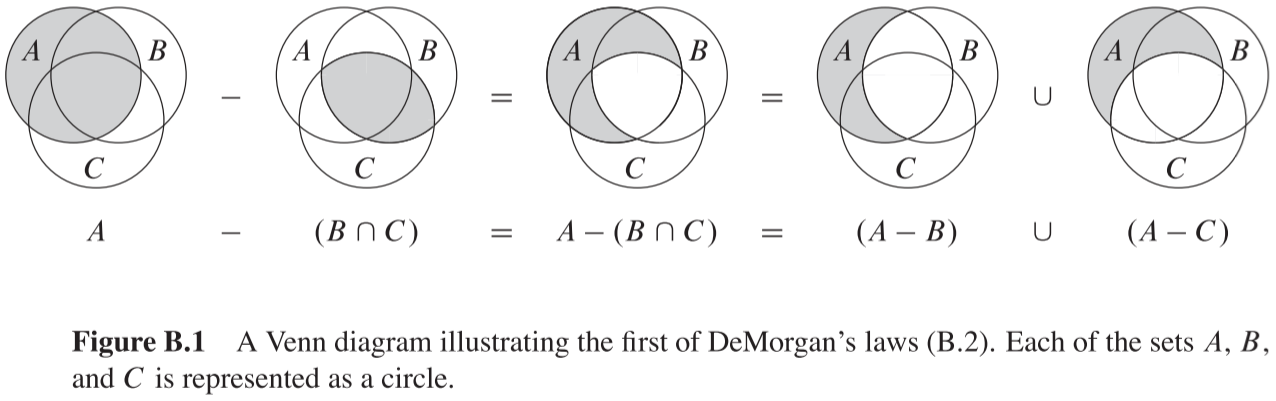
• 드 모르간의 법칙 (DeMorgan’s laws) (Figure B.1)
  \(A-(B\cap C)=(A-B)\cup(A-C)\\ A-(B\cup C)=(A-B)\cap(A-C) \label{law:Demorgan} \tag{B.2}\)

집합 연산 시, 많은 경우 아래와 같이 벤 다이어그램(Venn diagram)으로 표현하곤 한다.

모든 집합들은 전체 집합 U의 부분집합이며, 이 전체 집합 U는 해당 집합의 특징에 따라 다르다. 예를 들어 정수로만 이루어진 집합들은 모두 정수 집합 $\Z$의 부분집합이며, 이때 $\Z$는 전체집합 U가 된다.

전체집합 U에 대한 A의 차집합, 즉 $U-A={x:x\in U\ and\ x \notin A}$는 $\overline{A}$로 표현되며, 여집합(complement)라고 한다.

집합 A가 전체집합 U의 부분집합 일 때, 다음과 같은 법칙이 성립한다.
\(\overline{\overline{A}}=A\\ A\cap\overline{A}=\O\\ A\cup\overline{A}=U\)
또한, $B,C\subseteq U$일 때, 드모르간의 법칙을 활용해 다음과 같은 법칙이 성립한다.
\(\overline{B \cap C}=\overline{B}\cup\overline{C}\\ \overline{B \cup C}=\overline{B}\cap\overline{C}\)

서로소 집합(disjoint set)

두 집합 A와 B의 교집합이 공집합일 때, 즉, $A\cap B = \O$일 때 A와 B를 서로소 집합(disjoint set)이라고 한다.

특정 집합 S를 i개의 집합으로 나눈 것의 공집합이 아닌 i번째 집합을 $S_i$라 하며 분할(partion)이라 부르자, 이 집합들의 집합을 집합족이라고 하며, 집합족 P라고 하자.

• 집합족 P의 원소집합들은 모두 서로 간에 서로소(pairwise disjoint)이다. 즉 집합족 P는 서로소 집합족이다. $S_i \cap S_j = \O$
• 집합족 P의 원소집합들 모두의 합집합은 S이다. 즉 $S=\bigcup_{S_i\in P}S_i$

카디널리티(cardinality)

집합의 원소의 갯수를 크기(size) 또는 카디널리티(cardinality, 농도)라고 부르며 $

S

$로 표현된다.

유한한 집합의 크기 n에 따라 n-set 집합이라고 불리우며, n이 1일 경우 싱글톤(singleton)이라고 부른다. 해당 집합이 어떤 집합의 부분집합(subset)이고, 크기가 n일 겨우 n-subset 집합이라고 부른다.

두개의 집합의 원소가 서로 1대1 대응 관계라면 같은 크기를 가진다는 의미이며, 공집합 $\O$의 크기, $

\O

$는 0이다.

집합의 크기는 자연수로 표현되면, 유한한 크기이며, 그렇지 않다면 무한한 크기를 가진다.

자연수 집합 $\Z$과 1대1 대응되는 무한 크기 집합을 가산 무한(countably infinite) 크기 집합이라고 하며, 실수 집합 $\R$같 은경우 불가산(uncountable) 무한 크기 집합니다.

유한한 크기의 두 집합 A, B에 대해
\(|A \cup B|=|A|+|B|-|A \cap B| \label{eq:setUnionSize} \tag{B.3}\)
이 성립되므로, $|A\cup B|\leq |A|+|B|$이며, A와 B가 서로소라면 $|A\cap B|=0$이고,$|A \cup B|=|A|+|B|$이다. 또한 이때, $A \subseteq B$ 일 때, $|A| \leq |B|$이다.

n개의 크기를 가진 집합 S의 모든 부분집합의 경우의 수는 $2^n$이며, 이들을 집합 S의 power set(멱집합)이라고 한다.

파워 셋에는 공집합과 집합 S를 포함하며, 예시를 들자면, $S = {a,b}$의 파워셋은 ${\O, {a}, {b}, {a,b} }$ 으로 $2^{

S

}$인 4개이다.

순서쌍(ordered pair)

순서쌍(ordered pair)는 집합과 비슷하지만, 원소들이 정렬된 형태이며, 두개의 원소 a,b 순으로 포함된 순서쌍은 (a, b)로 표현된다.

이는 집합과 달리 (b, a)와 다른 순서쌍이며, a, b를 각각 n번째 성분(entry), 또는 n번째 좌표(coordinate)라고 부른다.

순서쌍 (a, b)를 집합론적으로 표현할 시, ${{a}, {a,b}}$로 표현하며 이는 두 순서쌍의 n번째 성분이 모두 다를 경우, 둘은 다른 순서쌍이라는 성질에 의해서이다.

예를 들어, (a, b)와 (b,a)를 각각 집합 ${{a}, {b}}, {{b},{a}}$로 표현하면, 이 둘은 집합 관점에서는 서로 같다는 의미이나, 순서쌍에서는 그렇지 않으므로 적절치 않다.

위의 집합 표현 시 (a, b)와 (b, a)는 각각 집합 ${{a}, {a,b}}, {{b}, {b,a}}$로 표현되므로 집합 표현에서도 서로 다르고, 순서쌍 표현에서도 서로 다르게 된다.

• 이를 쿠라토프스키의 순서쌍 정의라고 한다. (https://ko.wikipedia.org/wiki/%EC%88%9C%EC%84%9C%EC%8C%8D)

곱집합(Cartesian product)

두 집합 A와 B의 곱집합(Cartesian product)은 $A \times B$로 표현되며, 첫번째 성분은 A의 원소이며, 두번째 성분은 B의 원소인 순서쌍 들의 모든 경우의 수들의 집합이다. 수식으로 표현하자면 $A\times B={(a,b):a\in A\ and\ b \in B}$이며, 예시로 ${a,b} \times {a,b,c}={(a,a),(a,b),(a,c),(b,a),(b,b), (b,c)}$이다.

유한한 두 집합 A와 B의 곱집합의 카디널리티(cardinality)는 다음과 같이 표현된다.
\(|A\times B|=|A|\cdot |B| \label{eq:setABCartProd} \tag{B.4}\)
n개의 집합 $A_1,A_2,\dots,A_n$의 곱집합은 n-튜플들의 집합이며, 이때 n-튜플 하나는 n 길이의 유한 수열(sequence)로도 볼 수 있으며, 다음과 같이 표현된다.

• 튜플(tuple): 유한한 크기의 요소들의 순서있는 열거

\[A_1\times A_2\times\cdots \times A_n=\{(a_1,a_2,\cdots,a_n):a_i \in A_i\ for\ i=1,2,\cdots,n\}\]

이때의 카디널리티는 $

A_1\times A_2\times \cdots \times A_n

=

A_1

\cdot

A_2

\cdots

A_n

$이다.

하나의 유한한 크기의 집합 A의 n 반복(n-fold) 곱집합은 $A^n$의 카디널리티를 가진다.