avatar

풀스택 웹🌐 개발자 지망생 🧑🏽‍💻
➕ 인공지능 관심 🤖

Categories

Recent views

  • 1
  • 2
  • 3
  • 4
  • 5

알고리즘 수학 기본-그래프

  1. 유향 그래프와 무향 그래프
  2. 그래프 용어
  3. 기타 여러 종류의 그래프

알고리즘을 위한 수학 - 그래프(graphs)

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

일부 표기나 개념이 기존의 수학과 다를 수도 있으므로, 여기서 배운 내용은 단순 해당 책(Introduction to Algorithm, 3rd, Cormen)의 부록으로 취급해야한다.

이 장에서는 그래프(graphs)의 표기법, 정의, 속성 같은 기본적인 것만 배운다.

앞서 올린 포스트 집합(sets)와 관계(relations)에 대한 글을 읽고 오는 것을 추천한다.

유향 그래프와 무향 그래프

유향 그래프와 무향 그래프의 정의

유향 그래프(directed graph, digraph) G는 유한한 집합 V와 V의 원소 간의 이항관계 E의 쌍, (V, E)이다.

집합 V는 G의 정점 집합(vertex set)이라고도 불리우며, 이들의 원소들을 정점들(vetices)이라고 부른다.

집합 E는 G의 간선 집합(edge set)이라고 불리우며, 이들의 원소들을 간선들(edges)라고 부르며, 순서가 존재하는 쌍으로 표현한다. (예시: (1,2), (2,2))

Figure 1의 (a) 그래프가 유향 그래프의 예시로, 간선은 화살표, 정점은 숫자가 적힌 원으로 표현하였다. 자기 자신으로 회귀하는 2번 정점과 같은 간선 또한 그래프에 나타날 수 있다.

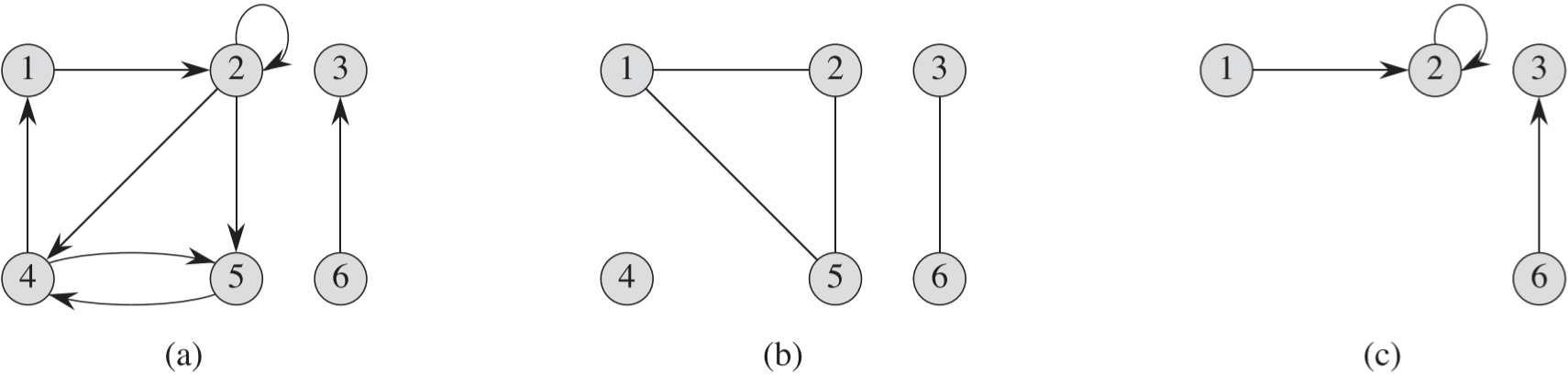
무향 그래프(undirected graph) G는 간선 집합 E가 유향 그래프와 달리 순서가 없는 쌍, 즉 원소가 둘인 집합을 간선으로 가지고 있지만, 표기는 동일하게 (u, v) 처럼 한다. 이는 즉, 두 그래프간의 선분의 방향성이 존재하지 않다는 것이며, 양방향이기도 하다는 의미이다.

이때, 무향 그래프는 유향 그래프와 달리 자기 회귀(self-loop) 간선이 존재하면 안되며, 따라서 간선의 두 원소는 서로 다른 정점이어야 한다.

유향 그래프에서 정점 A의 이웃(neighbor) 정점은 정점 A와 해당 이웃 정점으로 오는 간선과 가는 간선이 둘다 존재하는 정점이다.

무향 그래프에서 정점 A의 이웃(neighbor) 정점은 정점 A와 간선이 존재하는 정점이다.

무향 그래프와 유향 그래프의 전환

무향 그래프 $G=(V,E)$를 유향 그래프로 바꾸려면, G의 간선 집합 E의 간선들 (u,v)를 모두 유향 간선 (u, v)와 (v, u)로 바꾸면 된다.

반대로 유향 그래프 $G=(V, E)$를 무향 그래프로 바꾸려면, 자기 회귀(self-loop) 간선 (u, u)는 모두 삭제하고, 간선들 (u, v)을 중복이 존재하지 않도록 무향 간선 (u, v)으로 바꾸면 된다. 즉 (u, v) 간선과 (v, u) 간선이 둘다 존재한다면 무향 간선 (u, v)하나로만 바꾼다.

그래프 용어

무향 그래프와 유향 그래프의 정의들은 거의 유사하지만 일부 정의에서 다르다.

부속과 인접(incident, adjacent)

유향 그래프에서는 선분 (u, v)을 정점 u에서 부속 출발(incident from) 또는 떠나서(leaves) 정점 v에 부속 도착(incident to) 또는 도착하는 선분이라고 부른다.

유향, 무향 그래프에서 선분 (u, v)를 정점 u, v에 부속(incident)한다고 표현하며, 정점 u와 v가 서로 인접(adjacent)하다고 표현한다.

무향 그래프와 달리 유향 그래프에서는 정점 간의 인접 관계가 비대칭인데, 예를 들어 Figure 1 (a)에서 2번 정점은 1번 정점과 인접하지만 1번 정점은 2번 정점과 인접하지 않다. 즉, 유향 그래프에서 어떤 정점 A 입장에서 B와의 인접은 A 정점으로 도착할 수 있는 선분을 B 정점이 가지고 있는가를 의미한다.

차수와 고립(degree, isolated)

무향 그래프에서의 정점의 차수(degree)는 해당 정점에 부속된 간선들의 수이다. 예를 들어 Figure 1 (b)의 정점 2는 차수가 2이며, 정점 4처럼 차수가 0인 정점을 고립된(isolated) 정점이라고 한다.

유향 그래프에서 진출 차수(outdegree)는 해당 정점에서 나가는 간선의 수를 의미하며, 진입 차수(indegree)는 반대로 들어오는 간선의 수를 의미한다.

유향 그래프에서 정점의 차수는 진출 차수와 진입 차수의 합을 의미한다. Figure 1 (a)의 정점 2의 진입 차수는 2, 진출 차수는 3이므로 정점 2의 차수가 총 5이며, 이때 자기회귀 선분은 2번 더해진다는 것을 알 수 있다.

경로와 간단 경로(path, simple path)

시작 정점 $u$에서 도착 정점 $u’$로 가는 경로(path)는 정점들로 이뤄진 수열 $<v_0,v_1,v_2,\cdots,v_k>$이며, 이때 $u=v_0,u’=v_k$이고, i가 $1,2,\cdots, k$일 때, 선분 $(v_{i-1},v_i)$는 그래프의 선분 집합 E에 포함된다. 자기자신으로 가는 경로는 길이가 0인 경로이다.

경로의 길이(length) k는 경로 내의 선분들의 수이며, 경로가 존재한다는 의미는, 해당 경로를 통해 시작 정점에서 도착 정점으로 도착 가능하다는 의미이다.

이때, 경로의 정점들이 중복이 없다면, 간단 경로(simple path)라고 부른며, 예를 들면 <1,2,5,4> 경로는 간단 경로, <2,5,4,5>는 간단하지 않은 경로이다.

부분 경로(subpath)는 경로 수열의 일부분의 연속된 수열이며, 경로와 마찬가지로 다음 정점과 간선으로 이어져있어야 한다.

사이클(cycle)

시작 정점과 도착 정점이 같은 길이가 1이상의 경로, 즉 $v_0=v_k$이면서, 최소 하나의 간선을 포함한 경로는 사이클(cycle)이라고 하며, 시작지점 $v_0$를 제외하고 나머지 정점들이 전부 중복이 없다면 간단 사이클이라고 부른다. 자기회귀는 길이가 1인 사이클이다.

서로 다른 두 경로는 같은 사이클을 형성할 수 있는데, 예를 들어 Figure 1 (a)의 경로 <1,2,4,1>은 경로 <2,4,1,2>와 다른 경로이되 같은 사이클이다.

수학적으로 표현하면 경로 $<v_0,v_1,v_2,\cdots,v_{k-1},v_0>$와 경로 $<v’0,v’_1,v’_2,\cdots,v’{k-1},v’0>$에서 $v’_i=v{(i+j)\mod k}$를 만족하는 i가 존재한다면 같은 사이클이다.

자기회귀가 없는 유향 그래프를 간단 그래프라고 한다.

무향 그래프에서는 경로의 길이가 3 이상인 경로, 즉 중간 경유지가 존재하는 경로만 사이클로 인정된다.

사이클이 존재하지 않는 그래프를 acyclic 그래프라고 한다.

연결 그래프(connected graph)와 연결 요소 (connected component)

무향 그래프에서 모든 정점들이 고립되지않았다면, 연결(connected) 그래프라고 하며, 그래프의 연결 요소(connected component)는 정점 A에서 B로 도달 가능한 가? 관계의 동치류들을 의미한다. 예를 들어 Figure 1 (b)에는 {1,2,5}, {3,6}, {4} 총 3개의 연결 요소가 존재한다. 연결 그래프에는 연결 요소가 1개 밖에 없다.

연결 요소의 선분들은 연결 요소 내 정점만 연결되있는 선분이다, 즉 선분 (u, v)에서 u와 v는 언제나 같은 연결 요소 내에 존재해야 한다.

만일 방향 그래프 내의 모든 쌍의 정점들이 서로 도달 가능하다면 강연결 그래프(strongly connected)가 된다.

방향 그래프의 강연결 요소(strongly connected components)는 상호 도달 가능한 관계에 대한 정점으로 이루어진 동치류들이다. 강연결 요소가 한 그래프에 하나만 존재한다면 강연결 그래프가 된다.

Figure 1 (a)에는 {1,2,4,5}, {3}, {6}, 총 3개의 강연결 요소가 존재한다.

동형 그래프 (isomorphic graph)

두 그래프 $G = (V, E)$와 $G’=(V’,E’)$에서, 간선 $(u,v) \in E$일 때, 간선 $(f(u), f(v)) \in E’$ 인 전단사 함수 $f:V \rightarrow V’$ 가 존재할 시, 서로 동형(isomorphic) 그래프라고 한다. 즉, 두 그래프가 정점의 번호만 다르고 모양이 같을 때 동형 그래프라고 한다.

Figure 2 (a)의 위 그래프와 아래 그래프는 정점의 번호만 1,2,…,6와 u,v,…,z로 서로 다를 뿐, 그림 상의 정점의 위치를 조정하고 그에 따라 선분도 조정하면 동일한 모형의 그래프가 된다. 예를 들어 $f(1)=u, f(2)=v … f(6)=z$ 같은 식으로 대입해보면 된다.

하지만 Figure 2 (b) 오른쪽의 상하 그래프는 그리하여도 모양이 다르게 되므로 동형 그래프가 아니다.

부분 그래프 (subgraph)

만약,두 그래프 $G = (V, E)$와 $G’=(V’,E’)$에서, $V’ \subseteq V, E’ \subseteq E$일 경우, $G’$를 $G$의 부분 그래프(subgraph)라고 표현한다.

부분 그래프에서는 $V’$를 이용해 식 $E’= {(u,v) \in E:u,v \in V’}$를 이용해 $E’$ 또한 도출할 수 있다.

예를 들어 Figure 1 (c)의 그래프는 Figure 1 (a)의 부분 그래프이며, $V’={1,2,3, 6}$이므로 $E’={(1,2), (2,2), (6,3)}$임을 알 수 있다.

기타 여러 종류의 그래프

완전 그래프 (complete graph)

소속한 모든 정점이 다른 모든 정점과 연결된 무향 그래프를 완전그래프라 한다.

이분 그래프 (bipartite graph)

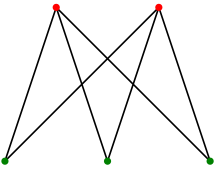
이분그래프는 정점을 두 집합으로 나눈 뒤, 같은 집합의 정점 간에는 간선이 존재하지 않는 그래프를 의미한다.

포레스트(forest)와 트리((free) tree)

사이클과 고립 정점이 없는 무향 그래프, 즉 acyclic 무향 연결 그래프(acyclic undirected connected graph)를 트리(tree) 또는 자유 트리(free tree)라고 한다.

하나 이상의 트리가 모인 무향 그래프, acyclic 무향 그래프를 포레스트(forest)라고 한다.

포레스트 그래프는 시작 정점과 도착 정점이 같은 경로가 2개 이상 존재하지 않는다.

방향 acyclic 그래프(directed acyclic graph)는 줄여서 DAG 라고도 부른다.

다중 그래프(multigraph)

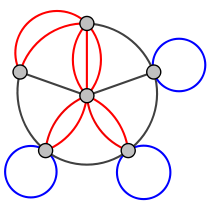
어떤 두 정점 간의 간선이 중복되어 여러개 있거나, 자기 회귀(self-loop)가 존재하는 무향 그래프이다.

하이퍼그래프 (hypergraph)

그래프 내의 정점 간의 집합을 형성한 뒤, 해당 집합 간의 간선이 존재하는 그래프, 기존의 그래프 알고리즘을 활용 가능하다.

수축 (contraction)

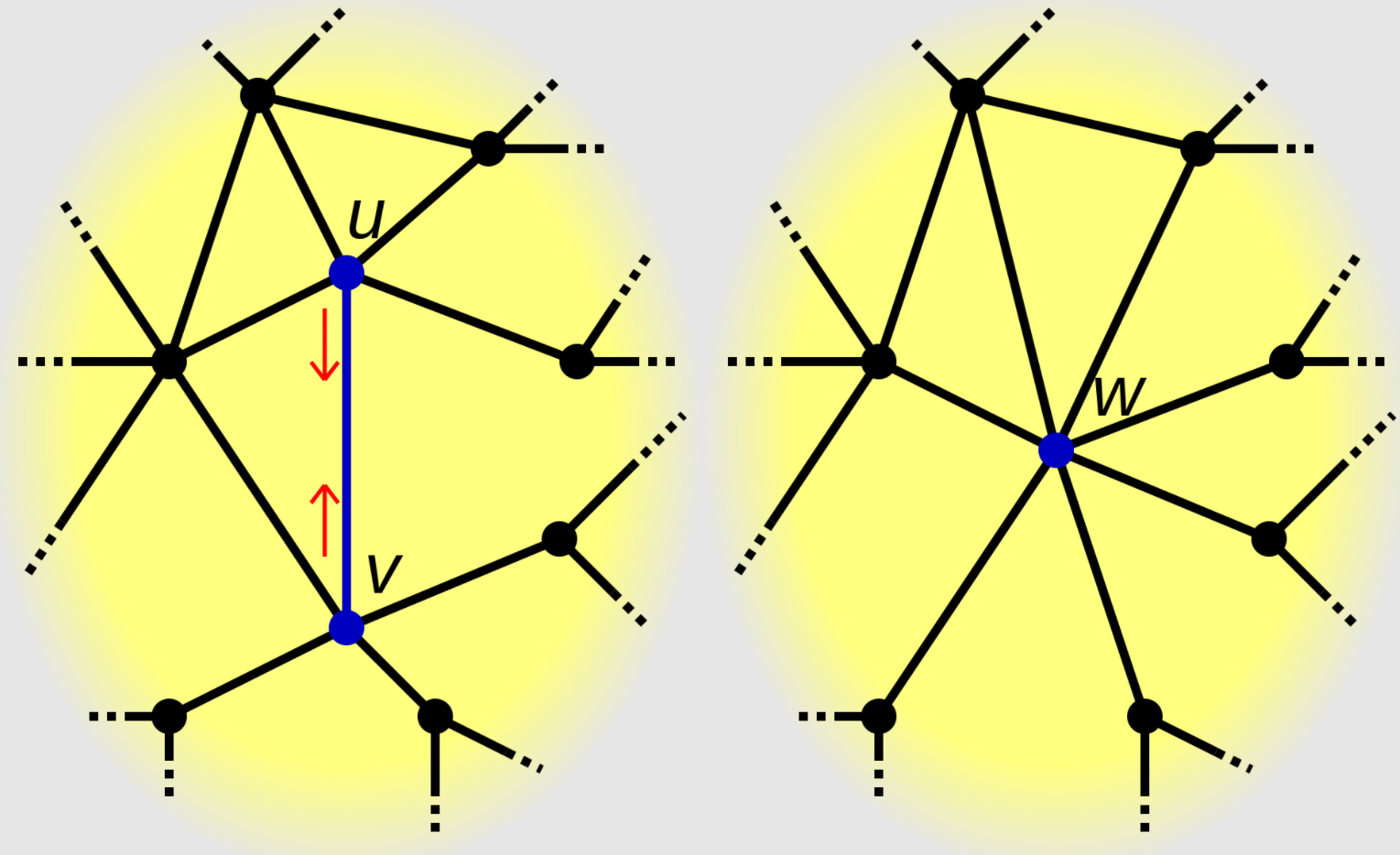
어떤 무향 그래프의 G에 대해 새로운 정점들의 집합 $V’=V-{u,v}\cup {x}$을 만들고, 정점 u와 v를 이어주는 모든 간선을 삭제한 뒤, u와 v 정점에 인접한 정점들을 새로 만든 정점 x과 연결하는 행위.

쉽게 말해 두 정점과 그 사이의 간선을 하나의 새로운 정점으로 합치는 것이다.