avatar

풀스택 웹🌐 개발자 지망생 🧑🏽‍💻
➕ 인공지능 관심 🤖

Categories

Recent views

  • 1
  • 2
  • 3
  • 4
  • 5

알고리즘-하

  1. Array 활용
  2. 기하
  3. 기타

알고리즘 전문

Array 활용

미트 인 더 미들 알고리즘 (Meet in the middle Algorithm)

  • 분할 정복(Divide and Conquer algorithm)과 비슷하게 주어진 input을 2개로 나눈 뒤, 두개의 연산 결과를 이용해 값을 찾아내는 알고리즘
  • 예를 들어 n개의 수의 부분집합을 찾아내는 것은 시간 복잡도 O(2^n)의 연산이 필요하지만 20개씩 2개의 부분집합을 찾아낸 뒤 합치는 것으로 O(2^(n/2)) 으로 줄일 수 있다.

투 포인터 알고리즘 (Two Pointers Algorithm)

  • 정렬된 배열 내에서 값의 쌍을 탐색하는 알고리즘
# 수의 배열에서 합이 sumX가 되는 수의 쌍의 갯수를 구하기
# (i, j) 와 (j, i)는 하나로 간주한다.
import sys
input = sys.stdin.readline
listSize = int(input())
nums = list(map(int, input().split()))
sumX = int(input())
nums.sort()
answer = 0
start = 0
end = listSize -1
while(start < end):
	sumOfPair = nums[start] + nums[end]
    if sumOfPair > sumX:
	    end -= 1
    elif sumOfPair < sumX:
        start += 1
    else:
        start += 1
        end -= 1
        answer += 1
print(answer)
  • 주로 배열의 정렬과 두 포인터 인덱스를 기준으로 만든 배열을 이용해 문제를 해결한다.

스위핑

  • 배열의 값을 차례대로 처리하면서 만든 값을 비교해가며 다음 값을 구하는 방법

  • 동적 계획법(Dynamic Programming, DP)과 비슷하나 보통 먼저 정렬을 한 뒤에 처리를 하는 방법.

기하

Convex Hull

  • 보통 좌표가 주어지고 해당 좌표로 다각형을 만드는 알고리즘

CCW(Counter Clock Wise)

  • 벡터의 외적(Cross Product)를 이용해 하나의 정점을 기준으로 다른 점과 점 간의 상대적 위치를 알아낼 수 있음
세점 (a, b, c)가 존재할 때
벡터의 외적 = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x)
또는
벡터의 외적 = (a.x * b.y + b.x * c.y + c.y * a.y) - (a.y * b.x + b.y * c.x + c.y * a.x)

벡터의 외적이 양수이면 ABC 순으로 반시계반대 방향으로 벡터가 변화,(ab벡터가 ac벡터보다 더 반시계방향으로 꺾여있음)
음수이면 ABC 순으로 시계방향으로 벡터가 변화,(ab벡터가 ac벡터보다 더 시계방향으로 꺾여있음)
0이면 평행임을 의미한다.(ab,ac벡터가 같은 방향임)

B
C
A
위 예시로 따지면 A,B,C 순서로 시계반대방향 관계(양수), A,C,B 순서로 시계방향(음수) 관계이다.

  • 두 벡터의 시작점을 맞추고 그 둘의 각도를 통해 두 벡터로 만든 삼각형 넓이 구하기 가능
  • 각 꼭지점을 반시계방향으로 점을 향한 벡터를 저장하여 단순 다각형 저장 가능
  • CCW 생성 가능 , sin∂ 방향으로 외적의 음수 양수를 정의해야함 A, B벡터와 B, A벡터는 부호가 다름
  • a,A가 시작점
  • 음수 양수 뿐만 아니라 나오는 값의 절대값도 다르지만 이것으로 각도나 위치 등을 판단하지 말자,
    • 좌표가 다름에도 같은 값이 나올 때가 있다.
    • (A:(0,0), B:(0,1) 이 일 때, C:(1,0) 과 C:(1,1)을 넣어보면 똑같이 -1이 나온다. )
int CCW(ax,ay,bx,by,cx,cy){
    int t = (bx-ax)*(cy-ay)-(by-ay)*(cx-ax);
    if (t>0) return 반시계;
    if (t<0) return 시계;
    return 일직선;
}

그라함 스캔 알고리즘

  • 시간 복잡도 $O(n \log n)$
import sys, functools
input = sys.stdin.readline
def ccw(a, b, c):
    t = (b['x']-a['x'])*(c['y']-a['y']) - (c['x'] - a['x'])*(b['y'] - a['y'])
    if t > 0:
        return 1
    elif t < 0:
        return -1
    else :
        return 0
def comp(a, b):
    global firstPoint
    return -ccw(firstPoint,a,b)
def comp0(a, b):
    if a['y'] == b['y']:
        return 1 if a['x'] > b['x'] else -1 
    else:
        return 1 if a['y'] > b['y'] else -1
# def getFuther(std, a, b):
#    lenToA = (a['x'] - std['x'])**2 + (a['y'] - std['y'])**2
#    lenToB = (b['x'] - std['x'])**2 + (b['y'] - std['y'])**2
#    return a if lenToA > lenToB else b
pointNum = int(input())
points = []
firstPoint = {'x':0, 'y':9999099}
for _ in range(pointNum):
    x, y = map(int, input().split())
    points.append({'x':x,'y':y})
points.sort(key=functools.cmp_to_key(comp0))
firstPoint = points[0]
points.sort(key=functools.cmp_to_key(comp)) # cmp to key function to use comparer
st = [points[0], points[1]]
for point in points[2:]:
    while(len(st) >=2):
        if (ccw(st[-2], st[-1], point) > 0):
	        break
        st.pop()
    st.append(point)
print(len(st))

기타

SCC (Strongly Connected Component, 강한 연결 요소)

  • 방향 그래프에서 집합 내에서 서로 왕복가능한 정점들의 최대 크기 집합을 의미함.
  • 한 SCC 내의 모든 정점은 다른 모든 정점에 들럿다가 다시 돌아올 수 있다.
  • 자기 자신으로 돌아올 수 있는 1개짜리 정점도 포함한다.

색칠한 부분이 각각의 SCC이다. https://www.acmicpc.net/problem/2150 (백준 알고리즘)

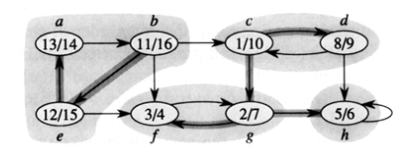
  • 그래프가 주어졌을 때 SCC 집합의 존재 여부나 갯수, 소속 집합 정보 등이 필요할 때가 많다.

  • 주로 DFS(Depth first search, 깊이 우선 탐색)기반의 알고리즘을 사용한다.

코사라주 알고리즘

  • 방향 그래프, 해당 방향그래프의 역방향 그래프, 스택을 이용하여 SCC를 구하는 알고리즘
  • SCC는 한 노드에서, 다른 노드로 어느 방향이로든 갈 수 있으며 역방향으로 바꾸어도 마찬가지인 것을 이용한 알고리즘
  • 아래의 타잔 알고리즘 보다 구현과 생각이 쉽지만 메모리를 좀더 먹는다.
  • 시간 복잡도는 O(V+E)
import sys
sys.setrecursionlimit(987654321)
# kosaraju algorithm
input = sys.stdin.readline
nodeCount, edgeCount = map(int, input().split())
edges = [[i] for i in range(nodeCount+1)]
revEdges = [[i] for i in range(nodeCount+1)]
visited = [False for _ in range(nodeCount+1)]
st = []
SCCs = []
SCCIdx = 0
for _ in range(edgeCount):
    fr, to = map(int, input().split())
    edges[fr].append(to)
    revEdges[to].append(fr)

def dfs(i):
    visited[i] = True
    for node in edges[i]:
        if not visited[node]:
            dfs(node)
    st.append(i)

def func(node, SccIdx):
    visited[node] = True
    SCCs[SccIdx].append(node)
    for adj in revEdges[node]:
        if not visited[adj]:
            func(adj, SCCIdx)

# 정방향 그래프를 돌며 dfs 함수가 끝날때 스택에 집어넣는다.
# 결과적으로 가장 처음에 dfs를 실행한 노드가 스택에 마지막으로 들어가고, SCC의 대표노드가 된다.
for i in range(1, nodeCount+1):
    if not visited[i]:
        dfs(i) 

visited = [False for _ in range(nodeCount+1)]

# 스택에 마지막에 들어간 노드가 제일 먼저 튀어나오며 역방향으로 갈 수 있는 모든 노드를 찾아 SCC로 포함시킨다.
# 이때 SCC에 포함될 수 없지만 대표노드에 연결되었던 노드는 역방향 그래프로 바뀌었으므로 진입할 수 없어 SCC에 들어가지지 않는다.
# 역방향이 되어 대표노드에서 갈 수 있게된 노드는 이전 dfs 때 스택에 나중에 들어가 이번에 먼저 튀어나오므로 visited가 True가 되있어 들어가지 않는다.
while st:
    now = st.pop()
    if not visited[now]:
        SCCs.append([])
        func(now, SCCIdx)
        SCCIdx += 1

for SCC in SCCs:
    SCC.sort()

SCCs.sort()
print(len(SCCs))

for SCC in SCCs:
    SCC.append(-1)
    [print(i, end=' ') for i in SCC]
    print()

타잔 알고리즘

  • 위상정렬을 기반으로 하는 SCC 알고리즘
  • 스택에 노드를 집어넣고, 가장 처음 집어넣은 노드를 대표노드로 삼은 뒤, dfs를 돌려 갈 수 있는 노드를 모두 스택에 넣은 후, dfs가 대표노드로 돌아오면 처음 설정한 대표노드가 나올때 까지 pop하여 해당 노드들을 같은 SCC로 묶는 원리.
  • 코사라주 알고리즘 보다 메모리적으로 효율적이다.
  • 시간 복잡도는 똑같이 O(V+E)
import sys
sys.setrecursionlimit(987654321)
# tarjan algorithm
input = sys.stdin.readline
nodeCount, edgeCount = map(int, input().split())
edges = [[i] for i in range(nodeCount+1)]
discover = [-1 for _ in range(nodeCount+1)]
SCCs = [-1 for _ in range(nodeCount+1)]
discoverIdx = 0
SCCIdx = 0
st = []
res = []
def dfs(now):
    global discoverIdx, SCCIdx
    discover[now] = discoverIdx
    discoverIdx += 1
    discoverNow = discover[now]
    st.append(now)
    for adj in edges[now]:
        if discover[adj] == -1:
            discoverNow = min(discoverNow, dfs(adj))
        elif SCCs[adj] == -1:
            discoverNow = min(discoverNow, discover[adj])
    if discoverNow == discover[now]:
        SCC = []
        while True:
            target = st.pop()
            SCCs[target] = SCCIdx
            SCC.append(target)
            if target == now: break
        SCC.sort()
        res.append(SCC)
        SCCIdx += 1
    return discoverNow
for _ in range(edgeCount):
    fr, to = map(int, input().split())
    edges[fr].append(to)

for i in range(1, nodeCount+1):
    if discover[i] == -1:
        dfs(i)

res.sort()
print(len(res))
for SCC in res:
    SCC.append(-1)
    [print(i, end=' ') for i in SCC]
    print()

avl tree 알아보기

lcp : https://blog.naver.com/dark__nebula/220419358547

suffix array : https://plzrun.tistory.com/entry/Suffix-Array-ONlogNlgN%EA%B3%BC-ONlogN-%EA%B5%AC%ED%98%84-%EB%B0%8F-%EC%84%A4%EB%AA%85