avatar

풀스택 웹🌐 개발자 지망생 🧑🏽‍💻
➕ 인공지능 관심 🤖

Categories

Recent views

  • 1
  • 2
  • 3
  • 4
  • 5

알고리즘-중

  1. 02 알고리즘 복잡도
    • 03 비트연산
      • 완전 검색으로 시작하기
        • 2. 조합적 문제
          • 3. 부분집합
            • 4. 조합(Combination)
              • 2. 병합 정렬
                • 3. 퀵 정렬
                  • 05 백트래킹
                  • 06 그래프의 기본과 탐색
                  • 07 그래프의 최소 비용 문제
                  • 08 문자열 탐색
                  • 09 동적 계획법의 소개
                    • 10 동적 계획법의 적용
                      • 11 동적 계획법의 활용
                        • 12 NP-Complete
                          • 13 근사 알고리즘
                            • 14 정수론과 최적화

                              알고리즘 응용

                              02 알고리즘 복잡도

                              알고리즘

                              • 유한한 단계를 통해 문제를 해결하기 위한 절차나 방법

                              • 주로 컴퓨터 용어로 쓰이며, 컴퓨터가 어떤 일을 수행하기 위한 단계적 방법

                              • 어떠한 문제를 해결하기 위한 절차, 알고리즘을 쓰면 메모리, 재사용성, 성능 측면에서 유리

                              • 1~100까지의 합을 구하는 방법: 공식 사용 vs 일일이 하기 정도의 차이

                              • 실행에 필요한 자원을 분석하여 효율성 제시, 복잡도(Complexity)로 표현, 높을수록 안좋음

                                   1) 공간적 효율성 : 얼마나 많은 메모리 공간을 요하는가?
   2) 시간적 효율성 : 얼마나 많은 시간을 요하는가?
   - 하드웨어, 소프트웨어 환경에 따라 처리시간 달라짐, 시간으로는 표현 힘듬
   - 보통 알고리즘 효율성은 입력크기가 너무 클때 문제가 됨
                                • 같은 일을 해도 알고리즘에 따라 300년걸릴 일일을 5분만에 끝낼 수 있음

                              점근적 표기

                              • 시간 (또는 공간) 복잡도의 점근적 표기

                                • 입력 크기에 대한 함수로 표기, 함수는 다항식

                                • 단순한 함수로 표현하기 위해 점근적 표기(Asymptotic Notation) 사용
                                  1. O(Big-Oh) 표기

                                • 복잡도의 점근적 상한(즉 효율이 최악의 상황일 때의 표기)
                                • 다항식의 최고차항만 계수없이 표기함
                                • f(n) = 2n^2^ - 7n + 4라면 f(n)의 O-표기는 O(n^2^)
                                • 실행시간이 입력시가 n일 경우 n^2^에 비례하는 알고리즘을 의미함
                                • 가장 자주 사용됨
                                • 상수시간, 로그 시간, 선형 시간, 로그 선형 시간, 제곱시간, 세제곱시간 등이 있음

                              1. Ω(Big-Omega) 표기

                                • 복잡도의 점근적 하한( 즉 효율이 최고로 좋은 상황일 때의 표기)
                                • 위와 동(최소한 이만한 시간은 걸린다)

                              2. Θ(Theta) 표기

                                • 복잡도의 평균 ( 위 두 표기가 서로 같을 경우에 사용)

                                • 전과 동 ()

                              03 비트연산

                              비트 연산자

                              • 다른 연산자들에 비해 실행 시간이 적게 소요, &, , ^, ~, «, » 등이 있음 (Python 정리 참조)

                              • 연산 속도를 향상 키거나 메모리 절약 가능,
                                ex ) 홀수 짝수 판별로 모듈러 연산 M%2 이나 N &1로 마지막 비트값이 0인지 1인지 검사 가능

                              • 1«n 하면 2^n^의 값을 가지며, 부분집합 등을 구하는 데 사용함

                              • i & (1 « j): 특정 비트값이 1인지 0인지 판별하는데 사용

                                비트 연산 1: 특정 위치의 비트값을 확인하는 수식에 대한 예제

                              def BitPrint(i):
	for j in range(7, -1, -1):
	    print('1' if (i&(1<<j)) else '0', end="")
# print("%d" % ((i<<j)&1), end="")
for i in range(-5, 6):
	print("%2d =" % i, end="")# 십진수 출력
    BitPrint(i)# 이진수 출력
    print()

                              비트 연산 2: 4바이트 크기의 인트형 변수에 저장된 값들을 한 바이트씩 읽어서 비트 형태로 출력하는 예제

                              a = 0x10
x = 0x01020304
print("%d=" % a, end="")
BitPrint(a)
print()

print("%08x= " % x, end="")

for i in range(0, 25, 8):
    BitPrint(x>>i)
    print(end=" ")

                              엔디안(Endianness)

                              • 컴퓨터의 메모리와 같은 1차원의 공간에 여러 개의 연속된 대상을 배열하는 방법을 의미하며 HW 아키텍처마다 다름
                              • 속도 향상을 위해 바이트 단위와 워드 단위를 변환하여 연산할 대 올바로 이해하지 않으면 오류가 발생할 수 있음
                                1) 빅 엔디안(Big-endian) : 보통 큰 단위가 앞에 나옴, 네트워크 프로그래밍 0x1234 = 12 34
                                2) 리틀 엔디안(Litte=endian): 작은 단위가 앞에 나옴, 대다수 PC 0x1234 = 34 12

                                XOR

                                비트 연산 4: 비트 연산자 ^를 두 번 연산하면 처음 값을 반환
                                ```python
                                a = 0x86
                                key = 0xAA
                                print("a ==> ", end="")
                                BitPrint(a)
                                print()
                                print("a^=key ==>", end="")
                                a ^= key
                                BitPrint(a)
                                print()
                                print("a^=key ==>", end="")
                                a ^= key
                                BitPrint(a)
                                print()

                              ### 04 진수

#### 진법 변환

* 문제 해결을 위해서 진수 변환이 필요한 경우
- 2진수, 8진수, 10진수, 16진수 등이 있으며 원하는 타진법의 수로 나눈 뒤, 나머지를 거꾸로 읽어서 만듦

- 타진수를 10진수로 변환은 각 자릿값을 해당 진수의 값을 곱해서 구함
  
#### 음의 정수 표현
* 컴퓨터에서의 음의 정수 표현 방법
- Python 정리의 음의 정수 표현방법 참조
  
### 05 실수
  
#### 2진 실수
* 컴퓨터에서의 실수의 표현 방법
  
  - 각 자리수는 2^-1^.... 2^-n^으로 감소하여 구함
    
#### 부동 소수점 표기법
- 컴퓨터에서 실수를 표현하기 위해 소수점의 위치를 고정시켜 표현하는 방식 6.02 X 10^23^

- 32비트는 단정도 실수, 배정도 실수는 64비트로 저장 Python,C 정리 참조 
  
#### 유효 숫자

- 8비트의 255 가지수의 중간(127)을 0으로 놓고 그 위를 양수, 그 아래를 음수로 표현하는 Excess 표현법을 사용함

- 즉 10진수 값 255(2진수값 11111111)은 실제로 128지수를 의미하며 0(00000000)은 -127을 의미

- 컴퓨터는 실수를 근사적으로 표현하므로 작은 오차가 생기게 됨
  
## 02 완전검색
  
### 1. 완전 검색 기법

- 문제의 해를 얻기 위해 가능한 모든 경우들을 나열해 보고 확인하는 기법

- 고지식한 방법(Brute-force), 생성 및 테스트 라고도 불리우며

- 문제 해결하기 위한 간단하고 쉬운 접근법으로, 빠른 시간 안에 문제 해결(알고리즘 설계) 가능

- 대부분의 문제에 적용 가능, 문제의 자료의 크기가 작을 경우 유용
  
#### 고지식한 검색( 순차 검색, Sequential Search)

- 자료들의 리스트에서 키 값을 찾기 위해 첫 번째 자료부터 비교하면서 진행
  
  > 예시 코드
  
```python
def sequentialSearch(a, n, key):
    i = 0
    while i < n and a[i] != key :
        i = i + 1
    if i < n : return i# 성공
    else: return -1# 실패
                              • 리스트의 키값이 존재하지 않을 시, 모든 자료들에 대해 비교 작업이 진행되므로 가장 느림

                              완전 검색으로 시작하기

                              • 문제 해결을 위한 가장 단순한 방법이기 때문에 문제의 크기가 커지면 시간 복잡도가 매우 크게 증가

                              • 모든 경우의 수를 생성하고 테스트하기 때문에 수행 속도는 느리지만, 해답을 찾아내지 못할 확률이 적음

                                • 완전검색을 통해 입력의 크기를 작게 해서 빠르게 답을 구하는 알고리즘 설계

                              • 그리디 기법이나 동적 계획법을 이용해서 효율적인 알고리즘 찾음

                              • 학술적 또는 교육적 목적을 위해 알고리즘의 효율성을 판단하기 위한 척도로 사용

                              • 검정 등에서 주어진 문제를 풀 경우, 완전 검색으로 시작하여 답을 구한 후, 성능 개선을 위해 다른 알고리즘을 사용하는 방식으로 이용함

                              2. 조합적 문제

                              1) 완전 검색과 조합적 문제

                              • 많은 종류의 문제들이 특정 조건을 만족하는 경우나 요소를 찾는 검색

                              • 순열, 조합, 부분집합 같은 조합적 문제들과 관련됨, 조합적 문제에 대한 고지식한 방법

                              2) 순열

                              • 서로 다른 것들 중 몇 개를 뽑아 한 줄로 나열하는것, 서로 다른 n개 중 r개를 택하는 순열 표현

                              • nPr = n!, n Factorial이라고도 부름

                              • 다수의 알고리즘 문제들이 순서화된 요소들의 집합에서 최선의 방법을 찾는 것과 관련됨

                              • N의 크기가 증가할 수록 실행 시간이 기하 급수적으로 증가함, 완전 검색은 비현실적인 방법

                              단순한게 순열을 생성하는 방법

                              {1, 2, 3}을 포함하는 모든 순열을 생성하는 함수

                              for i1 in range(1, 4):
    for i2 in range(1, 4):
        if i2 != i1:
            for i3 in range(1, 4):
                if i3 != i1 and i3 != i2:
                    print(i1, i2, i3)
                              • 일일이 포문을 생성하기 힘듬
                                1. 사전식 순서(Lexicographic-Order)
                                • 요소들이 오름차순으로 나열된 형태가 시작하는 하나의 순열

                              1. 최소 변경을 통한 방법(Minimum-exchange requirement)

                                • 각각의 순열들은 이전의 상태에서 단지 두 개의 요소들 교환을 통해 생성

                                • {1, 2, 3,} 순열에서 1과 3을 교환해서 {3, 2, 1} 순열을 만듦

                                • Johnson-Trotter 알고리즘

                                • N이 1~4이고, 서로 바꾸는 순서를 명시할 때,

                                • (1,2) (2,3), (3,4) (1,2) (3,4) (2,3) (1,2) (3,4) 무한 반복 하면 언젠가는 1,2,4,3으로 끝나 생성

                                • 두 원소의 교환을 통해 생성, 트리 구조를 가짐, 재귀호출로 순열 생성 가능

                              재귀 호출을 통한 순열 생성

                              # a[]: 데이터가 저장된 리스트
# n: 원소의 개수, k: 현재까지 선택된 원소의 수
def perm(n,k) :
	if k == n:# 하나의 순열이 생성됨.
	    print(a)# 원하는 작업 수행
    else:
	    for i in range(k, n):
	        a[k], a[i] = a[i], a[k]# 교환을 통한 선택
            perm(n, k + 1)# 재귀 호출
            a[k], a[i] = a[i], a[k]# 이전 상태로 복귀

                              • 파이선의 라이브러리 itertools의 permutations를 통하여 순열 생성 가능

                              • permutations(list, r) : list에 원소들의 리스트를, r에 원하는 집합의 크기, 생략시 list와 동 크기

                              • repeat=숫자를 적으면 그 수만큼 중복을 허용함 기본값은 1

                              3. 부분집합

                              • 집합에 포함된 원소들을 선택하는 것

                              • 다수의 중요 알고리즘들이 원소들의 그룹에서 최적의 부분 집합을 찾는 것

                              • N 개의 원소를 포함한 집합은 2^n^개가 존재함

                                단순하게 모든 부분 집합 생성하는 방법 ( 4개 원소의 Power set)

                              arr = [2, 3, 4, 5]# 실제 집합
bit = [0]*len(arr)
for i in range(2):
    bit[0] = i# 0번째 원소
    for j in range(2):
        bit[1] = j# 1번째 원소
        for k in range(2):
            bit[2] = k# 2번째 원소
            for l in range(2):
                bit[3] = l# 3번째 원소
                print([arr[x] for x in range(len(bit)) if bit[x]])# 생성된 부분집합 출력
                              • 이런식으로 일일이 for문을 쓰지 않고 비트연산이나 재귀로 생성 가능

                              바이너리 카운팅을 통한 사전적 순서

                              • 부분집합을 생성하기 위한 가장 자연스럽고 간단한 방법

                              • 바이너리 카운팅(Binary Counting)은 사전적 순서로 생성하기 위한 가장 간단한 방법

                              • 원소 수에 해당하는 N개의 비트 열을 이용, i 번째 비트 값이 1이면 i 번째 원소가 포함됬음

                                바이너리 카운팅을 통한 부분집합 생성 코드

                              arr = [2, 3, 4, 5]
n = len(arr)# n: 원소의 개수


for i in range(1<<n):# 1<<n: 부분집합의 개수
    for j in range(n):# 원소의 수만큼 비트를 비교함
        if i & (1<<j):# i의 j번째 비트가 1이면 j번재 원소 출력
            print(arr[j], end=",")
    print()
#또는

for i in range(1<<len(arr)):# 1<<n: 부분집합의 개수
    print([arr[j] for j in range(len(arr)) if i & (i << j)])

                              4. 조합(Combination)

                              • 서로 다른 n개의 원소 중 r개를 순서없이 골라낸 것
                              • nCr = n! / ((n-r)! r!) 로 표현, nCr = n-1Cr-1 + n-1Cr nC0 = 1, nCn = 1 (재귀적 표현)

                                재귀 호출을 이용한 조합 생성 알고리즘
                                ```python

                                listnum: 집합의 크기

                                combinum: 조합 대상의 크기

                              def comb(listtarget, combitarget):
                              global combi
                              global eles
                              global result
                              global cnt

                              cnt += 1
if combitarget == 0:# 만약 모든 원소가 채워지면
    result.append(list(combi))# 완성된것임
elif listtarget < combitarget:# 넣을 수 있는 원소의 수보다 넣어야 하는 조합의 크기가 더 크면 안됨, 2번째 루트가 원소수는 줄이는데 조합수는 줄이지 않으므로 꼭필요함,
    return
else:
    combi[combitarget-1] = eles[listtarget-1]# 해당 조합 자리에 해당 원소를 집어 넣음
    comb(listtarget-1, combitarget-1)# 그 다음 원소를 그 다음번 조합 자리에 넣는 방향
    comb(listtarget-1, combitarget)# 현제 그 자리에 그 원소 대신 다른 원소를 넣는 방향, 2번째 루트 # 선택 정렬과 비슷한 방식이네 eles = [1, 2, 3, 4] result = [] cnt = 0 for i in range(4+1):
combi = [None for _ in range(i)]
comb(4, i) print(result) print(cnt)

                              - 파이썬에서 itertools 라이브러리 객체의 combinations()를 통하여 조합 생성 가능

- cominations_with_replacement()를 통하여 중복 조합 생성 또한 가능
  
## 03 탐욕 알고리즘
  
### 01 탐욕 알고리즘

- 최적해를 구하는 데 사용되는 근시안적인 알고리즘 주로 최적(최대, 최소)값을 구할 때에 쓰임

- 여러 해가 있을 수도 있고 일반적으로 머리 속에 떠오르는 생각을 그대로 쓰면 나타남

- 1) 여러 경우 중 하나 선택, 2) 선택 마다 최적이라고 생각되는 것을 선택, 3) 최종적인 해답에 도달

- 한번 선택된 것은 번복되지 않으므로, 단순하며, 제한적인 문제들에 적용, 지역적으로만 최적
  
#### 1. 동작 과정 (동전 거스름돈 문제 예시)
* 동전 거스름돈 문제
- 거스름돈으로 거내주어야할 동전의 수를 최소화하기 문제
1. 해 선택
   
   - 현재 상태에서 부분 문제의 최적해를 구한 뒤, 부분해 집합에 추가
   - 하나의 선택이 이루어지면 새로운 부분 문제 발생
   - 현재 고를 수 있는 가장 단위가 큰 동전을 골라 거스름돈에 추가

2. 실행 가능성 검사 실시
   
   - 새로운 부분 해 집합의 실행가능 여부 확인
   - 문제의 제약 조건 위반을 검사
   - 거스름 돈이 손님에게 내드려야 할 액수를 초과하는지 확인, 초과하면 1로 돌아가 한 단계 작은 단위의 동전을 추가하여 반복

3. 해 검사
   
   - 새로운 부분 해 집합이 문제의 해가 되는지 확인
   - 전체 문제의 해가 완성되지 않았다면 1의 해 선택부터 다시 시작
   - 손님에게 드려야 하는 거스름돈의 액수와 같은지 확인, 액수가 모자라면 1. 해 선택부터 다시
- 반드시 최적해를 구한다는 보장할 수 없다. 알고리즘의 정확성을 증명하는 과정 필요

- DP(동적 프로그래밍)이나 완전 검색 기법으로 풀어야 한다.

- 무게와 가치를 고려하여 정해진 무게만큼 담는 배낭 문제 (0-1 Knapsack)  등도 비슷하게 푼다.

- 활동 선택 문제(회의시간이 겹치는 회의들을 가능한 많이 회의실에 배정)와 fractional Knapsack(물건을 나눌 수 있는 배낭 문제),Baby-gin 문제(run : 같은 카드 3장, triplet : 연속된 3숫자를 이루는 카드를 가지고 있는가?) 등은 탐욕 기법으로 구해도 해를 구해짐
  
#### 2. 탐욕 기법 검증
1) 탐욕적 선택 속성(Greedy choice property)
- 탐욕적 선택은 최적해로 갈 수 있음, 즉 항상 그 선택은 최적해로 가는 안전한 길임
2) 최적 부분 구조(Optimal substructure property)
- 최적화 문제를 정형화, 하나의 선택을 하면 풀어야 할 하나의 하위 문제가 남음

- [원 문제의 최적해 = 탐욕적 선택 + 하위 문제의 최적해] 임을 증명
  
  > 탐욕 알고리즘이 최적해를 구한다는 것에 대한 증명, 활동 선택 문제 예시
  
1. 문제에서 종료시간이 가장 빠른 활동 am을 선택하는 것은 항상 안전한가?
- 전체 회의들의 집합 S에서 서로 겹치지 않는 최대 크기의 부분 집합 A가 있음(최적해?)

- ak는 A에 속한 종료 시간이 가장 빠른 회의

- 만약 ak = am이면 최대 크기 부분집합에 포함

- 만약 ak != am이면 A에서 ak를 제거하고 am을 추가해도 A 부분집합의 다른 회의와 겹치지 않게 됨,

- 그러므로 종료 시간이 가장 빠른 활동을 선택하는 것은 항상 안전
2. 활동 선택 문제의 해 = 탐욕적 선택 + 하위 문제의 최적해
- S에서 am을 선택하면 하위 문제 S(i~m)와 S(m~j) 존재

- S(i~m)은 공집합이므로 am을 선택한다는 것은 부분 문제 S(m~j)만이 고려해야할 활동들이 존재하는 유일한 부분 문제임을 보임(am이 가장 빠르므로 S(m~j)는 회의가 없다)

- S(m~j)에 회의가 있다면 이는 am 보다 빠르므로 am이 가장 빠른 회의라는 선택에 모순

- 그러므로 S(m~j)는 공집합이다.
  

#### 3. 탐욕 기법과 동적 계획법의 비교
> 비교표

| 탐욕기법                                      | 동적 계획법                           |
| ----------------------------------------- | -------------------------------- |
| 매 단계에서, 가장 좋아 보이는 것을 빠르게 선택한다. (지역 최적 선택) | 매 단계의 선택은 해결한 하위 문제의 해를 기반으로 한다. |
| 하위 문제를 풀기 전에 탐욕적 선택이 먼저 이루어짐              | 하위 문제가 우선 해결 됨                   |
| Top-down 방식                               | Bottom-up 방식                     |
| 일반적으로, 빠르고 간결하다.                          | 좀더 느리고, 복잡하다.                    |

#### 04 Baby-Gin 다시 보기

1. 6개의 숫자는 6자리의 정수 값으로 입력 되며 카운트 리스트에 저장
   - 카운트 리스트는 0에서 9까지의 숫자의 빈도수를 저장하는 리스트
2. Counts 리스트의 각 원소를 체크하여 Run과 Triplet 및 Baby-Gin 여부 판단
   - Counts 리스트의 모든 원소를 1씩 뺀 후에도 Counts의 값이 3 이상이면 Run
   - Triplet은 한 리스트에 숫자가 3개 연속으로 0이 아니면 Triplet
3. 탐욕 알고리즘 방법 적용
   - 카운트 리스트에서 Run과 Triplet 중에 가능한 것을 조사
   - 조사에 사용한 데이터는 삭제
   - 남은 데이터를 다시 Run과 Triplet 중에 가능한 가를 조사

> 대표적인 탐욕 기법의 알고리즘들

| 알고리즘           | 목적                               | 설명                                                   |     |
| -------------- | -------------------------------- | ---------------------------------------------------- | --- |
| Prim           | N개의 정점으로 구성된                     | 정점을 하나씩 선택하는 과정에서 트리를 확장하면서 MST를 찾음                  | 그래프 |
| Kruskal        | 최소 신장트리(MST)를 찾음                 | 싸이클이 없는 서프 그래프들을 확장하면서 MST를 찾음                       | 그래프 |
| Dijkstra       | 주어진 정점에서 다른 정점들에 대한 최단 경로를 찾음    | 주어진 정점에서 가장 가까운 정점을 선택하면서 출발점에서 다른 모든 정점들의 최단 경로를 찾음 | 그래프 |
| Huffman coding | 문서의 압축을 위해 문자들의 빈도수에 따라 코드 값을 부여 | 출현 빈도가 낮은 문자부터 선택해 이진 트리를 완성하고 코드값을 부여함              | 문자열 |

## 04 분할 정복

### 1. 소개, 설계 전략

- Topdown 방식, 작은 부분 부터 구한 뒤 큰 부분을 구하는 방법 ex) 거듭제곱 알고리즘 
1. 분할(Divde) : 해결할 문제를 여러 개의 작은 부분 문제들로 분할

2. 정복(Conquer) : 나눈 작은 문제를 각각 해결

3. 통합(Combine) : 필요 시 해결된 해답을 모음
   
   > 분할 정복 기반 거듭제곱 함수
   
```python
def Recursive_Power(C, n):
    if n == 1:
        return C
    if n % 2 == 0:# even
        y = Recursive_Power(C, n/2)
        return y*y
    else:# odd
        y = Recursive_Power(C, (n-1)/2)
        return y*y*C
                              • n번 곱하는 방식은 O(n) 인 시간 복잡도를 O(log2n)으로 줄일 수 있음

                              2. 병합 정렬

                              1. 소개

                              • 병합정렬은 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식

                              • 분할 정복 알고리즘을 활용하여 자료를 최소 단위의 문제까지 나눈 후, 차례대로 정렬하여 최종 결과 획득, Top-Down 방식 O(n log n)

                              2. 병합 정렬 과정

                              1. 먼저 분할 단계에서 전체 자료 집합에 대하여 최소 크기의 부분 집합이 될 때 까지 계속 분할

                              2. 병합 단계에서 2개의 부분 집합을 정렬하면서 하나의 집합으로 병합 (이 과정에서 1개의 원소 끼리 크기 비교 하여 정렬한다.)

                                알고리즘 : 분할 과정

                              def merge_sort(m):
    if len(m) <= 1:# 사이즈가 0이거나 1인 경우, 바로 리턴
        return m
# 1. Divide 부분
    mid = len(m)//2
    left = m[:mid]
    right = m[mid:]
   
# 리스트의 크기가 1이 될 때까지 merge_sort 재귀 호출
    left = merge_sort(left)
    right = merge_sort(right)
   
# 2. CONQUER 부분: 분할된 리스트들 병합
    return merge(left, right)

                              알고리즘 : 병합 과정

                              def merge(left, right):
    result = []# 두 개의 분할된 리스트를 병합하여 result를 만듦
   
    while len(left) > 0 and len(right) > 0 :# 양쪽 리스트에 원소가 남아있는 경우, 두 서브 리스트의 첫 원소들을 비교하여 작은 것부터 result에 추가함
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    if len(left) > 0 :# 왼쪽 리스트에 원소가 남아있는 경우
        result.extend(left)
    if len(right) > 0 :# 오른쪽 리스트에 원소가 남아있는 경우
        result.extend(right)
    return result
                              • 리스트 사용시 분리, 병합 과정에서 자료의 비교연산과 이동 연산이 발생하여 비효율 적이므로 링크드 리스트를 사용하거나 미리 크기가 정해진 result 리스트에 append, pop 대신 조회 후 값을 대입하는 방법으로 하자

                              3. 퀵 정렬

                              퀵 정렬이란?

                              • 주어진 리스트를 두 개로 분할하고 각각을 정렬, 병합정렬과 비슷해보이나 차이가 있음

                                • 병합 정렬과 달리 기준 피봇을 중심으로 이보다 작은 것은 왼편 큰 것은 오른편에 위치시킴

                                • 병합정렬은 다시 합병하는 후처리 작업이 필요하지만 퀵정렬은 아니다.

                              퀵 정렬 알고리즘

                              동작 과정과 예시 코드

                              # A: 리스트, l: 시작 인덱스, r: 끝 인덱스
# 작은 것부터 큰것 순으로 정렬
def quickSort(A, l, r):
	if l < r:# 시작 인덱스는 끝 인덱스보다 작아야함
	    s = partition(A, l, r)# 피봇을 반환
	    quickSort(A, l, s-1)#왼쪽 부분 재귀 호출
	    quickSort(A, s+1, r)# 오른쪽 부분 재귀 호출

                              Hoare 파티션 알고리즘 아이디어

                              1. P(피봇)값들 보다 큰 값은 오른쪽, 작은 값들은 왼쪽 집합에 위치시킴

                              2. 이동 후, 피봇을 두 집합의 가운데에 위치시킴(피봇을 정렬 상태일 시, 자기가 있어야할 위치로)

                              3. 피봇 값은 다음 정렬 과정에서 제외

                              Hoare-Partition 알고리즘

                              def partition(A, l, r):
    p = A[l]# p: 피봇 값
    i = l + 1# 첫번째 값은 피봇으로 사용함
    j = r
    while i <= j:
        while(i <= j and A[i] <= p) : i += 1
        while(i <= j and A[j] >= p) : j -= 1
        if i <= j:
            A[i], A[j] = A[j], A[i]
    A[l], A[j] = A[j], A[l]
    return j
                              • 피봇 선택 시 왼쪽 끝, 오른쪽 끝, 임의의 세개 값 중에 중간 값을 고르면 좋다. 피봇 값에 따라 효율이 떨어질 수도 있기 때문에

                              Lomuto 파티션

                              • 로무토 파티션은 위와 달리 i, j 두개의 변수가 모두 증가하면서 작업을 수행하게 됨.

                              • 위 보다 속도는 같지만, 더 간단히 구현 가능

                                Lomuto 파티션 알고리즘

                              def partition(A, l, r):
    x = A[r]# 오른쪽 끝값이 피봇
    i = l - 1# 시작위치 -1, i의 인덱스
    for j in range(l, r):# 이 루프를 통해서 i번째까지 피봇보다 크기순서 상관 없이 작은 값들이 모이게 됨(당연히 i+2부터는 피봇보다 순서와 관계없이 큰 값임)
        if A[j] <= x :# == if A[j] <= A[r] : 
            i += 1
            A[i], A[j] = A[j], A[i]
    A[i+1], A[r] = A[r], A[i+1]
    return i+1

                              이진 검색

                              • 자료의 가운데에 있는 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고, 검색을 계속 진행하는 방법

                              • 목적 키를 찾을 때까지 이진 검색을 순환적으로 반복 수행해 검색 범위를 반으로 줄여가면서 보다 빠르게 검색 수행.

                              • 단 자료가 미리 정렬된 상태여야 함, 순차검색 보다 효율적임.

                              이진 검색의 검색 과정

                              1. 자료의 중앙에 있는 원소를 고른다.

                              2. 중앙 원의 값과 찾고자 하는 목표 값을 비교한다.

                              3. 목표 값이 중앙 원소의 값보다 작으면 왼쪽 반에 대해서만 새로 검색 크면 반대로 오른쪽 반에서

                              4. 찾고자 하는 값을 찾을 때 까지 반복

                              알고리즘 :반복 구조

                              • 자료 삽입, 삭제 발생 시, 리스트의 상태를 항상 정렬 상태로 유지하는 추가 작업 필요

                                이진 검색 알고리즘

                              # a : 검색할 리스트
# key : 검색하고자 하는 값
def binarySearch(a, key):
    start = 0
    end = len(a) - 1
    while start <= end:
        middle = start + (end - start) // 2
        if key == a[middle]:# 검색 성공
            return middle
        elif key < a[middle]:
            end = middle - 1
        else :# a[middle] < key :
            start = middle + 1
    return -1# 검색 실패

                              재귀 구조 이진 검색

                              # a : 검색할 리스트
# key : 검색하고자 하는 값
def binarySearch2(a, low, high, key):
    if low > high :# 검색 실패
        return -1# 검색 실패 False
    else:
        middle = (low + high) // 2
        if key == a[middle]:# 검색 성공
            return middle# True
        elif key < a[middle]:
            return binarySearch2(a, low, middle-1, key)
        else:# a[middle] < key:
            return binarySearch2(a, middle+1, hight, key)

                              분할 정복 사례

                              • 병합 정렬 : 외부 정렬의 기본이 되는 정렬 알고리즘

                                • 멀티코어 CPU, 다수의 프로세서에서 정렬 알고리즘 병렬화를 위해 병합 정렬 알고리즘 활용

                              • 퀵 정렬 : 매우 큰 입력 데이터에 대해서 좋은 성능을 보이는 알고리즘

                                • 생물 정보 공학 등에서 특정 유전자 찾는데 사용, 문자열에서도 접이어 배열 학습

                              • 최근접 점의 쌍 문제 : 2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한쌍의 점을 찾는 문제

                                • 컴퓨터 그래픽스, 컴퓨터 비전, 지리 정보 시스템, 항공 그래픽 제어, 마케팅 등에 사용

                              05 백트래킹

                              1. 백트래킹

                              소개

                              • N-Queen 문제, 순열, 동전 거스름돈 문제 등에 사용됨 (190919 참조)

                              • 해를 찾는 도중에 막히면(즉 해가 아니면) 되돌아가서 다시 해를 찾아가는 기법

                              • 최적화 문제와 결정 문제를 해결 할 수 있다.

                                • 문제의 조건을 만족하는 해가 존재하는지의 여부를 yes 또는 no로 답하는 문제

                              • 초기 상태에서 목표 상태로 가는 경로를 탐색하는 기법

                                • 여러가지 선택지(옵션)들이 존재하는 상황에서 한가지 선택
                                • 선택이 이루어지면 새로운 선택지들의 집합 생성
                                • 선택을 반복하면 최종 상태에 도달

                              • 보통 재귀 함수로 구현하며, 반복구조로도 구현 가능하나 재귀 함수가 백트래킹하기에 더 쉽다.

                              상태 공간 트리

                              • 해를 찾기 위한 선택의 과정을 트리로 표현

                              • 트리의 내부 노드는 최종 상태로 가는 중간 상태를 나타냄

                              • 트리의 단말 노드는 하나의 후보해에 대한 최종 상태가 됨

                                • 후보해 : 루트 노드에서 단말 노드로 가는 경로,

                              • 상태 공간 트리를 탐색하는 것은 모든 후보해들을 탐색하는 것

                              • 트리를 깊이 우선 탐색 하는 방법이 백트래킹 알고리즘의 기본 형태

                              백트래킹과 깊이 우선 탐색과의 차이

                              • 백트래킹 기법은 어떤 노드에서 출발한 경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음으로써 시도의 횟수를 줄임( Prunning 가지치기)

                              • 깊이 우선 탐색은 그러하지 않으므로 경우의 수가 너무 많아 처리가 불가능

                              • 백트래킹 또한 최악의 경우 깊이 우선 탐색과 같을 수 있음

                              • 즉 백트래킹은 모든 후보해를 검사하지 않고 유망하지 않다(해답이 될 수 없다)고 결정되면 노드의 부모로 돌아가 다음 자식 노드로 감,
                                -예를 들어 N-Queen 문제에서 1번째 퀸과 2번째 퀸이 서로 경로상에 존재하면 3번째 퀸은 그냥 놓아보지 않고 2번째 퀸을 다른 곳에 다시 놓는다.

                              • 트리에 관한 이야기는 알고리즘 기초 참조

                                N-Queen 슈도 코드

                              f(i, N)
    if i==N# 모든 줄에 퀸을 놓으면
        cnt += 1
    else
        for j : 0 -> N-1
            if col[j] == 0 and right[i+j]==0 and left[i-j+N-1]==0# 다른 줄에 j번 열에 퀸이 없어야 하고
	    # 왼쪽 대각선과 오른쪽 대각선에 퀸이 없어야 한다.
                board[i][j] = 1
                col[j] = 1# 현재 줄에서 j열을 사용함으로 표시
                right[i+j] = 1
                left[i-j+N-1] = 1
                f(i+1, N)# j열에 놓을 수 있으면 다음 줄로 이동
                col[j] = 0
                right[i+j] = 0
                left[i-j+N-1] = 0

                              백트래킹을 이용한 알고리즘의 진행 절차

                              1. 상태 공간 트리에 대한 깊이 우선 탐색 실시

                              2. 방문하는 노드가 유망한지 여부 점검

                                • 노드의 유망성 판단 방법은 해를 찾으려는 문제에 따라 달라짐

                              3. 만일 선택한 노드가 유망하지 않을 경우, 해당 노드의 부모 노드로 돌아가서 검색 계속 진행

                                일반적인 백트래킹 알고리즘 코드

                              def checknode(v):# node
	if promising(v): 
        if there is a solution at v:
            write the solution
        else:
            for u in each child of v:
            checknode(u)

                              power set 생성 방법

                              • power set이란 어떤 집합의 공집합과 자기 자신을 포함한 모든 부분집합,

                              • 구하고자 하는 어떤 집합의 원소 개수가 n일 경우 부분집합의 개수는 2^n^

                              • algorithmTIL 190919 참조

                              powerset 생성법

                              # listnum: 집합의 크기
# combinum: 조합 대상의 크기
def comb(listtarget, combitarget):
    global combi
    global eles
    global result
    global cnt

    cnt += 1
    if combitarget == 0:# 만약 모든 원소가 채워지면
        result.append(list(combi))# 완성된것임
    elif listtarget < combitarget:# 넣을 수 있는 원소의 수보다 넣어야 하는 조합의 크기가 더 크면 안됨, 2번째 루트가 원소수는 줄이는데 조합수는 줄이지 않으므로 꼭필요함,
        return
    else:
        combi[combitarget-1] = eles[listtarget-1]# 해당 조합 자리에 해당 원소를 집어 넣음
        comb(listtarget-1, combitarget-1)# 그 다음 원소를 그 다음번 조합 자리에 넣는 방향
        comb(listtarget-1, combitarget)# 현제 그 자리에 그 원소 대신 다른 원소를 넣는 방향, 2번째 루트

# 선택 정렬과 비슷한 방식이네

	eles = [1, 2, 3, 4]
	result = []
	cnt = 0
	for i in range(4+1):
	    combi = [None for _ in range(i)]
	    comb(4, i)
	print(result)
	print(cnt)

                              순열 생성 알고리즘과 슈도 코드

                              슈도 코드
                              ```python

                              order[] : 순열의 순서를 저장하는 리스트

                              def permutation(order, k, n):
                              if k == n:
                              print_order_array(order, n)
                              else:
                              check = [False] * n
                              for i in range(k):
                              check[order[i]] = True
                              for i in range(n):
                              if check[i] == False:
                              order[k] = i
                              permutation(order, k+1, n)

                              > python 순열 알고리즘

```python
def f(n, path, used):
    global pathes
    for k in range(idx):
        if used[k] == 0:
            used[k] = 1
            path[n] = locates[k]
            if n == idx-1:
                print(path)
            f(n+1, path, used)
            used[k] = 0

idx = 5
locates = [i for i in range(idx)]
visited = [0 for j in range(idx)]
soonyeal = [0 for j in range(idx)]
f(0, soonyeal, visited)

                              06 그래프의 기본과 탐색

                              그래프 기본

                              소개

                              • 그래프란 : 객체( 사물 또는 추상적 개념)들과 객체들 사이의 연결 관계 표현

                              • 정점(Vertex)들의 집합과 정점을 연결하는 간선(Edge)들의 집합으로 구성된 자료 구조
                                정점 : 각 객체의 표현, 간선 : 이들 사이의 관계

                              • 선형 자료구조나 트리 자료구조로 표현 어려운 N:N 관계를 가지는 원소들을 표현하기에 용이

                              • 인접행렬은 만들기 쉽고 직관적이나 쓸데없는 메모리와 효율 낭비가 심함

                                1. 무향 그래프(Undirected Graph) : 서로 대칭적인 관계를 연결해서 나타낸 그래프

                              1. 유향 그래프(Directed Graph): 간선을 화살표로 표현하고 방향성의 개념(서로 대칭적 아님)

                              2. 가중치 그래프(Weighted Graph): 각 간선간에 비용이 있음, 이동 소요 시간, 비용 등
                                *인접(Adjacency) : 두 개의 정점이 간선에 의해 연결해 있는 경우

                                • 완전 그래프에 속한 임의의 두 정점들은 모두 인접해 있음,
                                • 부분 그래프 : 완전 그래프에서 일부의 정점이나 간선을 제외한 그래프
                                  * 경로: 간선들을 순서대로 나열한 것, 단순경로는 경로 중 한 정점을 최대한 한번만 지나는 경로

                              • 사이클: 시작한 정점에서 끝나는 경로 (ex) 1 - 3 - 5 - 1)

                              • 0 - 2 - 4 - 6 (경로)

                              • 사이클이 없는 유향 그래프 (DAG, Directed Acyclic Graph)

                              그래프 표현

                              • 간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
                                1. 인접 행렬(Adjacent matrix) : 정점수 * 정점수 크기의 2차원 리스트를 이용해 간선 정보 저장
                                • 두 정점을 연결하는 간선의 유무를 행렬 형태로 표현
                                • 행 번호와 열 번호는 그래프의 정점에 대응, 두 정점이 인접되있으면 1 아니면 0
                                • 무향 그래프는 i번째 행의 합과 열의 합이 같으며 해당 정점의 차수(연결된 간선수)이다.
                                • 유향 그래프는 행의 합(가로줄)은 진출 차수(나가는 간선), 열의 합은 진입 차수(반대)이다.
                                • 인접행렬의 단점 :
                                  1) 행과 열이 같은 부분은 자기 자신으로 가는 간선을 의미하므로 0으로 놓게 되고 쓸데 없는 메모리 낭비가 된다.
                                  2) 정점의 개수 n이 커지면 인접 행렬에 필요한 메모리 크기는 n^2^에 비례해서 커진다.
                                  3) 어떤 정점의 인접 정점을 찾을 때 마다, 천 개의 슬롯을 조사해야 함
                                • 그래프에 포함된 간선의 수가 많지 않은 경우 메모리 사용을 줄이기 위해 간선들의 정보를 나열해서 저장하는 것이 나음
                                  • 간선 리스트에서 어떤 정점의 인접 정점은 일치하는 시작 정점을 찾으면 됨
                              1. 인접 리스트(Adjacent List) : 각 정점마다 인접 정점으로 나가는 간선의 정보 저장
                                • 정점의 개수에 비해 상대적으로 간선의 수가 적을 때, 간선들을 리스트에 연속으로 저장해 사용

                              • 인접리스트는 구현이 힘듬 대신 메모리와 효율 이 괜찮음 10000개 이상의 정점이 있을시 쓸것,

                              • 각 정점에 대한 인접 정점들을 순차적으로 표현

                              • 정점의 개수만큼 메모리 주소를 저장하는 리스트 존재,

                              • 정점의 번호에 대응하는 곳은 연결 리스트의 첫번째 노드에 대한 주소 저장

                              • 각 정점의 연결 리스트는 인접 정점의 개수만큼 노드를 연결

                              그래프 탐색

                              그래프 순회

                              • 비선형 구조인 그래프로 구현된 모든 자료(정점)을 빠짐없이 탐색, 그래프 탐색의 대표적인 방법

                              1) 시작 정점에 갈 수 있는 한 방향을 선택해서 다음 정점으로 이동

                              2) 선택된 정점에서 다시 1)과 같은 작업을 반복 수행하면서 갈 수 있는 경로가 있는 곳까지 깊이 탐색, 이때 이미 방문했던 정점은 재방문하지 않음

                              3) 더 이상 갈곳이 없으면, 가장 최근에 방문한 갈림길이 있는 정점으로 되돌아와서 다른 방향의 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회 방법

                              • 가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탐색 반복

                              • 후입선출 구조의 스택 사용하거나 재귀 호출을 이용해서 구현

                                DFS 알고리즘 - 재귀

                              # G: 그래프, v: 시작 정점
# visited: 정점의 방문 정보 표시, False로 초기화
# G[v]: 그래프 G에서 v의 인접 정점 리스트

def DFS_Recursive(G,v):
    visited[v] = True
    visit(v)
    for w in G[v]:
        if not visited[w]:
            DFS_Recursive(G,w)

                              DFS 알고리즘 - 반복

                              # G: 그래프, S: 스택, v: 시작 정점
# visited: 정점의 방문 정보 표시, False로 초기화
# G[v] : 그래프 G에서의 v의 인접 정점 집합
def DFS_Iterative(S, v):
    S = [v]
	while stack:
	    v = S.pop()
	    if v not in visited:
	        visited.append(v)
		    visit()
	        S.extend(G[v] - set(visited))
	    return visited

                              -반복 구조 stack DFS 시, push와 함께 visited를 표시하자 그러면 조금 줄일 수 있다.

                              1. 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문

                              2. 방문했던 정점들을 다시 시작점으로 하여 앞의 과정을 반복 수행

                                • 이미 방문한 정점은 재방문하지 않음

                                • 선입 선출 구조인 큐를 활용함

                                  너비우선 탐색 알고리즘 - 재귀

                              # G : 그래프, Q : 큐, v : 시작 정점
# visited: 정점의 방문 정보 표시, False로 초기화
# G[v]: 그래프 G에서의 v의 인접 정점 리스트
def BFS(Q, v):
	Q.append(v)
    visited[v] = True
    visit(v)
    while Q:
	    v = Q.pop(0)
        for w in G[v]:
	        if not visited[w]:
	            Q.append(w)
                visited[w] = True
                visit(w)
# 시장정점에서 거리를 구하는 확장 알고리즘 D[]: 최단 거리, P[]: 최단 경로
def BFS2(Q, v):
	D[v] = 0
    P[v] = v
    Q.append(v)
    visited[v] = True
    visit(v)
    while Q:
	    v = Q.pop(0)
        for w in G[v]:
	        if not visited[w]:
	            Q.append(w)
                visited[w] = True
                visit(w)
                D[w] = D[v] + 1
                P[w] = v
                              • BFS 정점으로 부터의 거리 ,visited 표시할 때, V[i]=1 대신, V[i] = V[n] + 1로 하면 시작점과 해당 정점까지의 거리를 구할 수 있다. 대상 V[대상 노드 인덱스] - 시작점 V[시작점] = 거리, 오직 시작점과의 거리만 구할 수 있음, 0이면 경로가 없는거

                              위상 정렬(Topological Sort)

                              • DAG만 가능(Directed Acyclic Graph) : 방향성 있는 비 사이클 그래프 O(N+M)

                              • 제일 앞에 오는 정점은 Indegreer가 0이여야 한다.

                              • 위상정렬을 한 후 Indegree가 0인 정점은 앞으로 옮겨도 정렬이 유지됨

                              알고리즘

                              Indegree : 이 노드로 들어오는 간선 수, Outdegree: 노드에서 나가는 간선수

                              1. Indegree가 0인 정점들을 큐에 추가한다.
                              2. 큐가 빌 때까지 다음을 반복한다.(O(N))
                                • 1) 큐에서 정점을 하나 뽑아 배치한다.O(1)
                                • 2) 해당 정점에서 뻗어나가는 간선(=이 노드에서 갈 수 있는 다른 노드들로 향하는 간선)들을 삭제한다.(O(M)) (3번도 이때 같이 처리하면 O(N)이 사라짐)
                                • 3) 이로 인해 Indegree가 0이 된 정점들을 큐에 추가한다.(O(N))
                              3. 배치가 안된 정점이 남아있다면, 주어진 그래프에 사이클이 존재하는 것이다.(DAG 아님)
                                • 큐 대신 스택으로 쓰면 정답이지만 경우의 수가 다른 정답을 내놓는다.

                              (위상 정렬은 여러가지 경우의 수의 정답을 가진 경우가 많음).

                              import sys, heapq
input = sys.stdin.readline
studentNum, compNum = map(int, input().split())
indegree = [[] for _ in range(studentNum+1)]
outdegree = [[] for _ in range(studentNum+1)]
for _ in range(compNum):
	fr, bk = map(int,input().split())
    indegree[bk].append(fr)
    outdegree[fr].append(bk)
hq = []
for i in range(1, studentNum+1):
    if len(indegree[i]) == 0:
        hq.append(i)
while hq:
    student = heapq.heappop(hq)
    print(student, end=" ")
    for taller in outdegree[student]:
        indegree[taller].remove(student)
        if len(indegree[taller]) == 0:
            heapq.heappush(hq, taller)

                              상호배타 집합들

                              서로소 또는 상호배타 집합들

                              • 서로 중복 포함된 원소가 없는 집합들로 교집합이 없음,
                              • 집합에 속한 하나의 특정 원소(대표자, Representative)를 통해 각 집합들을 구분
                              • 구현이 간단하고 동작속도가 빠르기 때문에 그래프 영역에서 많이 사용되고 다른 알고리즘의 일부로 활용, ex) 그래프의 연결성 확인하기, KRUSKAL MST 알고리즘 각 집합에 속한 원소 수 관리
                              • 상호배타 집합을 표현하는 방법으로 연결리스트와 트리구조가 있다.
                              • 문제를 풀 때 양반향인지 단방향인지 주의, 시작할 때 p[rep(n2)] = repr(n1) 식으로 사이클을 줄이고 루트 최적화를 할 수 있다.
                              • 배열로 만들수 있지만 배열로 만들면 O(N)으로 느리다
                              • 트리로 만들면 좀더 빠르다(다만 집합의 부모를 집합의 대표로 바꿔주는 pathcompression 작업 필수O(n^2)에서 O(nlog*n) 로 바꿔줌)
                              • a(N) = log* n(ackermann 함수) = log n보다 적음, n이 100억이여도 4, 상수시간 수준 보통 5이하임
                              • 상호배타 집합 연산의 종류
                                1. Make-Set(x) - 원소 x 만으로 구성된 집합을 생성하는 연산
                                2. Find-Set(x) - 임의의 원소 x가 속한 집합을 알아내기 위해 사용하며, 집합의 대표자를 알기 위한 연산
                                3. Union(x, y) - x 원소가 속한 집합과 y 원소가 속한 집합을 하나의 집합으로 합치는 연산
                                • 합쳐진 새로운 집합의 대표자는 아무거나 골라도 됨
                                  이외에 Size함수로 합쳐질때마다 size 값이 갱신되도록 하여 전체 노드의 갯수를 알 수 있게 가능
                                  이 를 통하여 가장 큰 집합 추적, 노드 개수가 몇개 이상이 되는 시점을 찾을 수 있음

                              DFS 시 재귀는 백트래킹을 놓기 쉽고 스택을 이용한 반복구조는 빠르다 즉 모든 구조를 돌아야할 때는 반복구조로, 가지치기가 가능하면 재귀구조로 짜는게 빠름( 반복구조는 append와 pop을 쓰지 말고 top포인터로 쓰면 빠르다)

                              연결리스트 표현

                              • 같은 집합의 원소들은 하나의 연결 리스트로 관리

                              • 연결리스트의 첫 번째 원소를 집합의 대표 원소로 선택

                              • 각 원소는 집합의 대표 원소를 가리키는 링크를 가짐

                              • 두 집합을 합칠 때는 크기가 작은 집합을 큰 집합의 뒤에 연결

                              트리 표현

                              • 연결리스트보다 더욱 효율적임

                              • 하나의 집합(a disjoint set)을 하나의 트리로 표현

                              • 자식 노드가 부모 노드를 가리키며 루트 노드가 대표자가 됨

                              • Union 함수 사용시, 해당 루트의 부모를 다른 루트노드로 바꾸면 됨

                              • find-set 시, 자기 자신을 부모로 가리키는 원소를 찾을때 까지 탐색(즉, 루트노드)

                              • 상호 배타 집합을 트리로 표현하기 위해 리스트 사용,

                                • 각 원소의 부모에 대한 정보 저장 형태, 자기 자신을 가리키면 대표자가 됨

                                  트리 표현 시 상호배타 집합 연산들에 대한 알고리즘

                              def Make_Set(x):# 유일한 원소 x를 포함하는 새로운 집합을 생성하는 연산
    p[x] = x    
    
def Find_Set(x):# x를 포함하는 집합을 찾는 연산
    if x == p[x] : return x
    else: return Find_Set(p[x])
    
def Union(x, y):# x와 y를 포함하는 두 집합을 통합하는 연산
    p[Find_Set(y)] = Find_Set(x)

                              • 문제점 : 집합 Union하는 과정에서 편향된 트리 구조 생성, 이로 인해 함수에서 여러 재귀 호출이 필요함, 이를 해결하기 위해 모든 원소들의 부모를 루트 노드로 하면 1번만 호출해도 부모 찾아감

                              • 연산 효율을 높이기 위해

                                1. Rank를 이용한 Union

                                  • 각 노드는 자신을 루트로 하는 Subtree의 높이를 랭크(Rank)라는 이름으로 저장
                                  • 두 집합을 합칠 때 Rank가 낮은 집합을 Rank가 높은 집합에 붙임
                                  • 두 집합의 Rank값이 같으면 랭크값이 1 증가됨

                                2. Path compression

                                  • Find-Set을 행하는 과정에서 만나는 모든 노드들이 직접 Root를 가리키도록 부모 정보를 변경

                                    효율성이 고려된 상호배타 집합 연산들

                              # p[x]: 노드 x의 부모 저장
# rank[x]: 루트 노드가 x인 트리의 랭크 값 저장
# 유일한 멤버 X를 포함하는 새로운 집합을 생성하는 연산
def Make_Set(x):
	p[x] = x# 자기자신
	rank[x] = 0
  
# x를 포함하는 집합을 찾는 오퍼레이션
  
def Find_Set(x):
	if x!= p[x]:# x가 루트가 아닌 경우
	    p[x] = Find_Set(p[x])# Path Compression
    return p[x]
  
# 특정 노드에서 루트까지의 경로에 존재하는 노드가 루트를 부모로 가리키도록 갱신
  
# x와 y를 포함하는 두 집합을 통합하는 오퍼레이션
  
def Union(x, y):
    Link(Find_Set(x), Find_Set(y))
  
def Link(x,y):
    if rank[x]>rank[y]:
        p[y] = x
    else:
        p[x] = y
    if rank[x] == rank[y]:
        rank[y] += 1

                              Indexed Tree(Segment tree)

                              Sum Indexed Tree (도식화)

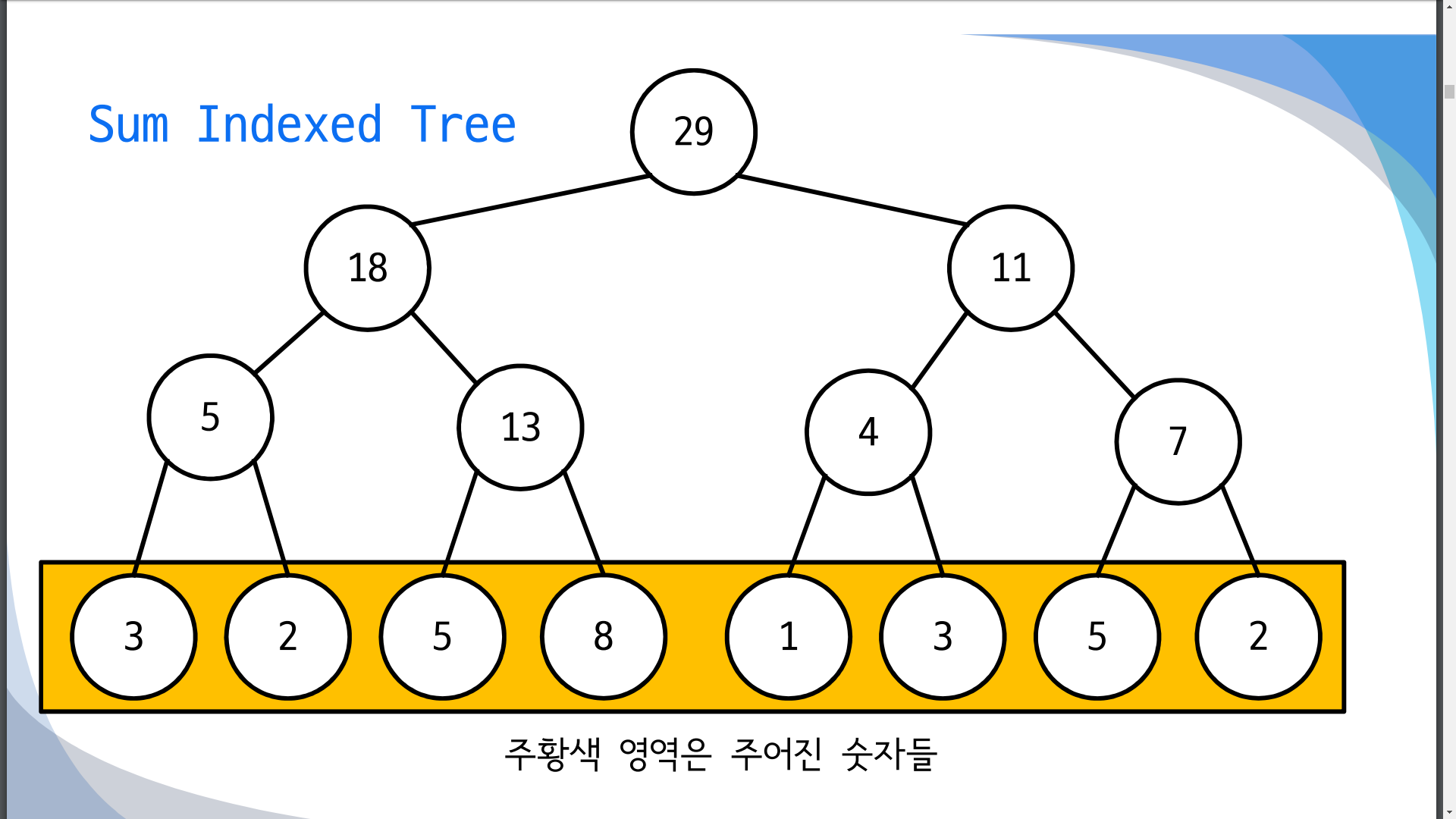
                              • 숫자의 갱신과 주어진 구간([a:b])에 대해서 원하는 연산 (총합, 최대값, 최솟값)을 O(logN)의 시간복잡도로 해결할 수 있는 자료구조, (tree 구조를 기반)

                              • 높이는 log(N)+1, 부모 노드의 값은 두 자식 노드 값의 계산 결과(합이면 두 노드의 합, 최대값이면 둘 중 더욱 큰거)

                              • 자식노드가 바뀌면 부모노드와 조상노드들을 바꿔줘야함, 갱신 시간복잡도: O(logN)

                              • 같은 높이의 3개 이상의 노드가 사용될 일이 없다( 비둘기집의 원리) 연산 시간복잡도 O(logN)

                              • 1차원 배열로 구현 가능, 루트가 인덱스 1부터 시작

                              알고리즘

                              • 1차원 배열의 단말부분에 내가 쓰고 싶은 부분을 넣는다.

                                • 노드 갯수의 4배를 하면 된다.((노드갯수+ 연산을 위한 빈 노드들) + 내부(조상 노드들)갯수 (앞 두 합의 2배) )
                                • 연산을 위해 인덱스를 구하는 방법 : 트리의 단말 노드 갯수 - 1 이 가장 마지막 레벨이 낮고 마지막에 나오는 부모 노드(매직 넘버)이 이후로가 단말노드의 첫번재 인덱스

                              • 그 밑(부모들)에는 두 단말노드의 연산값, 그 부모 노드 둘의 연산값들을 넣는다.( O(N)으로 생성가능)(전체 갯수가 최대 2N개이므로 ( 단말노드 N, 내부노드 N-2~N-2))

                              • 빈 배열에 넣을 값은 용도에 따라 다른데, 예를 들어 합이 목적이면 0을 넣으면 된다. 최솟값이 목적이면 해당 자료형의 최소값(연산에 대한 항등원)을 넣으면 된다.

                              • left와 right 두 포인터를 가지고 left의 인덱스가 홀수면 left++, right 인덱스가 짝수면 right–(둘다 누적 한뒤 실행한다.)

                                • 모든 홀수번 정점은 오른쪽 자식이고, 모든 짝수번 정점은 왼쪽 자식이므로

                                • 이후 left와 right의 부모로 간뒤(나누기2) 이후 누적이나 연산한 후, 무한 반복

                                • 그러다 left가 right 보다 크면 모든 연산이 끝난 것이다.

                              import sys
input = sys.stdin.readline
numCount= int(input())
# segment tree 
nums = [0 for _ in range(numCount*2)] + list(map(int, input().split())) + [0 for _ in range(numCount)] 
for i in range(len(nums), -1, -1):
    if (2*i+1 < len(nums)):
        nums[i] = nums[2*i]+nums[2*i+1]
left, right = map(int, input().split())
left += numCount*2 - 1
right += numCount*2 - 1
result = 0
while(left <= right):
    if (left&1):
        result += nums[left]
        left += 1
    if not (right&1):
        result += nums[right]
        right -= 1        
    left = left//2
    right = right//2
print(result)
# 배열의 값이 바뀌는 경우가 아니면 왠만하면 DP로 푸는게 더빠르고 쉽다.

                              07 그래프의 최소 비용 문제

                              1. 최소 신장 트리

                              • 그래프의 최소 비용 문제는 보통

                                1) 최소 신장 트리 문제

                                • 가중치 그래프에서 모든 정점들을 연결하는 간선들의 가중치의 합이 최소가 되는 트리를 찾는 문제
                                  2) 최단 경로 문제
                                • 시작 정점에서 목표 정점까지 가는 간선의 가중치의 합이 최소가 되는 경로를 찾는 문제

                              최소 신장 트리 소개

                              • 신장 트리(Spanning Tree): n개의 정점을 포함하는 무향 그래프에서 n개의 정점과 n-1개의 간선으로 구성된 트리, 그래프에 존재하는 신장 트리의 수는 정점의 개수와 간선의 수에 비례해 증가

                              • 최소 신장 트리(Minimum Spanning Tree) : 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리

                              2. 프림 알고리즘

                              프림 알고리즘이란?

                              • 한 정점에서 연결된 간선들 중 하나씩 선택하면서 최소 신장 트리를 만들어 가는 방식
                                1) 임의의 정점을 하나 선택해서 시작

                              2) 선택한 정점들과 인접하는 정점들 중에 최소 비용의 간선이 존재하는 정점 선택

                              • heap으로 짜면 빠르다. O(logN)

                              3) 사이클이 있는지 검사 후 없으면 그 정점을 그대로 최소 신장트리에 추가

                              • 검사 방법은 이미 추가 했었는가?(visited) 또는 위상정렬 또는 서로소 집합 부모 확인

                              4) 모든 정점이 선택될 때 까지 두 번째 과정 반복

                              • 정점의 수가 n개라면 n-1개의 간선이 선택되며 하나의 트리를 구성하게 됨
                              프림 알고리즘의 동작
                              1) 트리 정점들(Tree vertices) : 최소 신장 트리를 만들기 위해 선택된 정점들
2) 비트리 정점들(Non-tree vertices) : 선택되지 않은 정점들

                              프림 알고리즘 코드

                              def MST_PRIM(G, s):# G: 그래프, s: 시작 정점
    key = [INF]*N# 1. 가중치를 무한대로 초기화
    pi = [None]*N# 2. 트리에서 연결될 부모 정점 초기화
    visited = [False]*N# 3. 방문 여부 초기화
    key[s] = 0# 4. 시작 정점의 가중치를 0으로 설정

    for _ in range(N):# 5. 정점의 개수만큼 반복
        minIndex = -1
        min = INF
        for i in range(N):# 6. 방문 안한 정점중 최소 가중치 정점 찾기
            if not visited[i] and key[i] < min:
                min = key[i]
                minIndex = i
        visited[minIndex] = True# 7. 최소 가중치 정점 방문처리
        for v, val in G[minIndex]:# 8. 선택 정점의 인접한 정점
            if not visited[v] and val < key[v]:# 9 방문하지 않고 갱신될 수 있는 정
                key[v] = val# 10. 가중치 갱신
                pi[v] = minIndex# 11. 트리에서 연결될 부모 정점

                              3. 크루스칼 알고리즘

                              크루스칼 알고리즘 소개

                              • 사이클이 생기지 않도록 최소 가중치 간선을 하나씩 선택해서 최소 신장 트리를 찾는 알고리즘

                                • N개의 정점을 포함하는 그래프에서 n-1개의 간선을 선택하는 방식

                                • 간선을 선택해 나가는 과정에서 여러 개의 트리들이 존재

                                • 초기 상태는 n개의 정점들이 각각 하나의 트리 ( 상호 배타 집합)이 존재하며

                                • 간선을 선택하면 간선의 두 정점이 속한 트리가 연결되어 하나의 집합으로 변함

                                • 선택한 간선의 두 정점이 이미 연결된 트리에 속한 정점들일 경우 사이클이 생기므로 두 정점에 대해 같은 집합의 원소 여부 검사

                              크루스칼 알고리즘의 동작

                              1. 최초, 모든 간선을 가중치에 따라 오름차순으로 정렬

                              2. 가중치가 가장 낮은 간선부터 선택하면서 트리 증가시킴

                                • 사이클이 존재하면 다음으로 가중치가 낮은 간선 선택

                              3. n-1개의 간선이 선택될 때까지 두 번째 과정을 반복

                                크루스칼 알고리즘의 동작과정

                              def MST_KRUSKA(G):
    mst = []# 1. 최소 거리 간선 집합으로 공집합 생성
   
    for i in range(N):# 2. 각 노드를 집합으로 만들기
        Make_Set(i)
    G.sort(key = lambda t:t[2])# 3. 가중치 기준으로 정렬
   
    mst_cost = 0# 4. MST 가중치
   
    while len(mst) < N-1:# 5. 필요한 간선의 갯수(노드 갯수 - 1)만큼
        u, v, val = G.pop(0)# 6. 최소 가중치 간선 가져오기
        if Find_Set(u) != Find_Set(v):# 7 만약 to node와 from node가 같은 집합에 있지 않다면
            Union(u, v)           # 8 두 노드를 같은 집합으로 합치기
            mst.append((u,v))   # 9 최소 거리 간선 집합에 (u, v) 추가
            mst_cost += val

                              • 간선 선택 과정에서 생성되는 트리를 관리하기 위해 상호 배타 집합 사용

                                • 트리에 속한 노드들은 자신을 루트로 하는 서브트리의 높이를 랭크 이름으로 저장

                              • 선택한 간선으로 두 개의 트리가 한 개의 트리로 합쳐질 때 각 트리에 해당하는 상호 배타 집합을 Union연산으로 합침

                                • 랭크 값이 작은 트리를 랭크 값이 큰 트리의 서브트리로 포함시킬 경우 트리에 포함된 노드들의 랭크 값 수정 불필요

                              4. 최단 경로

                              최단 경로란?

                              • 간선의 가중치가 있는 유향 그래프에서 두 정점 사이의 경로들 중 가중치의 합이 최소인 경로

                              • 엄밀히말하면 한 정점에서 다른 정점들 까지 가는 최소거리이긴 하다.

                                • 단일 시작점 최단 경로 문제

                                  • 출발점에서 다른 모든 정점들에 이르는 최단 경로를 구하는 문제
                                    • 다익스트라(Dijkstra) 알고리즘 : 음의 가중치를 허용하지 않음
                                    • 벨만-포드(Bellman-Ford) 알고리즘 : 음의 가중치 허용, 가중치 합이 음인 사이클은 허용하지 않음

                                • 모든 쌍 최단 경로 문제

                                  • 모든 정점 쌍 간의 최단 경로를 구하는 것으로 플로이드-워샬 알고리즘 이용

                              5. 다익스트라 알고리즘

                              다익스트라 알고리즘이란?

                              • 시작 정점에서 거리가 최소인 정점부터 선택해 나가면서 최단 경로를 구하는 방식

                              • 탐욕 기법을 사용한 알고리즘으로 최소 신장 트리를 구하는 프림 알고리즘과 유사

                              • 시장 정점(r)에서 끝 정점(t)까지의 최단 경로에 정점 x 가 존재,

                              • 최단 경로는 r에서 x까지의 최단 경로와 x에서 t까지의 최단 경로로 구성

                              • 시작점에서의 최단 경로를 찾은 정점들의 집합(S)을 관리

                              • 집합 S에 포함되지 않은 정점들 중에 출발점에 가장 가까운 정점 선택

                              대략적인 알고리즘

                              1) 기본버전 알고리즘

                              1. 시작 노드 주위 이외의 최단거리를 무한대로 놓는다
                                1. 최단 거리가 확정되지 않은 노드(거리가 무한대) 중 Dis[i]값이 가장 작은 노드(v)를 고른다(O(N))
                                2. 그 노드로부터 이어진 간선들을 이용하여 Dis[w]들을 갱신한다.(O(N))
                                3. 모든 노드가 확정되기 까지 1,2 과정을 반복(N번 반복)
                                  -> N^2 +N^2 = O(N^2)

                              2) 빠른 버전 알고리즘(힙을 사용한 최솟값 구하기, 인접 행렬을 인접 리스트(간선을 저장)로 바꿈)

                              1. 의미있는 값만 가지므로 메모리와 시간을 아낄 수 있음
                              2. 시작 노드 주위 이외의 최단거리를 무한대로 놓는다.
                              3. 최단 거리가 확정되지 않은 노드(거리가 무한대) 중 Dis[i] 값이 가장 작은 노드(v)를 고른다(최솟값 찾기(Heap):O(logM))
                              4. 그 노드로부터 이어진 간선들을 이용하여 Dis[w]들을 갱신한다.
                                • 인접리스트에서 갱신하기: O(OutDegree(v)) // outdegree: 나가는 간선의 수(outdegree를 다합치면 간선의 수가 된다)
                               3. 모든 노드가 확정되기 까지 1,2 과정을 반복(N번 반복)
    
    1번 작업은 O(NlogM)
    2번 작업은 MN(간선의 수)
    
    O(NlogM)+ O(M) = O(NlogM+M)

                              다익스트라 알고리즘의 동작 과정, O(N^2)

                              # D: 출발점에서 각 정점까지의 최단 경로 가중치 합을 저장
# P: 최단 경로 트리 저장
def Dijkstra(G,r):# G: 그래프, r: 시작 정점
    D = [INF]*N# 시작점부터 각 노드로 가능 최단 거리를 무한대로 설정
    P = [None]*N# 2 시작지점 부터 해당지점까지의 최단 거리를 구할 수 있게 끔 도와주는 노드
    visited = [False] * N# 3 방문 여부를 모두 False로 설정
    D[r] = 0# 4 시작 지점부터 시작 지점까지의 거리 0으로 설정

    for _ in range(N):# 5 각 노드 연산 때마다 거리값을 갱신
        minIndex = -1
        min = INF
        for i in range(N):
            if not visited[i] and D[i] < min:# 아직 최소거리를 못구했고(visited) 가장 최단경로일 경우, 힙으로 구현시 더빠름
                min = D[i]# 최소 거리 노드로 설정
                minIndex = i
        visited[minIndex] = True# 7 이제 최소거리를 구할 것이므로 visited 설정
        for v, val in G[minIndex]:# 8 해당 node의 간선들에 대해서
            if not visited[v] and D[minIndex] + val <D[v]:# 9 해당 노드의 기존의 최소 거리보다 더 낮은 비용으로 도달할 수 있다면
                D[v] = D[minIndex] + val# 10# 해당 값으로 변경
                P[v] = minIndex# 11 node v의 부모 노드(한번에 한해 어디 노드로부터 이 노드로 오는것이 최단경로인가?) 저장
        # P 집합을 역순으로 올라가서 시작정점까지 가는 경로가 시작 노드 -> 해당 노드로 가능 최단 거리

                              더 빠른 버전, O(NlogM+M)

                              INF = 999999999
def Dijkstra(G, r):# G: 그래프, r: 시작 정점, N: 노드의 수
    N = len(G)
    D = [INF]*N# 1 시작점부터 각 노드로 가능 최단 거리를 무한대로 설정
    P = [None]*N# 2 시작지점 부터 해당지점까지의 최단 거리를 구할 수 있게 끔 도와주는 배열
    visited = [False] * N# 3 방문 여부를 모두 False로 설정
    D[r] = 0# 4 시작 지점부터 시작 지점까지의 거리 0으로 설정
    min_heap = [{"weight": 0, "node": r}]# 5 시작 지점 설정
    while min_heap:# 6 더이상 갱신할 노드가 없을때 까지 실행
# 최소 거리 노드로 설정
        min_node = heapq.heappop(min_heap)# 7 힙을 통해 새로 갱신된 최소 거리 노드 값 구함
        visited[min_node["node"]] = True# 8 이제 최소거리를 구할 것이므로 visited 설정
        for node in G[min_node["node"]]:# 9 해당 최소 거리 노드와 연결된 노드들에 대해           
            if not visited[node["node"]] and D[min_node["node"]] + node["weight"] < D[min_node["node"]]:# 10 해당 노드의 기존의 최소 거리보다 더 낮은 비용으로 도달할 수 있다면
                D[node["node"]] = D[min_node["node"]] + node["weight"]# 11 새로운 최소 거리 경신
       # 12 node의 부모 노드(한번에 한해 어디 노드로부터 이 노드로 오는것이 최단경로인가?) 저장
                P[node["node"]] = min_node["node"]
       # P 집합을 역순은 시작정점까지 가는 경로가 시작 노드 -> 해당 노드로 가능 최단 거리
    return D, P# 13 더이상 갱신할 것이 없는 경우 구한 최소 거리와 최소 거리 경로를 도출


                              #include<iostream>
#include<queue>
#include<vector>
using namespace std;
struct edge{
    int to;
    int weight;
};
vector<edge> edges[300001];

int main(){    
    cin.tie(NULL);
    cout.tie(NULL);
    ios::sync_with_stdio(false);    
    int nodeNum, edgeNum;
    int startNode;
    cin>>nodeNum>>edgeNum>>startNode;
    int max= 0 ;
    for (int i =0; i <edgeNum; i++){
        int from,to,weight;
        cin>>from>>to>>weight;
        edges[from].push_back(edge{to,weight});
        max += weight;
    } 
    max = max * 10;
    int distant[nodeNum+1];
    for (int i = 0; i <= nodeNum; i++){
        distant[i] = max;
    }
    priority_queue<pair<int,int>> heap; // 자동으로 1번째 인자를 비교하여 정렬되는듯하다
    distant[startNode] = 0;
    heap.push({0, startNode});

    while(!heap.empty()){
        int minIndex = heap.top().second; 
        heap.pop();  
        for (int k = 0; k<edges[minIndex].size(); k++){
            edge betweennode = edges[minIndex][k];
            if ((distant[minIndex] +betweennode.weight) < distant[betweennode.to]){
                distant[betweennode.to] = distant[minIndex] +betweennode.weight;
                heap.push({distant[betweennode.to]*-1, betweennode.to}); // -1을 곱해줘서 max heap을 min heap으로 
            } 
        }
    }
    for (int i = 1; i <= nodeNum; i++){
        if (distant[i] < max){
            cout<<distant[i]<<"\n";
        }
        else{
            cout<<"INF\n";
        }
    }
    return 0;
}

                              벨만-포드 알고리즘

                              • 음의 가중치를 포함하는 그래프에서 최단 경로를 구함

                              • 가중치의 합이 음인 사이클은 허용하지 않음, 다익스트라로 최단경로를 구할 수 있다면 벨만-포드로 가능

                              • 출발점에tj 각 정점까지 간선 하나로 구성된 경로만 고려해서 최단 경로를 구함

                              • 그 다음 최대 간선 두개 까지 고려해서 최단경로를 구해나가서 최대 간선 n-1개 까지 고려한 경로들에서 최단 경로를 구함(n은 정점의 개수), 동적 계획법 적용

                              • 만약, 모든 간선과 노드를 고려하여 업데이트한 그래프가 또 다시 최적화될 수 있다면, 그것은 무한 루프를 포함한다는 의미이다.(음의 가중치를 가진 간선에 의해 경로 가중치가 음수로 계속 최적화 되는 경우)

                              • 다익스트라에 비해 많은 시간 소요(O(n^2))

                                &#62; python 구현

                              import sys
input = sys.stdin.readline
INF = 9999999999
nodeNum, edgeNum = map(int, input().split())
edges = [list(map(int,input().split())) for i in range(edgeNum)]
distant = [INF for i in range(nodeNum+1)]
distant[1] = 0# set distance to the first city to the first city to zero
  
for _ in range(nodeNum):# Update distance to each node once with edge information. 
    for edge in edges:
        fr, to, wt = edge
        if (distant[fr] &#38;#62;= INF):continue# if the from node of the edge is unreachable, continue.
 # because Infinity - weight == Infinity
        if (distant[to] &#38;#62; distant[fr] + wt):
            distant[to] = distant[fr] + wt
INFLOOP=False
for edge in edges:
    fr, to, wt = edge
    if distant[fr] &#38;#62;= INF: continue
    if (distant[to] &#38;#62; distant[fr] + wt):# if you can update distance once more,
 # that means, there is an infinity loop in the graph. 
	    print(-1)
        INFLOOP=True
        break
if not INFLOOP:
    [print(-1 if i &#38;#62;= INF else i) for i in distant[2:]]

                              C++ 구현

                              #define INF 987654321
#include<iostream>
struct edge{
    int from;
    int to;
    int weight;
};
using namespace std;
int main(){
    cin.tie(NULL);
    cout.tie(NULL);
    ios::sync_with_stdio(false);
    int cityNum, lineNum;
    cin>>cityNum>>lineNum;
    edge edges[lineNum];
    for(int i = 0; i<lineNum; i++){
        int from, to, weight;
        cin>>from>>to>>weight;
        edges[i] = edge({from,to,weight});
    }
    long long distant[cityNum+1];
    for (int i =0; i<=cityNum; i++){
        distant[i] = INF;
    }
    distant[1] = 0;
  
    for (int i = 0; i<cityNum; i++){
        for (int j =0; j<lineNum; j++){
            if (distant[edges[j].from]>=INF) {
                continue;
            }
            if (distant[edges[j].to] > distant[edges[j].from] + edges[j].weight){
                distant[edges[j].to] = distant[edges[j].from] + edges[j].weight;
            }
        }
    }
  
    for (int i =0; i < lineNum; i++){
        if (distant[edges[i].from] >= INF) continue; // 무한 루프가능 인지 확인할때도 INF 확인 필수
        if (distant[edges[i].to] > distant[edges[i].from] + edges[i].weight){
            cout<<-1<<"\n";
            return 0;
        }
    }
    for(int i = 2; i <= cityNum; i++){
        long long result = distant[i] == INF ? -1 : distant[i];
        cout<<result<<"\n";
    }
    return 0;
}

                              플로이드 워셜 알고리즘

                              • 가능한 모든 쌍에 대해 최단 거리를 구하는 알고리즘 O(N^3)

                              • 모든 쌍에 대한 최단거리를 음의 가중치를 가지는 그래프에서도 가능

                              • 대신 매우 느리다.

                              • 각 시작점과 경유지, 끝점을 모두 돌면서 최단거리 업데이트

                              • 경유지를 loop문의 가장 위로 해야 된다는 점을 주의!

                              import sys
input = sys.stdin.readline
INF = 999999999
citynum = int(input())
edgenum = int(input())
graph = [[INF for j in range(citynum + 1)] for i in range(citynum+1)]
  
for _ in range(edgenum):# Create edge graph
	fr, to, wt = map(int, input().split())
    if (graph[fr][to] &#38;#62; wt):# if the edge has the same start and destination, Update it to a smaller weight.
        graph[fr][to] = wt
  
for start in range(1, citynum+1): 
    for end in range(1, citynum+1):
        if (start==end):# set weight to zero, if start == end
            graph[start][end] = 0
  
# loop all of the nodes.
  
for mid in range(1, citynum+1):# Make sure loop stopover first.
    for start in range(1, citynum+1):
        for end in range(1, citynum+1):
            if (graph[start][end] &#38;#62; graph[start][mid] + graph[mid][end]):
                graph[start][end] = graph[start][mid] + graph[mid][end]
  
for i in graph[1:]:
    for j in i[1:]:
        if j&#38;#62;=INF:
            print(&#34;0&#34;, end=&#34; &#34;)
        else:
            print(j, end=&#34; &#34;)
    print()


                              #include<iostream>
#define INF 987654321
using namespace std;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int cityNum, busNum;
    cin>>cityNum>>busNum;
    long long weights[cityNum+1][cityNum+1];
    for (int i = 1; i <=cityNum; i++){
        for (int j = 1; j<=cityNum; j++){
            if (i==j){
                weights[i][j] = 0;  
                continue;
            }
            weights[i][j] = INF;  
        }
    }
    for (int i=0; i<busNum; i++){
        int from, to, weight;
        cin>>from>>to>>weight;
        weights[from][to] = weights[from][to] > weight ? weight : weights[from][to];
    }
    for (int k = 1; k <=cityNum; k++){
        for (int i = 1; i <= cityNum; i++){
            for (int j = 1; j <= cityNum; j++){
                weights[i][j] = weights[i][k] + weights[k][j] < weights[i][j] ? weights[i][k] + weights[k][j] : weights[i][j];
            }
        }
    }
    for (int i = 1; i <= cityNum; i++){
        for (int j = 1; j <= cityNum; j++){
            if (weights[i][j]==INF){
                cout<<0<<" ";
                continue;
            }
            cout<<weights[i][j]<<" ";
        }        
        cout<<"\n";
    }
    return 0;
  }

                              08 문자열 탐색

                              1. 해싱

                              소개

                              • 파일 시스템에서 파일 등을 찾는 데에 사용

                              • 특정 항목 검색 시, 탐색 키에 대한 산술적 연산으로 키가 있는 위치를 계산하여 바로 찾아가는 방법 (시간 복잡도 O(1)만들 때는 O(S*T)문자열의 길이 + 단어의 길이 )

                              해싱의 방법

                              1) 직접 번지 테이블 (배열)

                              • 자료를 직접 번지 테이블에 저장하는 방법
                              • 전체 키들의 집합이 작은 경우 효율적
                              • 아마 배열에 A~Z중 사용되는 B, D의 위치를 배열에 저장? 하고 나머지는 빈공간에 놓는 방식인듯
                              • 전체 키 집합이 크면 컴퓨터 메모리 공간을 어마어마하게 잡아먹음
                              • 전체 키 집합 U에 비해 실제 키 집합 K가 매우 작으면 배열 메모리 공간 낭비가 심하기 때문,

                              2) 해시 테이블

                              • 집합 U에 비해 실제 사용되는 키들의 집합 K가 작을 때 사용

                              • 직접 번지 테이블보다 메모리 공간이 적게 필요, 세타( k )만큼 필요
                                • 세타는 최적의 경우 시간복잡도

                              • 키 값 k의 자료를 저장할 위치를 계산하는 해시 함수(h) 사용

                              • 키 값 k인 자료를 h(k)의 위치에 저장

                              • 모든 키들의 집합 U를 해시 테이블 T의 위치에 대응시킴

                              • 키 두개가 동일한 위치가 될 수 있는 데 이를 충돌이라고 함.

                              • 다른 키값을 해시 함수로 적용해도 반환된 해시 함수는 같을 수 있음

                              • 해시 함수가 해시 주소를 공평하게 분배해도 해시 테이블에 저장되는 키에 해당하는 자료의 수가 증가하면 충돌은 불가피함

                              해싱 충돌 피하는 방법

                              3) 체이닝(Chaning)

                              • 해시 테이블의 구조를 변경하여 각 버킷에 하나 이상의 키 값을 가지는 자료가 장될 수 있도록 하는 방법
                              • 하나의 버킷에 여러 개의 키값을 저장하도록 하기 위해 연결 리스트를 활용함

                              &#62; 해싱과 체이닝 예시 코드

                              (실습 소스) hash.c


/*
 author: Jung,JaeJoon(rgbi3307@nate.com, http://www .kernel.bz/)
 comments: hash 알고리즘
*/

#include
#include

#define HASHSIZE 256

//구조체선언
struct nlist &#123;
 struct nlist *next; //연결구조체(리스트)
 char *name;                                       //key
 char *phone;
&#125;;

//구조체테이블정의(해시테이블)
static struct nlist *hashtab [HASHSIZE];

//hash 함수: 문자열s를위한해시 값산출
unsigned hash (char *s)
&#123;
 unsigned hashval;

for (hashval = 0; *s != &#39;&#39;&#39;&#39;; s++)  //문자열s의길이만큼반복
       hashval = *s + 31 * hashval;  //문자*s에의존하는난수적인(random) 값

 return hashval &#37; HASHSIZE;  //HASHSIZE 이내의값(0 &#38;#60;= 반환값&#38;#60; HASHSIZE)
&#125;

//해시함수를통하여해시테이블의요소에접근후
//연결된구조체리스트를따라가며반복탐색
struct nlist* lookup (char *s)
&#123;
 struct nlist *np;

 for (np = hashtab[hash(s)];  np != NULL; np = np-&#38;#62;next)
  if (strcmp(s, np-&#38;#62;name) == 0)
                      return np;     //found (찾은위치포인터)
 return NULL;           //not found
&#125;

//문자열s를메모리에할당한포인터반환
char *str_mcopy (char *s)
&#123;
 char *p;
 p = (char *) malloc(strlen(s)+1); //+1 for &#39;&#39;&#39;&#39;
 if (p != NULL)
  strcpy (p, s);
 return p;
&#125;

//해시테이블에구조체할당(저장)
struct nlist* install (char *name, char *phone)
&#123;
  struct nlist *np;
 unsigned hashval;

 if ((np = lookup (name)) == NULL) &#123; //not found (새롭게할당)
           np = (struct nlist *) malloc(sizeof(*np));
           if (np == NULL || (np-&#38;#62;name = str_mcopy (name)) == NULL)
   return NULL;
           hashval = hash (name);
           np-&#38;#62;next = hashtab[hashval]; //현재해시값에있는구조체는다음(뒤)으로연결
           hashtab[hashval] = np;

 &#125; else            //이미존재하면
      free ((void *) np-&#38;#62;phone);              //phone 해제

 if ((np-&#38;#62;phone = str_mcopy (phone)) == NULL)    //phone 다시할당
                  return NULL;
 return np;
&#125;

int main ()
&#123;
 char *name[] = &#123;&#34;John Smith&#34;, &#34;Lisa Smith&#34;, &#34;Sam Doe&#34;, &#34;Sandra Dee&#34;, &#34;Ted Baker&#34;, &#34;JaeJoon Jung&#34;, &#34;James Dean&#34;&#125;;
 char *phone[] = &#123;&#34;521-1234&#34;, &#34;521-8976&#34;, &#34;521-5030&#34;, &#34;521-9655&#34;, &#34;418-4165&#34;, &#34;520-3307&#34;, &#34;425-1020&#34;&#125;;
 int i, n = sizeof(name) / sizeof(name[0]);
 struct nlist *head, *ptr;

 //연결리스트에저장
 for (i = 0; i &#38;#60; n; i++) &#123;
  printf (&#34;&#37;d: &#37;sn&#34;, hash (name[i]), name[i]);
  //구조체에할당
  install (name[i], phone[i]);
 &#125;

 //해시테이블에연결된리스트출력
 printf (&#34;nHash Table List n&#34;);
 for (i = 0; i &#38;#60; HASHSIZE; i++) &#123;
  head = hashtab [i];
  for (ptr = head; ptr != NULL; ptr = ptr-&#38;#62;next) &#123;
             printf(&#34;&#37;d: &#37;s, &#37;sn&#34;, i, ptr-&#38;#62;name, ptr-&#38;#62;phone);
  &#125;
 &#125;

 printf (&#34;nHash Table Search n&#34;);
 ptr = lookup (&#34;JaeJoon Jung&#34;) ;
 printf(&#34;found: &#37;s, &#37;sn&#34;, ptr-&#38;#62;name, ptr-&#38;#62;phone);

 printf (&#34;nPress any key to end...&#34;);
 getchar();
 return 0;
&#125;



(실행 결과) hash .c

174: John Smith
46: Lisa Smith
57: Sam Doe
23: Sandra Dee
44: Ted Baker
210: JaeJoon Jung
10: James Dean

Hash Table List
10: James Dean, 425-1020
23: Sandra Dee, 521-9655
44: Ted Baker, 418-4165
46: Lisa Smith, 521-8976
57: Sam Doe, 521-5030
174: John Smith, 521-1234
210: JaeJoon Jung, 520-3307

Hash Table Search
found: JaeJoon Jung, 520-3307

Press any key to end...


-


출처 : 테크월드(http://www.epnc.co.kr)

                              2) 개방 주소법(Open Adderess)

                              • 해시 함수로 구한 주소에 빈 공간이 없어 충돌이 발생하면 그 다음 위치에 빈 공간이 있는지 조사하는 방법

                              • 빈 공간이 있을 경우 : 탐색키에 대한 항목 저장

                              • 빈 공간이 없을 경우 : 공간이 나올 때까지 탐색 반복

                              2. 문자열 탐색

                              • 문자열 매칭(패턴 매칭)이란, 텍스트 문자열(t)에 패턴 문자열(p)가 포함되 있는지 찾는것

                              고지식한 패턴 검색 알고리즘( 단순 검색)

                              • 본문 문자열을 처음부터 끝까지 차례대로 순회하면서 패턴 내의 문자들을 일일이 비교하는 방식의 알고리즘

                              • 패턴 길이 : m, 텍스트 길이: n일 때 O(m*n)만큼의 시간이 걸림

                              • 불일치가 발생할 시, 다음 검색 지점은 이전 시작의 다음 위치, 패턴은 항상 처음에 시작

                                고지식한 패턴 검색 알고리즘

                              // p[ ]: 패턴, t[ ]: 텍스트
// M: 패턴의 길이, N: 텍스트의 길이
BruteForce(int p[], int t[])&#123;
    int i = 0;
    int j = 0;
    while(j &#38;#60; M and i &#38;#60;N)&#123;
        if (t[i] != p[j])&#123;
            i = i - j;
            j = -1;
        &#125;
        i++;
        j++;
    &#125;
    if (j == M)&#123;
    return i - M;
    &#125;
    else return i;
  &#125;

                              카프-라빈 알고리즘

                              • 문자열 검색을 위해 해시 함수를 이용하는 알고리즘

                              • 패턴의 해시 값과 텍스트 내의 패턴 길이만큼의 문자열에 대한 해시 값 비교

                              • 최악의 시간 복잡도는 패턴 길이 : m, 텍스트 길이: n일 때 O(mn)이나 평균적으로는 선형임
                                1) 주의할 점

                              • 해시 값을 구할 때, 새로 추가되는 문자와 그 전에 계산한 값을 이용해서 구함

                              • 지나간 수는 버리고 새로 추가될 값을 비교하여 구함

                              • 처음 해시 값을 구할 때 찾고자 하는 문자열에서 패턴 길이만큼 읽어서 구함

                              • 패턴의 길이가 커지면 길이를 일정 자릿수로 맞추기위해 %(모듈러) 연산함

                              • 해시 값이 일치할 경우, 실제 문자열이 일치하는 지 검사해야함(해시 특성상 문자열이 다른데, 결과값이 같을 수도 있음)

                                내가 구현한 카프라빈 알고리즘

                              #define _CRT_SECURE_NO_WARNINGS
#include &#38;#60;stdio.h&#38;#62;
#include &#38;#60;Windows.h&#38;#62;
#include &#38;#60;time.h&#38;#62;
#define HASH2

int hash(char* str,int len);
int hash2(char* str, int len);
int strlen(char* str);
int strcmp(char* str, char* src, int len);

int main() &#123;

    clock_t start, end;
    start = clock();
    
    char src[6000];
    freopen(&#34;string.txt&#34;,&#34;r&#34;,stdin);
    gets(src, sizeof(src));
    
    char* str = &#34;Syrup&#34;;
    // hash : 최대 24글자 정도 사용 가능, hash2 : 훨씬 긴 문자열 가능하지만 해쉬 충돌이 많이 일어나 속도가 조금 느릴듯?
    int len = strlen(str);

#ifdef HASH2
    int strhash = hash2(str, len);
    int thash = hash2(src, len);
#else
    int strhash = hash(str, len);
    int thash = hash(src, len);
#endif // HASH@
    int idx = 0;

    while (*(src+idx+len-1)) &#123;
        if (thash == strhash) &#123;
            if (strcmp(str, src + idx, len)) &#123;
                printf(&#34;&#37;d\n&#34;, idx);
                printf(&#34;&#37;s\n&#34;, (src + idx));
                break;
            &#125;
            idx++;
        &#125;
        else &#123;

#ifdef HASH2
            thash -= *(src+idx) + *(src+idx) * 31;
            thash += *(src + idx + len) + *(src + idx + len) * 31;
#else
            thash -= *(src+idx) &#38;#60;&#38;#60; (len-1);
            thash = thash &#38;#60;&#38;#60; 1;
            thash += *(src+idx+len);
#endif // HASH@
            idx++;
        &#125;
    &#125;
    printf(&#34;done\n&#34;);
    end = clock();
    printf(&#34;타이머: &#37;f&#34;, ((float)(end - start) / CLOCKS_PER_SEC));
    return 0;
&#125;
int strcmp(char* str, char* src, int len) &#123;
    for(int i =0; i&#38;#60;len; i++) &#123;
        if (*str != *src ) &#123;
            return 0;
        &#125;
        if (*str == 0 || *src == 0) &#123;
            return 0;
        &#125;
        str++;
        src++;
    &#125;
    return 1;
&#125;
int strlen(char* str) &#123;
    int idx = 0;
    while (*str != 0) &#123;
        str++;
        idx++;
    &#125;
    return idx;
&#125;
int hash(char* str, int len) &#123;
    int hashVal;
    int idx = len-1;
    for (hashVal = 0; idx &#38;#62;= 0; idx--) &#123;
        hashVal += (*str++ &#38;#60;&#38;#60; idx); 
    &#125;
    return hashVa&#37; 1000000007l; // 해쉬 꿀팁! : m(모듈러로 나누는 값, 여기서는 1000000007)은 d(d^x승으로 곱해주는 값, 여기서는 2)와 서로소이며 아주 큰 수이면 좋다.  unsigned long long으로 지정하면, overflow로 인하여 m은 2^64처리가 된다, d는 257, 259 ... 5384같은 큰값을 하면 된다.
&#125;
int hash2(char* str, int len) &#123;
    int hashVal = 0;
    for (int idx = 0; idx &#38;#60; len; idx++) &#123;
        hashVal +=*str + *str*31;
        str++;
    &#125;    
    return hashVal;
&#125;

                              KMP 알고리즘

                              • (Knuth-Morris-Pratt)의 앞글자를 따서 만듦
                              • 불일치가 발생한 텍스트 문자열의 앞에 어떤 문자가 있는지 알고 있으므로 다시 비교하지 않고 매칭 수행
                              • 불일치가 발생하면 다음 비교 위치를 미리 계산, 불필요한 시작을 최소화함
                                • 패턴의 모든 위치마다 불일치가 발생하면 이동할 위치를 계산하여 저장
                                • 패턴의 길이만큼의 배열 필요
                              • 시간 복잡도는 패턴 길이 : m, 텍스트 길이: n일 때 O(m+n)
                              • 아호코라식 이라는 상위호환 알고리즘이 있다. 이것이 기반
                                1) 아이디어
                              • 패턴의 접두어와 실패한 문자열에서 슬라이싱한 패턴의 접미어를 비교하여 이동
                              • 실패 함수(f(i), Failure function)
                                • f(i)는 패턴 P의 P[1, i]에서 가장 긴 접두사와 접미사가 같은 것의 길이
                                  abacaba 의 경우 0, 0,1,0,1,2,3이다. 각각
                                  a는 기본 0, b는 ‘ab’에서 공통된 접두사와 접미사의 길이가 0,
                                  a는 aba에서 가장 긴 접두사 a와 접미사 a 길이가 1
                                  c는 ‘abac 가장 긴접두사와 접미사의 길이가 0
                                  마지막 a의 경우 abacaba에서 접미사aba와 접두사aba가 같으므로 3
                              • i번째(1부터 시작) 패턴이 틀리면 (i-1) - f(i-1) 칸 만큼 이동
                                - 왜? : abacaba에서 c 부문이 틀렸다고 가정하면 c의 이전 문자(마지막까지 매치된 문자) a의 f(3)는 1이다, 그냥 3칸을 이동시키면 일치했던 aba 중, 마지막 a가 3번째 a와 일치하므로 그 부분부터 비교를 해야한다. 그러므로 3칸 이동 후, 접미사 길이 만큼인 1만큼 빼서 이동하는 것이다.
                                -
                              • 매칭이 실패했을 때 돌아갈 곳을 계산한 뒤, 그것을 next 배열에 저장한다.
                              • next 배열에는 공통되는 접두어와 접미어 수만큼 저장하는 듯
                              • 그리고 마지막은 0
                              • 공통되는 접두어와 접미어가 있는지 확인하여 저장한다.
                              • 맨 처음 글자의 next는 -1인데, 패턴 처음 위치 불일치 시, 고지식한 패턴 검색과 유사하게 동작하기 위함
                              • 만약 1글자만 찾고 끝나는게 아니라 전체에서 단어의 수를 찾고 싶으면 찾을 문자열 패턴 마지막에 .이나 유니크한 다른 문자를 추가한다. (ex)abacabc=>abacabc.)
                                • 앞의 모든 문자열을 비교하고 .을 비교할 때가 되면 그 문자열은 일치하는 것이므로 count를 증가시켜주거나 위치를 배열에 저장한다. 그리고 .은 무조건 없으므로 계속 탐색하게 된다.

                              KMP 알고리즘 전처리 함수(next 배열(실패 함수) 구하기)

                              // p[] : 패턴, M : 패턴의 길이
// next[] : 불일치가 발생하면 이동할 위치를 저장
void KMP_Preprocess(char p[], int next[])&#123;
    int i = 0;// 최초 글자는 -1로 시작
    int j = -1;// j : 일치한 문자의 수
    next[i] = -1;

    while(i&#38;#60;M)&#123; // 패턴의 길이만큼
        while(j &#38;#62;= 0 &#38;&#38; p[i] != p[j])
            j = next[j];//패턴i,j의 위치값 비교
        ++i;
        ++j;
        next[i] = j;
    &#125;
&#125;
                              • 실패 함수 구하기 O(M) :

                              KMP 알고리즘 패턴 매칭

                              // t[]:텍스트, N: 텍스트 길이, p[]: 패턴, M: 패턴 길이
// next[]: 불일치가 발생하면 이동할 위치를 저장
int KMP_Search(char t[], char p[], int next[])&#123;
    int i = 0;
    int j = 0;
    while(i &#38;#60; N-M+1)&#123;
        while (j &#38;#62;= 0 &#38;&#38; t[i] != p[j])
            j = next[j];
        ++i;
        ++j;
        if (j==M) return i-j; // 패턴 찾음 첫글자 인덱스 리턴
    &#125;
    return -1;//일치 하는 것이 없음
&#125;

                              접두어와 접미어란?

                              • 접두어와 접미어는 문자열의 길이만큼 존재

                              • 모든 부분 문자열은 모든 접미어들의 모든 접두어

                                문자열이 ‘abcdabc’ 일 때, 접두어와 접미어 예시

                              접두어 접미어
                              a c
                              ab bc
                              abc abc
                              abcd dabc
                              abcda cdabc
                              abcdab bcdabc
                              abcdabc abcdabc

                              보이어-무어 알고리즘

                              • 대부분의 상용 소프트웨어에서 채택하고 있는 알고리즘

                              • 오른쪽 끝에서 왼쪽으로 문자열을 비교하는 알고리즘

                              • 앞부분보다 끝부분에 불일치가 일어날 확률이 높은 성질을 이용

                              • 패턴의 오른쪽 끝 문자에서 불일치 발생 시, 텍스트의 문자가 패턴 내에 없으면 이동거리는 패턴의 길이가 됨

                              • 오른 쪽 끝 문자가 불일치 한데, 이 문자가 패턴내에 존재할 경우

                                1) 패턴에서 일치하는 문자를 찾아 서로 일치되도록 점프
                                2) 어느 정도 점프해야하는지 미리 배열을 만들어 놓아야함

                              • 이를 스킵배열이라고함(오른쪽 끝 문자 불일치, 그리고 해당 문자가 패턴내에 없을시, 이동해야하는 칸수 적어놓음)

                              • 시간 복잡도는 최악의 경우 O(mn) 하지만 보통 세타(n)보다 적음

                              3. 트라이(Trie)

                              트라이 도식화

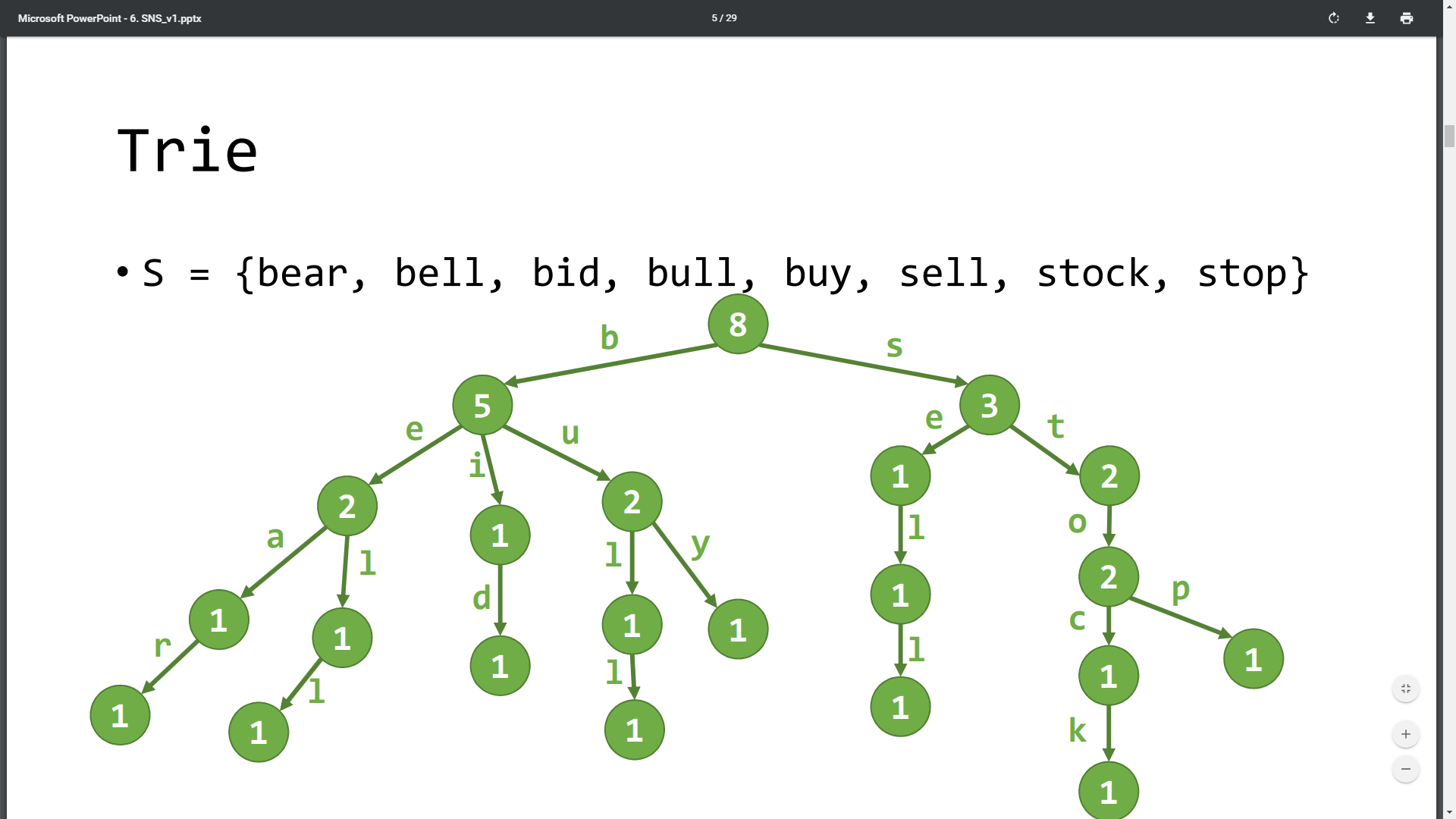
                              • prefix(접두어) tree 라고도 함, 문자열의 집합을 표현하는 트리, 문자열을 찾을때 사용함

                              • 정보검색(Retrieval)에서 이름을 따옴 (트라이라고 발음함)

                              • 트라이의 각 간선은 하나의 문자에 대응

                              • 같은 노드에 나오는 간선들은 같은 라벨(같은 문자)을 갖지 않음

                              • 루트에서 단말 노드까지 이른 경로가 하나의 문자열

                              • 즉 단말 노드는 문자열 하나

                              • 각 노드에 최종 단말노드의 갯수(자식들의 합)를 적어놓을 수 있다.

                                • 단어가 끝나는 단말노드에 색칠(다른 표시)를 통해 단어의 끝임을 표현해줘야함(필요할 시)

                              알고리즘

                              • 문자열 추가 시, 단말 노드를 추가하고, 각 노드에 적혀있는 단말노드 갯수를 적어놓은 것을 추가 해줘야한다.

                                트라이 예시

                              #define NM 1000000 // 정적으로 미리 해놓지 않으면(정적 할당) 메모리를 새로 할당하는데 시간이 엄청나게 걸린다. (새로 공간을 만들어놓고 통으로 복사함)
  struct NODE &#123;
    int next[26]; //자식을 포인터(주소값)로 넣으면 cache freindly 하지 않으므로 새로 자식을 추가할 때, 노드 생성 시기가 다르므로, 메모리상 주소가 제각각 위치가 되어 메모리가 참조하는데 엄청나게 느려진다. 그래서 번호로 기억하게 만들면 10배 이상 빨라진다.
    int cnt;
    void init() &#123;
        for (int i = 0; i &#38;#60; 26; i++)
        next[i] = -1; // 초기에는 어떤 자식도 없다
        cnt = 0; // 어떠한 단어도 밑에 가지고 있지 않다.
    &#125;
  &#125;trie[NM];
  int root = 0, trieN;


void init(void) &#123;
    root = 0; // 루트 날리기
    trieN = 0; // 트라이 날리기(모든 노드의 갯수)
    trie[0].init();
&#125;

//재귀적으로 단어 추가
void myInsert(int trieIdx, int bufIdx, int buffer_size, char *buf) &#123;
    trie[trieIdx].cnt++;
    if (bufIdx == buffer_size) return;// 단어를 끝까지 갔다는 뜻, 추가로 리턴대신 색칠 가능(단말노드로 표시)
    int ch = buf[bufIdx] - &#39;a&#39;;
    if (trie[trieIdx].next[ch] == -1) &#123;// 추가로 갈 수 있는 간선이 없다면(글자가 없다면)
        trie[trieIdx].next[ch] = ++trieN;// 추가로 정점을 추가해주고 가르키게 해줌
        trie[trieN].init(); // 새로운 노드 생겼으므로 초기화
    &#125;
    myInsert(trie[trieIdx].next[ch], bufIdx + 1, buffer_size, buf);
    // 있으면 다음 글자를 찾아가라
&#125;

void insert(int buffer_size, char *buf) &#123;
    myInsert(root, 0, buffer_size, buf);
&#125;

// 문자열 찾기 알고리즘
int query(int buffer_size, char *buf) &#123;
    int trieIdx = root;
    for (int i = 0; i &#38;#60; buffer_size; i++) &#123;
        int ch = buf[i] - &#39;a&#39;;
        trieIdx = trie[trieIdx].next[ch];
        if (trieIdx == -1) return 0; // 문자열이 없다면 0을 리턴
    &#125;
    return trie[trieIdx].cnt; // 있다면 해당 단말노드 번호를 리턴
&#125;

                              접미어 트라이

                              • 문자열의 모든 접미어를 Trie로 표현함
                              • 길이가 n인 문자열 A = a0~an-1, 접미어도 n-1개가 존재
                              • 부분 문자열 검사(ba가 abac의 부분인가?)
                                • 한 문자씩 루트에서 대응되는 간선 따라가면 됨
                              • 두 접미어의 최장 공통 접두어 찾기 (abac, ac의 최장공통 접두어)
                                • 두 접미어의 끝 글자에 대응하는 노드 선택 뒤, 가장 가까운 공통 조상을 찾으면 공통 접두어가 됨
                              • 사전적 순서로 정렬된 k번째 접미어는?
                                • 깊이 우선 탐색(BFS) 문자열은 사전적 순서로 정렬됨
                                • 생성된 문자열이 아닌 인덱스 값 저장(보통 접미어 시작위치)
                              • 등에 접미어 트라이가 유용함

                                4. 접미어 트리(Suffix Tree)

                              • 하나의 문자열의 모든 접미어를 포함하는 트라이(Trie)의 표현
                              • 1973년, Weiner에 최초로 소개되었고, 이후 공간 복잡도를 줄이기 위해 접미어 배열이 알려짐
                              • 문자열 연산에 필요한 알고리즘을 빠르게 구현 가능
                              • 문자열 매칭, 부분 문자열 매칭, 최장 공통 부분문자열에 사용 가능

                                압축된 트라이(Compressed Trie)

                              • 노드와 간선을 부분 문자열로 압축함
                              • 하나의 노드를 하나의 간선으로 표현함, 원래 한 간선에 1글자지만 그냥 eef 가 한 간선으로 표현

                                6.압축

                                2. Run-Length Decoding 알고리즘

                              • 동일한 값(코드)이 몇 번 반복 되는가를 나타내는 방식(bmp 확장자 방식)
                              • 예) ABBBBBCC = A1B7C2

                                Run-Length Encoding 알고리즘
                                ```c
                                // MAXCOUNT = 255 최대 표현 가능 숫자
                                void RLEncoding(char input[]){
                                char count = 1; // 연속적으로 나타나는 코드 값의 횟수 저장(1~255까지 표현)
                                char prev = '\0'; // 바로전에 나온 코드값 저장
                                while (remains(input)){
                                char curr = getnext();// 코드값 하나 1바이트씩 읽음
                                if (prev == curr && count &#60; MAXCOUNT)
                                ++count;
                                else{
                                output(prev, count);
                                count = 1;
                                }
                                prev = curr;// 이전 코드값을 prev에 저장함
                                }
                                output(curr, count);// 마지막 코드 값을 저장

                              }

                              > Run-Length Decoding 알고리즘

```c
void RLDecoding()&#123;
    int curr = 코드값;
    int count = 갯수;
    while(인코딩된 데이터가 남아있으면)&#123;
        curr = 다음 코드 읽기;
        count = 그 코드의 갯수 읽기; //ex)A6의 6
        while(count &#38;#62; 0)
            output(curr); // 현재 코드 갯수만큼 출력
            count--;
    &#125;
&#125;

                              3. 허프만 코드(Huffman Code)

                              • 기호의 빈도와 허프만 트리가 주요 개념
                                1) 기호의 빈도 : 전체 데이터 안에서 기호가 차지하는 비율

                              2) 허프만 트리 : 각 기호에 이진 코드를 부여하기 위해 생성하는 이진 트리

                              고정길이 코드와 접두어 코드

                              3) 고정 길이 코드란? : 기호에 대응하는 코드값의 길이가 똑같은 코드 체계(ex) ASCII)

                              4) 접두어 코드(Prefix Code) : 가변 길이 코드의 한 종류로 어느 코드가 다른 코드의 접두어 되지 않는 코드 체계 Ex) 코드집합

                              • 예를 들어 a~f까지 6글자가 5000~45000개씩 포함되어있는 파일에서 빈도수가 가장 높은 것을 가변길이 코드 용량이 낮은것 순으로 할당하면 효율적이게 저장 가능
                              허프만 코드의 생성과 허프만 트리

                              • 탐욕 알고리즘 기법에 의해 허프만 트리 생성

                              • 단말 노드는 기호와 빈도를 저장, 부모 노드는 빈도만 저장

                              09 동적 계획법의 소개

                              귀납 기본(Induction base) n = 1(혹은 n = 0)에 대해 등식이 성립함을 증명
                              귀납 가정(Induction hypothesis) 임의의 n에 대해 등식이 성립한다고 가정
                              귀납 단계(Induction step) 등식이 n+1에 대해서도 성립함을 증명
                              비둘기 집의 원리를 통해서 동적계획법이 필요한 문제인지 증명 가능(중복되는 값이 많은가)

                              인덱스트리를 통해서 좀더 빠르게 짤 수 있음

                              표를 만든다 라는 느낌

                              10 동적 계획법의 적용

                              11 동적 계획법의 활용

                              12 NP-Complete

                              13 근사 알고리즘

                              14 정수론과 최적화

                              • stack 메모리(함수나 {} 중괄호 안의 변수는 이곳에 할당 된 뒤, 종료시 삭제됨 아주 작지만 빠름)
                              • 정적 메모리,heap,(전역변수 함수 바깥에 있는 메모리는 이곳에 할당됨, 크기가 아주 큼, 조금 느림, 함수 내부 변수도 static 키워드를 통해 이곳에 할당 가능)