시간 복잡도

Sep 22, 2021

시간 복잡도(Time complexity)

---

Introduction to Algorithm, 3rd, Cormen을 토대로 정리한 내용입니다.

앞서 알고리즘 연산 비용 구하기 글을 보고 오는 것을 추천

시간 복잡도(Time complexity)란?

---

시간복잡도는 알고리즘이 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 점근적인 표기법으로 나타내어 정량화한 것이다.

✍ 시간 복잡도 표기법의 그래프 예시

[Fig 1]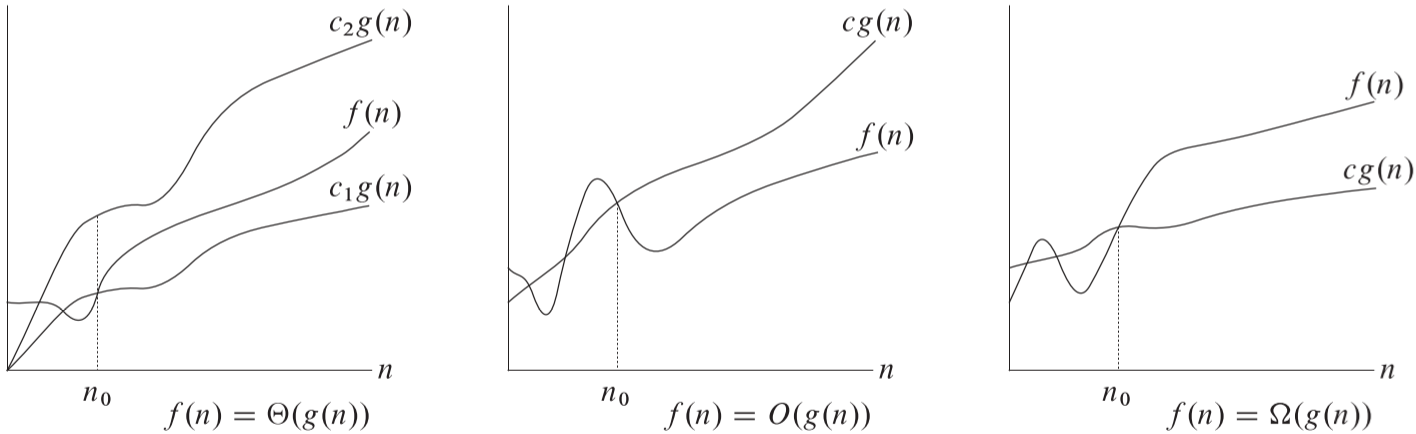

주로 빅오(big-O) 표기법으로 표현하며, 이외에도 빅오메가(big-$\Omega$) 표기법, 빅세타(big-$\Theta$) 표기법이 존재한다.

➕ 표기법의 오용

사실, 여기 설명할 모든 표기법은 엄밀히 말하면 함수들의 집합이고, $f(n)$은 $O(n^2)$의 복잡도를 무한한 수의 함수 중 하나이기 때문 함수 $f(n)$에 대하여 $f(n)\in O(g(n))$으로 표현하는게 맞지만, $f(n)=O(g(n))$으로 오용되곤 한다.

또한, 상수 시간을 의미하는 $O(1)$ 또한 오용이며, 정확히는 $O(n^0)$이 옳은 표기 (무한으로 발산할 수 있는 변수 n을 표기해줘야 한다. )

하지만 나는 앞으로 위 두 표기 모두를 정상으로 표기할 것이다.

$\Theta-표기법$

빅세타(big-$\Theta$) 표기법은 알고리즘 실행 시간에 대한 점근적 상한과 하한을 표기하는 표기법이다.

주어진 함수 $g(n)$(주로 알고리즘 시간 복잡도의 최고차항)에 대하여 $\Theta(g(n))$은 다음과 같은 함수의 집합으로 정의된다.

$\Theta(g(n))={f(n):모든\ n\geq n_0에\ 대해\ 0\leq c_1g(n)\leq f(n)\leq c_2g(n)를\ 만족하는\ 양의\ 상수\ c_1,c_2,n_0가\ 존재}$
즉, 우리가 구한 알고리즘의 연산비용 다항식 $f(n)$의 충분히 큰 수 $n_0$부터 그래프는 점근적 표기인 $g(n)$의 서로 다른 정수배 $c_1,c_2$의 그래프에 둘러쌓인 형태가 되야 한다. (Fig 1 좌)

이를 $g(n)$이 $f(n)$의 asymptotically tight bound(점근적 극한 한계?)라고 한다.

즉, 빅세타(big-$\Theta$) 표기법은 특정 상수 c를 바꾸는 것으로 최대 예상 비용과 최소 예상 비용을 예측할 수 있는 함수를 의미한다.

$\Theta$-표기법 예시

\[c_1n^2\leq \frac{1}{2}n^2-3n\leq c_2n^2 \rightarrow divide\ all\ item\ into\ n^2 \\ =c_1\leq \frac{1}{2}-\frac{3}{n}\leq c_2\]

위의 경우 $c_2$가 $1/2$이상일 경우, $n$은 0 이상부터 성립하게 되므로 $f(n)\in \Theta(n^2)$이다.

\[c_1n^2\leq 6n^3\leq c_2n^2 \rightarrow divide\ all\ item\ into\ n^2 \\=c_1\leq 6n\leq c_2\]

위의 경우 $c_2$가 아무리 크더라도, $c_2$를 넘어서는 양수 $n$이 존재하므로, $f(n) \notin \Theta(n^2)$이다.

O-표기법

빅오(big-O) 표기법은 최악의 상황에서의 점근적 상한을 표기하는 표기법이며, 가장 널리 사용된다.

$O(g(n))$은 다음과 같은 집합으로 정의된다.

$O(g(n))={f(n): 0\leq f(n) \leq cg(n)을\ 만족하는\ 양의\ 정수\ c, n_0가\ 존재한다.}$

즉, 빅오(big-O) 표기법은 점근적으로 함수의 상한을 알려준다.(Fig 1 중앙)
앞서 설명한 $\Theta$-표기법이 상한과 하한을 알려주므로, $\Theta(g(n)) \in O(g(n))$이 성립한다.

➕ 상한과 하한을 모두 알려주는 $\Theta$-표기법과 비교하여 상한만 알려주는 O-표기법을 더 많이 사용하는 이유?

$\Theta$ 표기법은 모든 입력에 대해 보장하지 않는다.

예를 들어, 삽입 정렬은 최악의 상황, 보통 상황에서 $\Theta(n^2)$이다.
하지만 모든 원소가 이미 정렬되어 있는 최적의 상황에서 $\Theta(n)$이다.

따라서 $\Theta$ 표기법으로 “삽입 정렬은 최악과 보통 상황에서 $\Theta(n^2)$, 최적의 상황에서는 $\Theta(n)$이다”라고 두개로 나누어 표기해야 옳은 표현이며 복잡하기 그지없다.

반면에 $O$-표기법은 애초에 성능의 하한을 고려하지 않기 때문에 삽입정렬은 $O(n^2)$이다. 최고차항이 1인 다항식 $an+b$ 또한 $O(n^2)$에 속하기 때문이다.

$\Omega$-표기법

빅오메가(big-Omega) 표기법은 최적의 상황에서의 점근적 하한을 표기하는 표기법이다.(Fig 1 우측)

$\Omega(g(n))={f(n): n\geq n_0일\ 때,\ 0\leq cg(n)\leq f(n)를\ 만족하는\ 양의\ 상수\ c와\ n_0가\ 존재한다.}$

이외에도

• 빅오 표기법과 비슷하나 점근적으로 근접하지 않은 o(리틀-오)-표기법

  • 즉, 최악의 상황의 연산 비용보다 많은 비용을 표기함. 예를 들어, 식 $f(n)$이 $2n$일 경우, 빅오 표기법으로는 $O(n)$이지만, 리틀오 표기법으로는 $o(n)$이 성립하지 않으며, $o(n^2), o(n^3),\dots$이 가능하다.

  • 수학적 정의로는$\lim_{n\rightarrow\infty}=\infty$이 성립할 때, $o(g(n))=f(n)$이 성립.

• 빅오메가 표기법과 비슷하나 점근적으로 근접하지 않은$\omega$(리틀 오메가)-표기법

  • 즉, 최적의 상황의 연산 비용보다 적은 비용을 표기함. 예를 들어 식 $f(n)$이 $2n^2$일 경우, 빅오메가 표기법으로는 $\Omega(n^2)$이지만, 리틀 오메가 표기법으로는 $\omega(n^2)$이 성립하지 않으며, $w(n), w(n^0),\dots$이 가능하다.

  • 수학적 정의로는 $\lim_{n\rightarrow\infty}=0$이 성립할 때, $\omega(g(n))=f(n)$이 성립.

이 존재한다.

최악의 상황(=big-O notation)을 기준으로 분석하는 이유

알고리즘 연산 비용 구하기 에서 구한 삽입 정렬의 연산비용 다항식은 우리가 익히 들어왔던 시간복잡도 빅오(big-O) 표기법에 의하면 $O(n^2)$으로 표기.

빅오 표기법은 이전 최악의 상황에서의 비용값 중 최고차항만 간략표기하여 구함.
입력값이 충분히 커지면, 같은 최고차항을 가진 식 간의 비용 비교시, 계수와 상수의 영향이 거의 의미가 없어지기 때문.

• 예를 들어 상수, 계수가 큰 $100n+200$의 알고리즘 1과 차수가 큰 $n^2$의 알고리즘 2가 존재할 때

  • $n= 100$ 까지는 알고리즘 1이 더욱 효율적.

  • $n = 101$ 부터는 알고리즘 2가 더욱 효율적.

    입력값이 적은 경우, 어느쪽이나 연산속도가 빠름, 입력값이 크다면 연산속도가 더욱 빠른 알고리즘 2를 선호 $\rightarrow$ 결국 최고차항이 작은 알고리즘이 더욱 유리하다.

알고리즘을 평가 시, 평균적인 상황, 최적의 상황이 아니라, 최악의 상황을 기준으로 분석하는 이유

• 어떠한 입력값이든지, 필요 시간의 상한을 예상하기 위해. 즉, 연산 완료를 보장받을 수 있는 가장 빠른 시간이기 때문에.

• 의외로 최악의 상황에서의 연산은 실제 업무의 상황에서 평균적인 상황 만큼이나 자주 나타난다.

  • 예를 들어, 검색 엔진이나 데이터베이스에서 특정 항목을 색인할 때, 해당 항목이 존재하지 않다면, 모든 항목을 찾아보게 된다.(=최악의 상황에서의 연산)

• 평균적인 상황에서의 연산 비용은 의외로 최악의 상황에서의 연산 비용과 큰 차이가 나지 않는 경우가 많다.

  • 예시를 위해 평균적인 상황에서의 삽입 정렬의 비용은 키값 A[j]가 미리 정렬된 부분 배열의 중간까지만 비교하며, 연산 횟수 $t_j$는 $j/2$이다.
    삽입 정렬의 총 비용 다항식을 구하면 계수와 상수가 조금 작을 뿐이지 이차 함수인 $O(n^2)$의 성능임.

주요 알고리즘들의 시간 복잡도

✍ Fig 2. 입력 크기 $n$과 함수의 값에 대한 그래프, 빅오 복잡도 그래프 또한 이에 비례한다.

정렬

정렬 방법	최적	평균	최악	공간 복잡도
선택(selection)	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(n^2)$
버블(bubble)	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(n)$
삽입(insert)	$O(n)$	$O(n^2)$	$O(n^2)$	$O(n^2)$
병합(merge)	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$
퀵(quick)	$O(n\log n)$	$O(n\log n)$	$O(n^2)$	$O(n\log n)$
힙(heap)	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(n)$
쉘(shell)	$O(n^{1.25})$	$O(n^{1.25})$	$O(n^{1.25})$	$O(n)$

그래프

	최적	평균	최악	공간

기타

	최적	평균	최악	공간