병합 정렬

Jul 11, 2021

Merge Sort(병합 정렬)

🗣️ 출처

_Introduction to Algorithm, 3rd, Cormen_을 토대로 정리한 내용입니다

병합 정렬은 divide-and-conquer 알고리즘을 이용하여 재귀적으로 정렬하는 알고리즘이다.

전반적으로 퀵정렬보다 뒤떨어지고 데이터 크기 만큼 메모리가 더 필요한다.

안정된 정렬(stable sort)이므로, 만약 같은 크기의 원소가 둘이 존재하면, 둘의 선후 관계가 바뀌지 않는다.

Merge 함수

먼저 Merge 함수이다. Merge-Sort 함수 내부에 실행될 함수로, 나눈 두 개의 정렬된 배열을 하나로 합치는 역할을 한다.

Merge(A,p,q,r)
	n1=q-p+1
	n2=r-q
	//let L[1..n1+1] and R[1..n2+1] be new arrays
	for i = 1 to n1
	    L[i] = A[p+i-1]
	for j = 1 to n2
	    R[j] = A[q+j]
	L[n1+1] = inf
	R[n2+1] = inf
	i = 1
	j = 1
	for k = p to r // 루프 불변성 대상 루프
	    if L[i]<=R[j]
	        A[k] = L[i]
	        i = i + 1
	    else A[k] = R[j]
	        j = j + 1

위 과정의 시간 복잡도는 $O(n)$이다.

• 존재하는 for loop들이 모두 n에 비례하여 진행됨 즉, n에 대한 선형 함수꼴
• 이외의 코드는 모두 상수 시간임.

Merge 함수의 루프 불변성

이때, 17번째 줄부터 마지막 까지의 for 루프의 루프 불변성은 다음과 같이 보존된다.

루프 불변성(Loop invariant) 가정 :

오름차순 병합 정렬에서 부분배열 $A[p..k-1]$은 $L[1..n1+1]$과 $R[1..n2+1]$의 원소들 중 $k - p$ 개의 가장 작은 원소들로 이루어져 있으며, 정렬되어 있다. 또한, $L, R$ 배열 내에서 현재 아직 $A$ 배열에 추가되지 않은 원소들인 $L[i]$와 $R[j]$는 $L, R$ 배열 내에서 가장 작은 원소이다.

초기화에서의 루프 불변성:

루프에 진입하면서 $k = p$이며, $A[p…k-1]$은 비어있으므로, $k-p(0)$개의 가장 작은 원소들로 이루어져 있고, 정렬되어 있다. 또한 $L$과 $R$ 배열은 각각 정렬되어 있으므로, $L[1], R[1]$은 각자 배열에서 가장 작은 원소이다. 즉, 루프 불변성이 보존된다.

유지에서의 루프 불변성:

먼저 $L[i] <= R[j]$인 경우, $L[i]$는 $A[k] = L[i]$ 이전에 $A$에 포함되지 않은 $L$ 내에서 가장 작은 원소이며, $A[k] = L[i]$ 이후에 $A[p…k]$는 $k-p+1$개의 정렬된 가장 작은 원소들을 가지고 있게 된다. 이후 $k$와 $i$가 1씩 증가하면서 루프 불변성을 보존한다.

$R[j] < L[i]$인 경우, 16, 17번째 줄의 코드가 똑같은 행동으로 루프 불변성을 보존한다.

종료에서의 루프 불변성:

$k = r + 1$이 되면서, $A[p..k-1]$ 즉, $A[p..r]$은 $k-p=r-p+1$개의 $L[1..n1+1], R[1..n2+1]$에서 가장 작은 정렬된 원소들을 가지게 된다. 이때 $L,R$에는 각각 무한대의 원소만 하나씩 가지게 되므로, 루프 불변성을 보존한다.

Merge-Sort 함수

이 다음은 Merge-Sort 함수이다. 전체 배열 A의 부분배열 $A[p..r]$을 또 다른 두개의 부분 배열 $A[p..q]$와 $A[q+1..r]$로 나누어 정렬하는 역할을 하며, 재귀 구조를 포함하고 있다.

Merge-Sort(A,p,r)
if p < r
    q = (p+r)//2
    Merge-Sort(A, p, q)
    Merge-Sort(A, q+1, r)
    Merge(A, p, q, r)

$p >= r$이 되는 순간, 배열에는 하나의 원소만 남으므로 굳이 정렬하지 않는다.

전체적인 병렬 정렬의 동작은 아래에 그림(Figure 1)으로 묘사되어 있다.

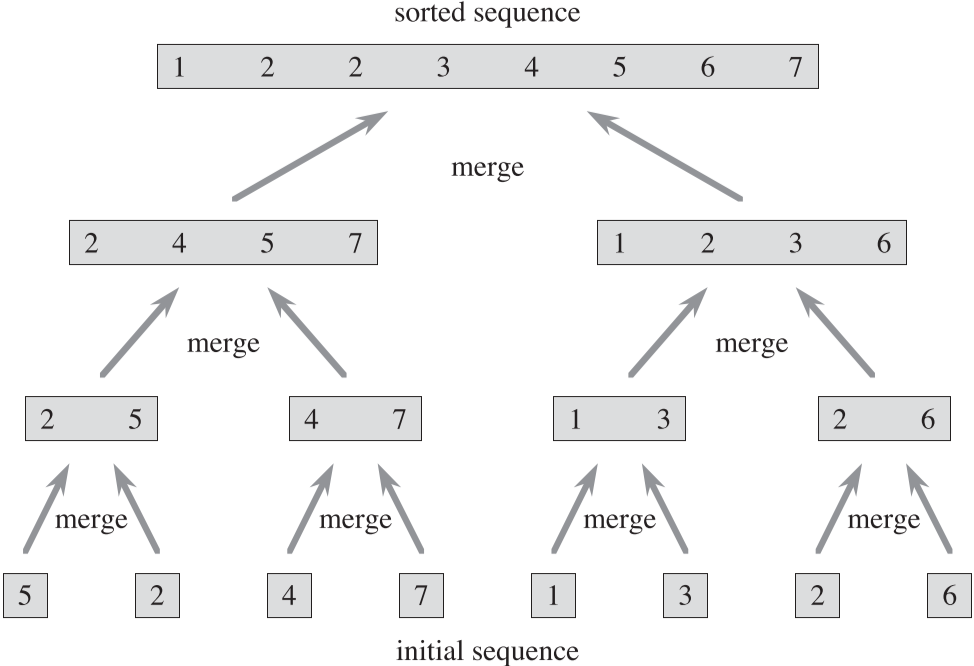
divide-and-conquer 알고리즘 분석

이러한 재귀 구조를 포함하고 있는 경우에는 점화식(recurrence equation)을 통하여 표현할 수 있다.

만약, 입력 크기 n이 어느 수준(c) 이하로 극도로 작아지면, 거의 상수 시간($O(1)$) 안에 풀린다고 볼 수 있다. 예를 들어, 배열의 원소가 하나만 있다면 정렬을 하지 않고,아래에 설명할 A 배열로 Combine 하는 시간만 존재하므로, 상수시간에 풀릴 것이다. 이때, 단 1개짜리 배열을 Combine하는데 걸리는 상수시간을 $c_1$라고 하자.

이외에는 먼저 배열을 절반으로 나누는데 $D(n)$ 만큼의 시간이 필요하고, 보통 배열의 크기와 관계없이 상수 시간이 걸린다. $D(n)=O(1)$ (Divide 과정)

절반의 배열을 정렬하는데 걸리는 시간을, 두 부분배열로 나누어 처리하므로, $2T(n/2)$만큼의 정렬 시간이 필요하다.(Conquer 과정)

마지막으로 이 둘을 위의 Merge 함수처럼 하나로 합하는데, $C(n)$ 만큼의 시간이 필요하다.(Combine 과정) 이때, 위의 Merge 함수 때 설명한 것 처럼 $O(n)$의 시간이 걸리며, 위의 1개짜리 배열을 Combined 하는데 걸리는 시간을 $c_1$이라 하였으므로, 이에 비례해 $nc_1$이라 할 수 있다.

위 경우를 식으로 정리하면 아래와 같은 점화식이 나온다.

\[T(n)=\left\{\begin{matrix} O(1),when\ n\leq c \\ D(n)+2T(n/2)+C(n) \end{matrix}\right.=\left\{\begin{matrix} c_1,when\ n = 1 \\ 2T(n/2)+nc_1 \end{matrix}\right.\]

이때 $T(n/2)$는 또한 다음과 같이 표현될 수 있다.

\[T(n/2)=\left\{\begin{matrix} O(1),when\ n\leq c \\ D(n/2)+2T(n/4)+C(n/2) \end{matrix}\right.=\left\{\begin{matrix} c_1,when\ n = 1 \\ 2T(n/4)+\frac{n}{2}\cdot c_1 \end{matrix}\right.\]

이를 대입하고, n은 1보다 크다고 가정하면 $\eqref{eq:T(n)}$ 즉, $T(n)$은 다음과 같이 정리 된다.
\(T(n)=4T(n/4)+ 2nc_1\)
이런 식으로 $T(n)$을 계속 더 작은 입력 값의 T 함수로 나누다 보면 아래 그림 Figure 2와 같은 재귀 트리 구조가 나오게 된다.

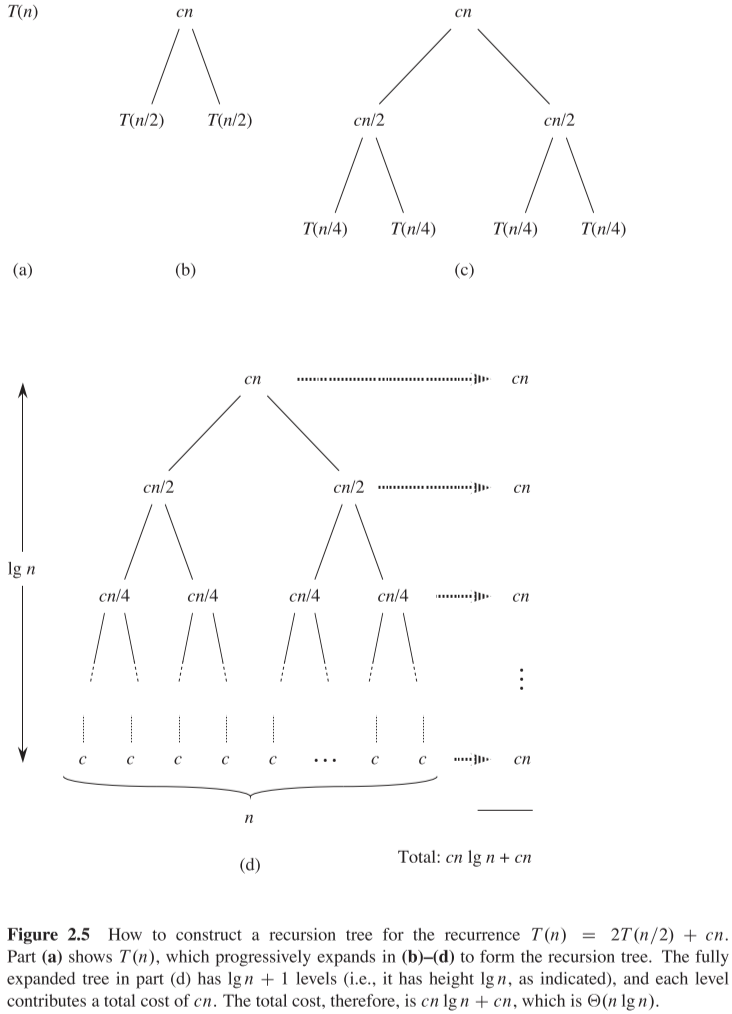
이러한 트리 구조는 상기한 그림과 같이 n의 크기가 1이 되어 상수시간이 나올 때까지 진행되는데, 이러한 층 구조는 총 $\log n + 1$ 개 만큼 생성된다. (컴퓨터 공학에서의 $\log$의 밑은 생략될 시 기본 2 임.)

그리고 각 층 구조에서 k 갈래로 생성된 비용 $cn/k$은 모두 합하면 언제나 $cn$으로 일정하므로, 각 층에서의 시간 비용은 $cn$이라고 할 수 있다.

전체 알고리즘의 시간 복잡도는 $(\log n+1)cn = cn\log n + cn$이 되며, 이를 빅오 표기법으로 나타니면 차수와 상수가 떨어지므로 최종적으로 병렬 정렬의 시간 복잡도는 $O(\log n)$이 된다.