avatar

풀스택 웹🌐 개발자 지망생 🧑🏽‍💻
➕ 인공지능 관심 🤖

Categories

Recent views

  • 1
  • 2
  • 3
  • 4
  • 5

어떻게 코딩할 것인가-함수 설계

  1. 함수 설계 과정
  2. 특수 함수 설계

함수 설계

🗣️ quote

Edx 강의 How to Code 시리즈를 정리한 내용입니다.

함수 설계 과정을 숙달하고 이해하면 어렵고 고차원의 함수를 구현할 때 큰 도움이 된다.

함수 설계는 폭포수 모델로 구현되지 않았으며 애매모호하거나 틀릴 경우 이전 단계로 돌아가서 수정해도 된다.

  • 물론 그렇다고 과정을 대충 생략하면 안된다. 각 단계는 다음 단계를 설계하는데 도움이 되게끔 설계되었다.

가끔 단계의 순번을 바꾸는 방식이 유용할 때도 있지만 4번의 구현 단계는 절대로 처음으로 오면 안된다.

  • 4번 함수 구현 자체가 이 설계의 목적이기 때문

자주, 그리고 빨리 함수를 실행시켜 조기에 잘못을 찾아 고치는게 좋다. 여러 잘못이 쌓인다면 무엇이 잘못인지 모르게 되기 때문이다.

➕ 사소한 가독성 팁

강의에서 강사님이 나는 별로 세세하게 따지지 않았었던 인덴트와 순서가 상관없는 데이터의 순서 통일 등을 통해 가독성을 올릴 수 있었다.

# data 순서가 다음과 같다면
{: #data-순서가-다음과-같다면}
data = [3, 1, 2]

# 테스트 순서도 굳이 다음과 같이 맞춰주기
{: #테스트-순서도-굳이-다음과-같이-맞춰주기}
print(fn(3)==3) 
print(fn(1)==1)
print(fn(2)==2)

함수 설계 과정

함수 디자인에 앞서 그림이나 시나리오 등을 작성하며 테스트용, 그리고 함수 내에 사용할 목적의 상수 등을 미리 정의할 수 있다.

🧾️ 함수 디자인 예시 
# 문자열의 길이가 5보다 작은지 알아보는 함수를 만들자!
{: #문자열의-길이가-5보다-작은지-알아보는-함수를-만들자}

# 1. signature, purpose, stub 설계
{: #1-signature-purpose-stub-설계}

# signature: (string => boolean)
{: #signature-string-boolean}
# purpose: 문자열을 입력받아 해당 문자열의 길이를 비교해 5보다 작은지(X) => 5 미만인지(O) 여부를 참, 거짓으로 알려주는 함수
{: #purpose-문자열을-입력받아-해당-문자열의-길이를-비교해-5보다-작은지-x-5-미만인지-o-여부를-참-거짓으로-알려주는-함수}

# stub : 테스트를 위한 임시 함수
{: #stub-테스트를-위한-임시-함수}
def isLessThan5_stub(string):
	return True
	
# 2. 테스트 설계
{: #2-테스트-설계}
print(isLessThan5_stub("") == True) # 경계값 확인
print(isLessThan5_stub("stub") == True) # True 반환 커버리지
print(isLessThan5_stub("apple") == False) # 경계 조건
print(isLessThan5_stub("computer") == False) # False 반환 커버리지


# 3. 함수 템플릿 설계
{: #3-함수-템플릿-설계}
# def isLessThan5(string):
{: #def-islessthan5-string}
# ...string 
{: #string}# ...= 무언가를 할거다는 의미

# 4. 함수 설계
{: #4-함수-설계}
def isLessThan5(string):
	return len(string) < 5

# 5. 테스트 결과 확인
{: #5-테스트-결과-확인}
print(isLessThan5("") == True) # 통과
print(isLessThan5("stub") == True) # 통과
print(isLessThan5("apple") == False) # 통과
print(isLessThan5("computer") == False) # 통과

# 만약 틀렸을 경우, 위 1~4 과정 중 애매모호하거나 잘못된 부분 확인하기
{: #만약-틀렸을-경우-위-1~4-과정-중-애매모호하거나-잘못된-부분-확인하기}

1. 시그니처, 목적, 스텁, 생성

  • 시그니처 : 인풋과 아웃풋에 대한 정보, 특히 데이터 타입,
    • 자세해야 한다. ex) Number (X) Float (O)
    • ex) 두 수 더하기 함수의 시그니처 (Integer Integer -> Integer)
      • 일부 프로그래밍 언어의 일부 함수의 경우, 리턴값이 두개 이거나 종류가 두개인 경우도 있다.
        • (Integer -> Integer or Boolean), (Integer -> Integer, name)
        • 보통 추천되지 않는다.
    • 시그니처는 설계할 함수의 모델을 결정한다.
      • 시그니처에 따라 정해진 법칙대로 함수의 템플릿과 테스트가 설계된다.
  • 목적은 해당 함수의 사용하는 목적과 입력값과 결과값의 의미
    • 단순 입력과 출력이 아니라 각각 데이터의 의미가 들어가면 좋다. 애매모호한 기준과 단어를 쓰면 안됨.
    • 다른 함수와 비교해 비슷한 일을 하는지 비교해보고, 비슷하다면 다른 함수를 이용할 수 없는지 알아보자.
🧾️ 목적의 예시

ex) 두 수가 주어지고 두 수를 더한 값이 출력 (X)

ex) 두 사람의 사과 갯수가 들어가 두 사람이 가진 사과들의 총합을 출력 (O) => 데이터의 의미

ex) 해당 수가 큰 값인지 여부를 출력 (X)

ex) 해당 수가 100보다 큰 수인지 여부를 출력 (O) => 기준이 확실

  • 스텁 : 앞으로 작성할 테스트들을 오류없이 돌려보기 위해 임시로 적당한 결과를 내놓는 함수
    • 입력값과 출력값의 데이터 타입만 맞추고 실제 값은 아무값이나 주어지면 된다.
    • 시그니처와 맞는 타입, 네이밍 컨벤션 지키기, 좋은 함수명 중요
    • ex) def add(a, b): return 0

2. 테스트 커버리지와 입력 값들을 고려한 테스트 실행 코드 작성

  • 테스트의 수는 테스트 커버리지와 각기 다른 입력값들의 구간 대표값과 경계값을 모두 고려할 수 있을 만큼 해야한다.
🧾️ 테스트 커버리지 고려 예시

첫번째 이미지가 두번째 이미지보다 길이와 너비 둘다 큰가? 함수의 경우

(너비 : 더 작은 경우, 같은 경우, 큰 경우) $\times$ (높이 : 더 작은 경우, 같은 경우, 큰 경우)가 필요하므로 경계값과 대표값을 포함해 최소 9개의 테스트가 있어야 한다.

  • 코드 커버리지: 테스트가 함수 내부의 코드의 일부를 확인하는 정도
    • 주로 분기문처럼 조건에 따라 동작하지 않을 수 있는 코드가 있는 경우, 테스트의 수를 고려해야 한다.
    • ex) (a > 3) if (a > 0) else (a < -2)의 경우, -3, -1 , 1, 4의 a값을 넣을 경우 모든 부분을 커버한다.
    • 이때 a가 가질 수 있는 각 구간의 값들 -3, -1, 1, 4를 구간 대표값이라고 한다.
  • 경계 값 또는 경계 조건 (boundary condition): 각 구간 사이 기준에 해당하거나 특수한 값(0, -1, 1) 등 성질이 바뀌는 값들을 의미
    • 주어진 두 사각형 중, 넓은 사각형을 돌려주는 함수, 그렇다면 두 넓이가 같다면?
    • 실수로 고려하지 못하는 경우가 많으며 새로 발견되면, 1번 과정도 수정해야 되는 경우가 많음
  • 테스트를 통해 함수의 목적, 필요한 상수와 데이터, 함수에 필요한 인자 등을 미리 깨달을 수 있게 하며, 이를 통해 함수 설계를 쉽게 한다.
  • 자세한 것은 테스트 설계 확인

3. 템플릿 만들기

  • 네이밍 컨벤션과 주어진 파라미터 지키기, 보통 ...(파라미터들의 나열로 표현)
  • 함수들을 구현할 때 템플릿을 복사하여 구현한다.
  • 템플릿을 완성하면 1번의 stub은 주석 처리해야 한다.
    • ex) def add(a, b): ...a ...b
  • 함수의 템플릿은 데이터 설계의 정보를 기반으로 만들면 쉽다.
🧾️ 데이터 설계와 함수 템플릿의 상관 관계

500

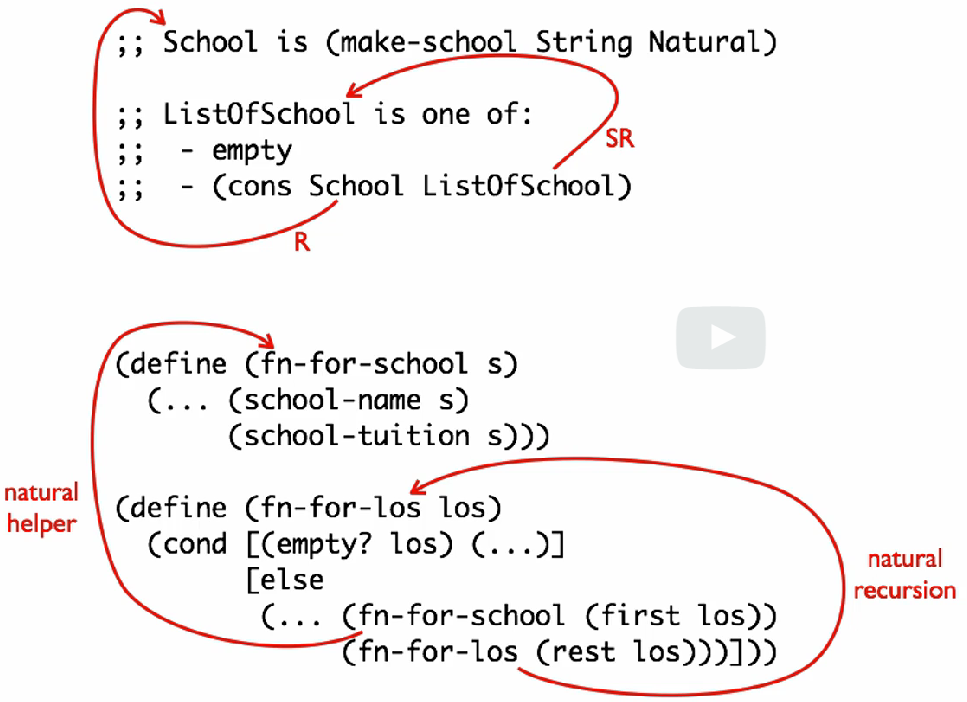
  • 보다시피 데이터 정의 과정의 참조과정을 통해 함수의 구조, 도움 함수(helper function) 등의 필요성과 위치 등을 짐작할 수 있으며, 이를 통해 함수를 쉽게 구현할 수 있다.

만약, 여러 타입의 인자가 주어진다면, 데이터 타입에 따라 템플릿을 변형해야 한다.

예를 들어, 두 개의 compound type이 인자로 주어지면 2개의 중첩된 조건문의 템플릿이 나타날 수 있다.

또한, 간단한 설명과 불변성(invariants) 테스트를 써줘야 한다.

아래 예시는 compound type의 템플릿 조건 안에 atomic distinct type의 템플릿이 추가로 결합되었다.

🧾️ 재귀구조와 empty를 가진 compound type t와 atomic distinct type k를 인자로 받는 함수 템플릿 
def lookupKey(t k):
	# k: key value to find, Integer more than 0. (invariants + interp)
	# Tests: 
	# lookupKey([], 1) == False
	# lookupKey([0, 2, 3], 1) == False
	# lookupKey([1, 2, 3], 1) == 0
	if len(t) == 0:
		# ...k
		pass
	else:
        # (...k (node-key t)    ;Integer
        #     (node-val t)    ;String
	    # lookup-key ((node-l t) (... k))
        # lookup-key ((node-r t) (... k))
        pass

4. 함수 구현하기

  • 군더더기 없이 오류없이 잘 구현하였는가?
    • 군더더기는 주로 사용하지 않는 변수, 쓸모 없는 코드, 쓸모 없는 주석을 의미
  • 보조 함수(helper function) : 함수 내부의 복잡한 로직을 추가로 구현하는 함수, 보통 데이터 정의 과정에서 들어난다.
    • 위의 데이터 설계와 함수 템플릿의 상관 관계 그림의 fn-for-school 함수 같은 함수를 의미
  • 어떻게 코딩할 것인가-추상화 와 아래 특수 함수 설계 등을 잘 참고할 것!

5. 테스트와 디버깅하기

  • 고려할 사항들
    • 모든 테스트가 예상 결과값을 통과했는가?
    • 함수 내 모든 코드들을 테스트하는가?
    • 목적에 맞는 결과를 내놓는가?
  • 만약, 오류가 생기면, 테스트가 잘못됬는지, 함수 구현이 잘못되었는지 꼭 확인하자!
  • 빠르게, 자주 테스트하여 잘못을 조기에 발견하자!

함수 완성 이후

  • 함수의 설명 부분을 다시 작성해보자. 여러 로직이 겹치는 경우 보조함수로 바꿔야 한다.
  • 시그니처와 스텁은 더이상 의미없으므로 지우거나 옮기자.
  • 테스트는 경우에 따라 재활용하거나 후에 디버깅 원인 분선시 필요할 수 있으므로 옮기거나 잘 정리하자
  • 리팩토링 및 캡슐화 고려

특수 함수 설계

함수 내부에 또 다른 함수를 포함한 함수를 설계하기 위한 방법 소개

재귀 함수 설계

자기 자신 함수를 함수 로직 내에 이용하는 함수

✍ 재귀 함수 구현 시 유의점
  • 데이터 설계 시 재귀 구조가 나타난다면, 함수 구현 시에도 재귀 구조가 나타난다.
  • 기필코 기저 사례(Base Case)가 존재해야 하며, 도달 가능해야 한다.
    • 그렇지 않으면 무한 루프가 일어난다.
  • 로직 구현시, 테스트 생성 및 구현 시 기저 사례를 맨 처음 처리할 것.
    • 구현이 간단한 경우가 많고, 재귀 함수 구현을 위해 꼭 필요하므로 빠르게 디버깅 하기 위함
  • 재귀 사례는 결국 기저 사례로 향하는지 알기 위해, 내부 재귀함수의 인자가 기저 사례로 수렴하도록 변경되는지 확인해야 함.
  • 재귀 함수의 결과값이 항상 특정 조건을 만족한다는 가정을 충족해야 한다.(Invariant) 아래 예시 참조
  • 보조 함수와 다르게 새로 테스트를 작성할 필요가 없다.
🧾️ 재귀 함수와 재귀 데이터 설계 예시 : 짝수 필터링

사실, 많은 경우 재귀로 처리하는 것보다 반복문으로 처리하는 경우가 성능 상으로 좋은 경우가 많다.

# Data definition:
{: #data-definition}

# ListOfNumber is one of the
{: #listofnumber-is-one-of-the}
# - empty
{: #empty}
# - [Integer] + ListOfNumber 
{: #integer-listofnumber}# 데이터 설계 중 재귀 구조 발견
# interp. an arbitrary number of Numbers
{: #interp-an-arbitrary-number-of-numbers}

def fnForLon(lon):
	if len(lon)==0:
		#...
		pass
	else:
		#...lon[0]
		#...fnForLon(lon[1:])
		pass

# Function:
{: #function}
# ListOfNumber -> ListOfNumber
{: #listofnumber-listofnumber}
# filter even Number from ListOfNumber.
{: #filter-even-number-from-listofnumber}
# Invariants : All the results of evenFilter should contain only odd number.
{: #invariants-all-the-results-of-evenfilter-should-contain-only-odd-number}
# Stub
{: #stub}
# def evenFilter(lon):
{: #def-evenfilter-lon}
#	return []
	
print(evenFilter([0])==[])
print(evenFilter([4,3,2,1])==[3, 1])

# <Template From fnForLon>
{: #template-from-fnforlon}

def evenFilter(lon):
	if len(lon)==0:
		return []
	else:
		return ([lon[0]] if lon[0]%2 else []) + evenFilter(lon[1:]) # 이후 evenFilter는 모두 홀수만 포함된다는 가정을 충족해야 한다. (Invariant)

불변성(Invariants)

복합 함수의 경우 어떤 함수의 결과물이 항상 특정 조건을 만족한다는 가정이 충족해야 할 필요가 있다.
이를 불변성이라고 하며, 이를 엄격히 지키는지 확인하기 위해 로직을 수학적으로 증명하고, 테스트를 세세하게 짜내어야 한다.
불변성이 깨지면 가정이 깨지므로 원하는 결과가 나오지 않는다.
불변성은 재귀나 복합 함수 뿐만 아니라 반복문의 반복 과정에서도 사용된다.

예시로 동적 계획법의 점화식이나 이중 탐색 트리의 좌측 자식은 언제나 현재 노드의 값보다 작고, 우측 자식은 언제나 현재 노드의 값보다 큼 등이 있다.

생성적 재귀(Generative Recursion)

앞서 소개했던 함수들은 구조적 재귀(Structural Recursion)로, 이미 주어진 특정 데이터(배열, 링크드 리스트 등)을 순회하며 진행하는 재귀로, 이미 구조가 정해져있고, 데이터를 전부 순회하는 순간으로 재귀의 종료가 명확히 정해져있다.

생성적 재귀는 재귀 함수 중에 데이터를 추가로 생성하는 구조로, 구조 예측이 힘들고, 재귀의 종료가 보장되지 않는다.

또한, 데이터 설계 과정에 재귀 구조임을 암시하는 부분이 나오지 않는다.

🧾️ 생성적 재귀 구조 함수 설계 예시 : 프랙탈 
(define CUTOFF 2)

;; Number -> Image
;; produce a Sierpinski Triangle of the given size
(check-expect (stri CUTOFF) (triangle CUTOFF "outline" "red"))
(check-expect (stri (* CUTOFF 2))
              (overlay (triangle (* CUTOFF 2) "outline" "red")
                       (local [(define sub (triangle CUTOFF "outline" "red"))]
                         (above sub
                                (beside sub sub))
                       )))

; (define (stri s) (square 0 "solid" "white")) ; stub

#;
(define (genrec-fn d)
  (if (trival? d)
      (trival-answer d)
      (... d
           (genrec-fn (next-problem d)))))

(define (stri s)
  (if (<= s CUTOFF)
      (triangle s "outline" "red")
      (overlay (traingle s "outline" "red")
               (local [(define sub (stri (/ s 2)))]
                 (above sub
                        (beside sub sub))))))

따라서 생성적 재귀는 정교한 기반사례(Base case) 설계와 기반 사례로 수렴한다는 증명이 필요하며, 이는 아래와 같은 종료 논의를 통해 고민해볼 수 있다.

✍ 종료 논의(termination argument) 예시

예를 들어 다음과 같은 재귀 함수의 종료 논의는 다음과 같다.

def recur(s):
	if s < 1:
		print(s)
		return
	recur(s/2)

기반 사례(Base Case): 언제 재귀를 멈추는가?

주로, 조건식, 예시의 s < 1

감소 단계(Reduction step): 다음 재귀에 넘겨지는 인자의 변화

주로 재귀 함수에 주어지는 인자, 예시의 s/2

감소 단계의 인자의 변화가 기반 사례에 결국 언젠가 기반 사례에 다다른다는 증명(Argument that repeated application of reduction step will eventually reach the base case): 감소 단계의 연속이 결국 기반 사례로 향하는가?

예시에서는 값 s는 감소 단계 s/2로 값이 절반이 되다보면 결국엔 기반사례 조건 s<1에 도달하게 됨.

축적자(Accumulator)

재귀 함수 중에 재귀 과정 자체에 대한 정보를 가지고 있는 변수이다.

재귀 함수는 같은 함수여도 재귀로 불러오게 되면, 인자로 넘겨받은 변수 이외에는 초기화되므로, 이를 이용해 재귀가 진행되면서 정보를 유지할 수 있다.

🧾️ 축적자 예시와 추가 단계

축적자 추가는 아래 예시에 적힌 총 7 단계로 진행된다.

함수 템플릿 변형을 응용해 축적자를 추가하고, 불변성과 설명에 맞게 템플릿을 변형 및 구현하는 것이다.

; PROBLEM:
; 
; Design a function that consumes a list of elements and produces the list
; consisting of only the 1st, 3rd, 5th and so on elements of its input. 
; 
;    (skip1 (list "a" "b" "c" "d")) should produce (list "a" "c")
; 
;; (listof X) -> (listof X)
;; produce list consisting on only the 1st, 3rd, 5th... elements of lox
(check-expect (skip1 empty) empty)
(check-expect (skip1 (list "a" "b" "c" "d")) (list "a" "c"))
(check-expect (skip1 (list 1 2 3 4 5 6)) (list 1 3 5)) 

;(define (skip1 lox) empty);stub
#;
(define (skip1 lox)
  (cond [(empty? lox) empty]
        [else
         (if (odd? POSITION-OF-FIRST-LOX) 
         # 단계1: 축적자가 필요함을 인식하고 해당 부분을 표시해둔다 (대문자 POSITION-OF-FIRST-LOX)
             (cons (first lox)
                   (skip1 (rest lox)))
             (skip1 (rest lox)))])) 

# 단계 2: 함수 시그니처에 축적자를 추가한다.
{: #단계-2-함수-시그니처에-축적자를-추가한다}
(define (skip1 lox acc)  
	# 단계 3: 함수 시그니처에 대한 설명과 불변성(invariants)를 설명하고 재귀 함수 진행시 변화를 명시한다.
	;; acc: Natural; 1-based position of (first lox) in lox0
	;; first: (skip1 (list "a" "b" "c") 1)
	;; next:  (skip1 (list      "b" "c") 2)
	;; next:  (skip1 (list          "c") 3)

  (local [(define (skip1 lox acc)) 
  # 단계 3: 축적자가 포함되어있는 내부 함수로 템플릿을 감싼다.
          (cond [(empty? lox) empty] 
          # 단계 4: 함수 템플릿을 추가 인자로 변형 한다. 여기서는, (...acc)를 각 분기마다 추가.
                [else
                 (if (odd? acc) 
                 # 단계 5 : 기존에 축적자 표시한 부분과 재귀 함수 호출 부분에 축적자를 추가한다.
                     (cons (first lox)
                           (skip1 (rest lox) (add1 acc)))
                     (skip1 (rest lox) (add1 acc)))])]
    (skip1 lox0 1)))  
    # 단계 6: 축적자의 초기값을 설정한다.
# 단계 7: 결과를 테스트 해본다.
{: #단계-7-결과를-테스트-해본다}

축적자를 만들기 위한 함수 템플릿은 모두 동일하지 않지만, 축적자를 추가하며, 함수의 템플릿을 변경하는 부분에 신경쓰자

용도에 따라 크게 세가지 축적자가 존재한다.

  • 문맥보존 축적자(Context-preserving Accumulator)
    재귀함수 간에 보존되어야 할 정보를 담는 축적자
    ex) 트리 내부에서 특정 값을 찾는 재귀 함수에서 “특정값” 축적자
  • 현재결과 축적자(result-so-far Accumulator)
    재귀함수가 진행되며 변화된 값을 담은 축적자
    ex) 트리 내부 값들의 총 합을 구하는 재귀 함수에서 지금까지 더한 값 축적자
  • 작업명단 축적자(worklist Accumulator)
    남은 재귀함수를 진행하기 위한 리스트를 담은 축적자
    ex) BFS 탐색 재귀함수에서 큐에 들어간 노드 리스트 축적자

이중에 두번째와 세번째, 현재결과 축적자와 작업명단 축적자는 꼬리 재귀함수(Tail recursive function)을 구현하는데 사용할 수 있다.
예를 들어, 재귀함수의 결과에 덧셈 연산을 하지 않고 현재결과 축적자 인자에 대신 덧셈을 하거나, 여러 재귀 함수를 결과값에 부르지 않고, 작업명단 축적자에 추가하여 차례대로 처리하게 하는 것이다.

보조 함수 설계

보조 함수(helper function)는 자기 자신이 아닌 다른 함수로, 복잡한 함수의 일부 로직을 담당하는 함수이다.

다음과 같은 경우에 보조 함수를 설계해야 한다.

  • 함수 설계 중 설계 내용이 새로운 지식 도메인으로 바뀜(즉, 두가지 이상의 일을 함)
  • 데이터 설계 중 참조가 발견됨
  • 함수 해석 부분 구현 시, 내용이 길고 복잡함
⚠️ 의미없는 보조함수의 추가는 오히려 구현을 복잡하게 만들 수 있다.

보조 함수 설계시, 각 보조 함수의 기능과 데이터를 따로 설계하고, 테스트 해야 함.

  • 이때, 복잡한 구조일 수록 내부의 보조 함수를 염두에 두고 최대한의 커버지리가 가능한 테스트를 설계해야 한다.
  • 하지만, 반대로 보조 함수는 자신을 참조하는 부모 함수를 염두에 두지 않고 자신의 기능만 신경쓰면 된다.

보조 함수는 자신을 위한 또 다른 보조 함수를 가질 수 있다.

🧾️ 보조 함수 의존 관계

아래 그림처럼 특정 함수의 테스트와 설계의 끝은 해당 함수 내부에서 의존하는 보조 함수들의 설계와 테스트가 전부 끝나야 가능하다.

500

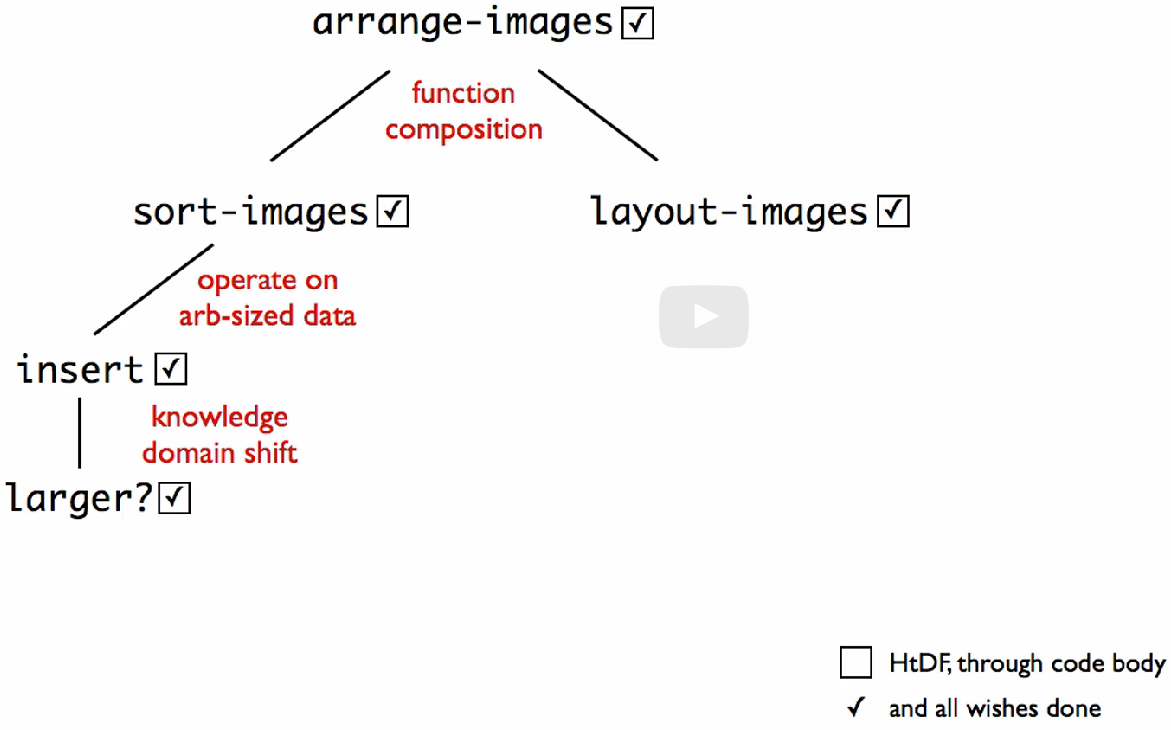
따라서, 각 보조 함수를 일단 위시리스트 항목으로 만들어 두고 상위 함수를 먼저 구현할 수 있다.

➕ 위시리스트 항목(wish-list entry)?

시그니처, 목적, !!!와 스텁으로 이루어진 완성되지 못한 함수

스텁과 다른 점은 처음에는 스텁처럼 생겼지만 언젠가는 추가로 테스트와 내부 로직을 제대로 구현한다는 점이다.

!!!, TODO:등을 통해 나중에 꼭 구현하도록 표시해둔다.

# Number -> Number
{: #number-number}
# 고양이를 우측으로 1 픽셀 옮긴 좌표를 출력
{: #고양이를-우측으로-1-픽셀-옮긴-좌표를-출력}
# !!! or TODO:
{: #or-todo}
def advanceCat(c):
	return 0
🧾️ 구현 완료된 위시 리스트 항목 
# 구현 완료된 위시 리스트 항목
{: #구현-완료된-위시-리스트-항목}
# CAT -> CAT
{: #cat-cat}
# produce the next cat, by advancing it 1 pixel to right
{: #produce-the-next-cat-by-advancing-it-1-pixel-to-right}
# Tests:
{: #tests}
print(advanceCat(3)==4)

# def advanceCat(c): return 1 
{: #def-advancecat-c-return-1}# stub

# <use template from Cat>
{: #use-template-from-cat}
def advanceCat(c):
	return c+1

# CAT -> Image
{: #cat-image}
# render the cat image at appropriate place on MTS
{: #render-the-cat-image-at-appropriate-place-on-mts}
print(render(4)==Image("cat", 4, CTR_Y, MTS))

# def render(c): return MTS 
{: #def-render-c-return-mts}# stub
# <use template from Cat>
{: #use-template-from-cat}
def render(c):
	return Image("cat", c, CTR_Y, MTS)

상호 참조 함수 설계

상호 참조 함수는 보조 함수와 비슷하게 특정 기능을 다른 함수의 참조로 해결한다.

보조 함수와 다른 점은, 다른 함수 또한 자신의 함수를 포함하는 상호 참조 관계를 가진 함수라는 점이다.

  • 정확히는 둘 이상의 함수가 사이클을 이룰 수도 있다.

상호 참조 데이터 설계 시와 비슷하게, 함수 설계시 서로의 로직이 서로 영향 받으므로, 상호 참조 함수들을 모두 동시에 함께 설계를 진행한다.

🧾️ 상호 참조 함수 설계 예시 : 트리 내 이름 검색 
# Data definitions:
{: #data-definitions}
# Element is (make-elt String Integer ListOfElement)
{: #element-is-make-elt-string-integer-listofelement}
# interp. An element in the file system, with name, and EITHER data or subs.
{: #interp-an-element-in-the-file-system-with-name-and-either-data-or-subs}
#         If data is 0, then subs is considered to be list of sub elements.
{: #if-data-is-0-then-subs-is-considered-to-be-list-of-sub-elements}
#         If data is not 0, then subs is ignored.
{: #if-data-is-not-0-then-subs-is-ignored}

# ListOfElement is one of:
{: #listofelement-is-one-of}
#  - empty
{: #empty}
#  - [Element] ListOfElement
{: #element-listofelement}
# interp. A list of file system Elements
{: #interp-a-list-of-file-system-elements}

def fnForElt(name, data, loe): # Compound data
	# ... (name) :String
	# (data) : Integer
	# fnForLoe(loe) : Reference
	pass


def fnForLoe(loe):
	if len(loe)==0:
		#...
		pass
	else:
		#...loe[0]
		#...fnForLoe(loe[1:])
		pass

F1 = {name: "F1", data: 1, subs: []}
F2 = {name: "F2", data: 2, subs: []}
F3 = {name: "F3", data: 3, subs: []}
D4 = {name: "D4", data: 0, subs: [F1, F2]}
D5 = {name: "D5", data: 0, subs: [F3]}
D6 = {name: "D6", data: 0, subs: [D4, D5]}


# Search the given tree for an element with the given name, produce data if found; false otherwise
{: #search-the-given-tree-for-an-element-with-the-given-name-produce-data-if-found-false-otherwise}
# String Element -> Integer or false
{: #string-element-integer-or-false}
# String ListOfElement -> Integer or false
{: #string-listofelement-integer-or-false}

print(findLoe("F3", [])==False)
print(findElement("F3", [F1])==False)
print(findElement("F3", [F3])==3)
print(findElement("D4", [D4])==0)
print(findElement("D4", [D4])==0)
print(findLoe("F2", [F1, F2])==2)
print(findLoe("F3", [F1, F2])==False)
print(findElement("F3", [D4])==False)
print(findElement("F1", [D4])==1)
print(findElement("F2", [D4])==2)
print(findElement("F3", [D6])==3)

# def findElement(n, e): 
{: #def-findelement-n-e}
#     return False 
{: #return-false}#stubs

# def findLoe(n, loe):
{: #def-findloe-n-loe}
#     return False 
{: #return-false}#stubs

# <Template from Element>
{: #template-from-element}
def findElement(n, e):
	if e.name == n:
       return e.data
    return findLoe(n, e.subs)
    
# <Template from ListOfElement>
{: #template-from-listofelement}
def findLoe(n, loe):
	if len(loe)==0:
		return False
	else:
        if findElement(n, loe[0]) != False:
             return findElement(n, loe[0])
	    return findLoe(n, loe[1:])

여러 경우의 수를 가진 데이터를 다수 포함한 복합 데이터 함수 설계

데이터 설계 단계

관건은 데이터 설계 단계에서 각 데이터의 경우의 수(one-of)를 잘 찾아 설계해야 한다.

테스트 단계

간혹, 함수 중에 입력 받는 두개의 데이터들이 여러 개의 경우의 수를 갖는 경우가 있다.
이럴 경우 각 경우의 수를 가진 표를 그리면 쉽게 함수를 설계할 수 있다.

🧾️ 표를 이용한 함수 설계

예시 : 두 개의 배열을 입력받는 복합 데이터 함수
두 개의 문자열 A, B를 받아 A가 B의 접두어인지의 여부를 알려주는 함수

  문자열 A 길이 0 문자열 A 길이 1 이상
문자열 B 길이 0 true false
문자열 B 길이 1 이상 true 접두어 비교 필요

각 문자열 A, B의 경우의 수는 2개이며, 표를 그려본 결과, 따라서 최소 $2\times2=4$개의 테스트가 필요하다는 것을 알 수 있다.

만약, 데이터의 수가 늘어난다면 표의 차원의 수가 늘어나며, 각 경우의 수가 늘어난면, 각 차원의 크기가 늘어나야 한다.

함수 설계 단계

함수 설계 시, 주로 SWITCH 문이나 If-Else 문을 통해 구현하게 되는데, 이때 함수의 ABC Size 를 줄이기 위해 표(=모델)을 잘 살펴보고 간략화 해야한다.

🧾️ 표를 이용한 함수 설계-모델 간략화

예시 : 두 개의 배열을 입력받는 복합 데이터 함수
두 개의 문자열 A, B를 받아 A가 B의 접두어인지의 여부를 알려주는 함수

  문자열 A 길이 0 문자열 A 길이 1 이상
문자열 B 길이 0 true false
문자열 B 길이 1 이상 true 접두어 비교 필요

앞서 표에서 4개의 테스트를 작성했지만, 실제 필요한 경우의 수는 다음 사진과 같이 3개이다.

문자열 A는 길이가 0일 경우 언제나 참을 반환하므로, 문자열 B가 비어있던 말던 하나의 경우의 수로 볼 수 있다.

따라서 경우의 수 두개를 하나로 합칠 수 있다.

  • 이런 식으로 합쳐진 커다란 크기의 경우의 수 먼저 처리하며 함수를 설계하면 수월하다.

이러한 방법을 모델 단계에서 함수를 간략화한다고 하여 모델 간략화라고 한다.

간략화를 안한 함수 모델과 간략화한 뒤의 함수 모델을 비교해보자.

def noSimpleIsPrefix(A, B):
	if len(A) == 0 and len(B) == 0:
		return True
	elif len(A) == 0 and len(B) != 0:
		return True
	elif len(A) != 0 and len(B) == 0:
		return False
	elif len(A) != 0 and len(B) != 0:
		# ...A[0],A[1:],B[0],B[1:]
		pass

def SimpleIsPrefix(A, B):
	if len(A) == 0: # 2개의 경우의 수 하나로 합친 것 먼저 처리
		return True
	elif len(B) == 0: # len(A) != 0 임이 보장되므로 확인할 필요 없음.
		return False
	else:
		# ...A[0],A[1:],B[0],B[1:] 
		# 엄밀히 말하면 배열을 위한 함수 템플릿(재귀 템플릿)
		pass

모델 간략화쪽이 더 가독성이 좋고, 코드가 짧으며 경우의 수가 적음을 알 수 있다.

🧾️ 더 어려운 모델 간략화 코드(BSL) 
;; ==========
;; Functions:

;; Pattern ListOf1String -> Boolean
;; produces true if ListOf1String matches the given pattern

; CROSS PRODUCT OF TYPE COMMENTS TABLE  
; 
;                                      LO1s
;                             empty        (cons 1String ListOf1String) 
; 
; P   empty                   true          true                       
; a
; t  (cons "A" Pattern)       false        (and (alpha? (first los))
; t                                             (match-head? <rests>)) 
; e
; r  (cons "N" Pattern)       false        (and (numer? (first los)) 
; n                                             (match-head? <rests>))
; 


(check-expect (pattern-match? empty empty) true)
(check-expect (pattern-match? empty (list "a")) true)
(check-expect (pattern-match? (list "A") empty) false)
(check-expect (pattern-match? (list "N") empty) false)
(check-expect (pattern-match? (list "A" "N" "A") (list "x" "3" "y")) true)
(check-expect (pattern-match? (list "A" "N" "A") (list "1" "3" "y")) false)
(check-expect (pattern-match? (list "N" "A" "N") (list "1" "a" "4")) true)
(check-expect (pattern-match? (list "N" "A" "N") (list "1" "b" "c")) false)
(check-expect (pattern-match? (list "A" "N" "A" "N" "A" "N")
                              (list "V" "6" "T" "1" "Z" "4")) true)

; template taken from cross product table
; 6 cases simplifed to 4

(define (pattern-match? pat lo1s)
  (cond [(empty? pat) true]                            
        [(empty? lo1s) false]                          
        [(string=? (first pat) "A")                    
         (and (alphabetic? (first lo1s))
              (pattern-match? (rest pat) (rest lo1s)))]
        [(string=? (first pat) "N")                    
         (and (numeric? (first lo1s))
              (pattern-match? (rest pat) (rest lo1s)))]))

;; 1String -> Boolean
;; produce true if 1s is alphabetic/numeric
(check-expect (alphabetic? " ") false)
(check-expect (alphabetic? "1") false)
(check-expect (alphabetic? "a") true)
(check-expect (numeric? " ") false)
(check-expect (numeric? "1") true)
(check-expect (numeric? "a") false)

(define (alphabetic? 1s) (char-alphabetic? (string-ref 1s 0)))
(define (numeric?    1s) (char-numeric?    (string-ref 1s 0)))