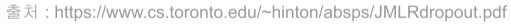정형 데이터 분류 기본

Dec 14, 2022

1. 정형 데이터와 데이터의 이해
2. EDA
3. 데이터 전처리(Preprocessing)
   • 연속형, 범주형 처리
   • 결측치 처리
   • 이상치 처리
4. 머신 러닝 개념
   • Underfitting & Overfitting
   • Validation strategy
   • Reproducibility(재연성)
   • Machine learning workflow
5. 트리 모델 소개
   • What is tree model
   • Tree model with hyper-parameter

정형 데이터 분류 기본

Naver AI Boostcamp의 정형 데이터 분류 강의를 정리한 내용입니다.

정형 데이터와 데이터의 이해

정형 데이터란, 엑셀 파일이나 관계형 데이터베이스의 테이블에 담을 수 있는 데이터로 행(row)과 열(column)으로 표현 가능한 데이터. 하나의 행은 하나의 데이터 인스턴스를 나타내고, 각 열은 데이터의 피처를 나타냄

비정형 데이터란 이미지, 비디오, 음성, 자연어 등의 정제되지 않은 데이터

정형 데이터는 범용적인 데이터이며, 가장 기본적이 데이터로 필수적이다.

정형 데이터의 분석을 위해서 문제를 이해해야 하며, 어떻게 문제를 풀지 고민해야 한다.

• 예를 들어 Input 데이터를 Aggregation 형태로 넣어주거나, TimeSeries로 넣어주거나, 양쪽 둘다 넣어주기
  • Aggregation: ex) 사람 하나당 하나의 row를 가지는 형식

• Train, Valid, Test 셋 나누기

• 적절한 평가지표를 선정해야 함.

분류(Classification) : 예측해야할 대상의 개수가 정해져 있는 문제 (ex) 신용카드 정상 거래 분류)

회귀(Regression) : 예측해야할 대상이 연속적인 숫자인 문제 (ex) 일기 예보 기온 예측)

평가지표(Evaluation Metric) : 분류, 회귀 머신러닝 문제의 성능을 평가할 지표

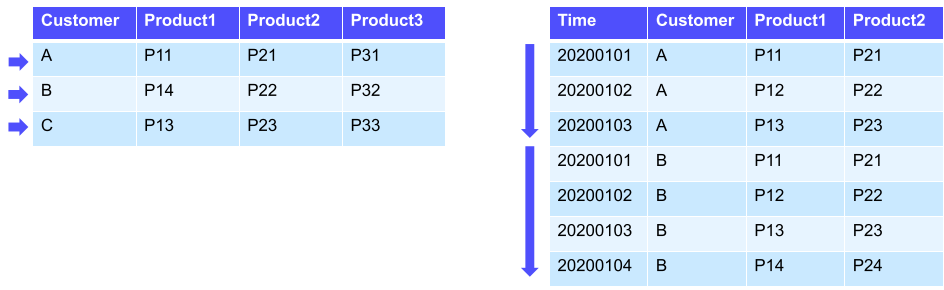
분류 문제의 평가지표를 알기 위해서 예측 경우를 정의한 Confusion Matrix에 대해서 알아야 한다.

TN : False를 False로 예측

FP : False를 True로 예측

FN: True를 False로 예측

TP: True를 True로 예측

분류 문제의 평가 지표들

1. Accuracy (정확도): (TP + TN)/(TP+TN+FP+FN)

• 전체 비율 중 올바르게 분류한 비율
• 불균형 데이터에는 비적합함.
  • 100명 환자 중 1명의 암환자를 찾는 데이터에서 전부 그냥 환자가 아니라고 해도 99%의 정확도를 가진다.

1. Precision(정밀도): TP / (TP + FP)

• 모델이 True로 예측한 값 중 실제 True인 경우의 비율
• Negetive 데이터가 중요한 경우 사용
  • 스팸 메일 분류(일반 메일은 스팸 메일로 분류해서 삭제하면 큰일남)

1. Recall(재현율) : TP / (TP + FN)

• 실제 값이 True인 값 중 모델이 True라고 한 경우의 비율

• Positive 데이터가 중요한 경우 사용

  • 종양의 종류 판단 시, 양성 종양이냐 악성 종양이나 분류

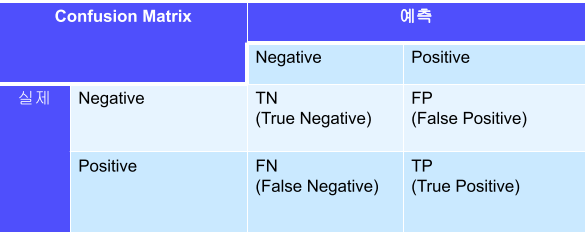
ROC(Receiver operating characteristics, 수신자 조작 특성)

• TPR(True Positive Ratio)$=\frac{TP}{TP+FN}$을 Y축, FPR(False Positive Ratio)$=\frac{FP}{FP+TN}$을 X축으로 하여 모델의 임계값을 바꿔가면서 그린 곡선

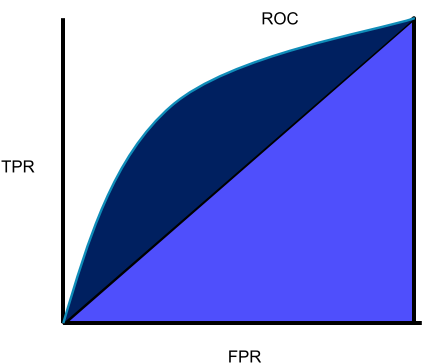
AUC(Area Under Curve)

ROC의 면적을 표시한 것, 0과 1사이의 값을 가짐,

1일수록 성능이 좋음.

EDA

EDA(Exploratory Data Analysis, 탐색적 데이터 분석)

데이터를 탐색하고 가설을 세우고 증명하는 과정, 주어진 문제를 데이터를 통해 해결하기 위해 필요하다.

때문에 적절한 전처리, 방법론들을 선택하고, 가설과 의문을 세운뒤 검증, 입증하여 해결한다.

EDA의 과정

1. Data에 대한 가설 혹은 의문
2. 시각화 혹은 통계량, 모델링을 통한 가설 검정
3. 위의 결론을 통해 다시 새로운 가설 혹은 문제 해결

데이터 종류, 도메인, 사용 모델 등에 따라 EDA의 방향성과 방법이 달라지며, 정해진 답이 존재하지 않음

때문에 EDA 과정에서 수많은 활동과 과정을 거쳐야 하며, 이를 방향성 없이 풀어나가는 것은 비효율적이므로, 다음 두가지를 기본 개요로 놓고 시작한다.

1. 개발 변수의 분포(Variation)

2. 변수 간의 분포와 관계(Covariation)

Titanic data를 이용한 EDA의 예시

이름, 성별, 나이, 좌석 등을 이용해 생존 여부를 판단하는 Task

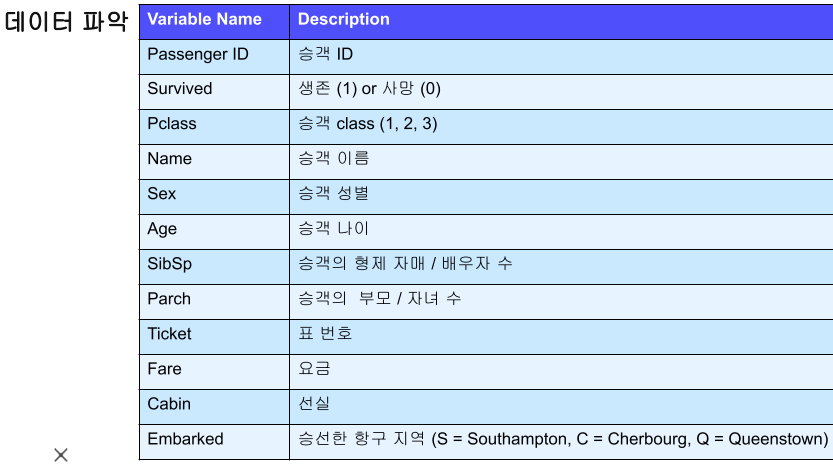
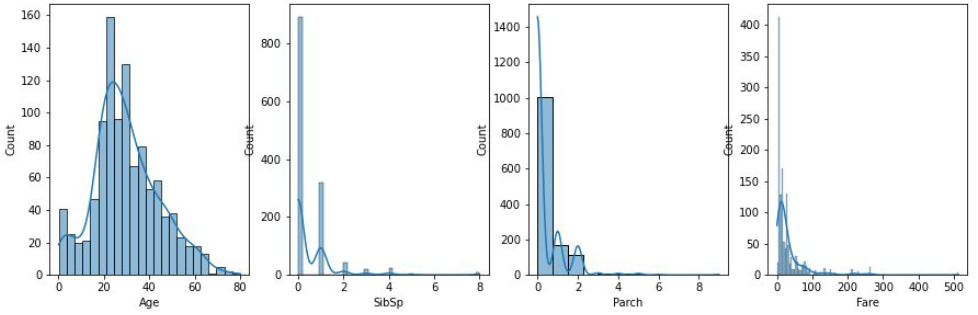
Age, SibSp, Parch, Fare 등은 연속형 변수이며, Age의 경우 포아송 분포를 따르고 있다.

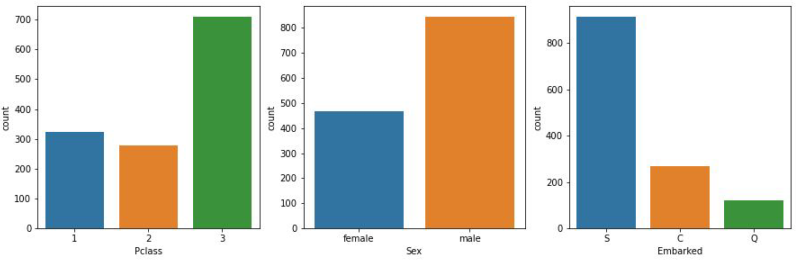
Pclass, sex, Embarked 등은 각 값이 구분 이외에는 의미가 없는 범주형이며, 상식적으로 female과 male은 동일해야하고, Pclass의 경우 높은 등급이 더적어야 하므로, 데이터 불균형이나 특별한 상황을 가정할 수 있다.

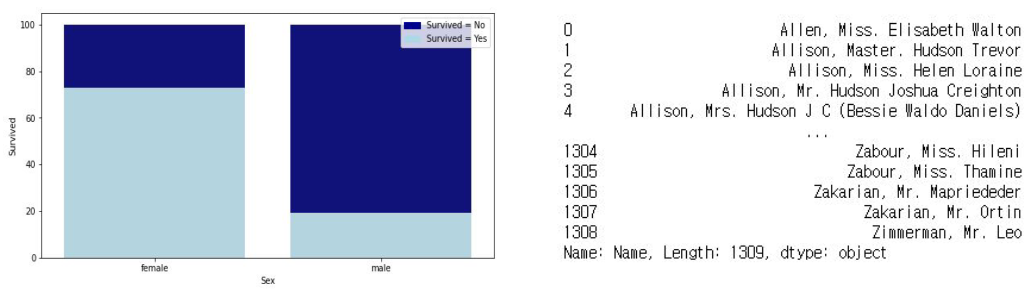
변수 간 그래프를 통해 변수의 관계를 알 수 있다. 위의 경우 당시 타이타닉에서 여성이 남성보다 생존하도록 배려를 받았음을 알 수 있다.

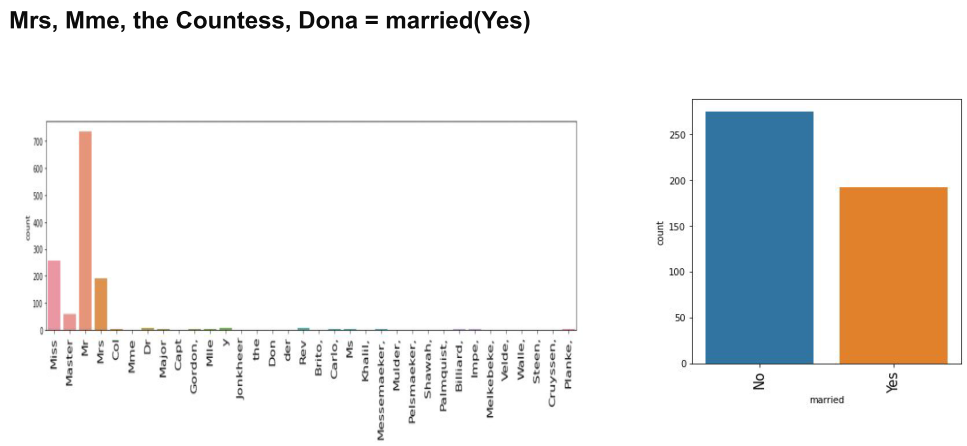
기존 변수에서 다른 변수를 추출해서 변수간의 관계를 비교할 수 도 있다.

위의 경우 이름에서 결혼 여부를 추출하여 생존여부를 따져 보자 미혼 여성이 생존자가 많다는 것을 알 수 있다.

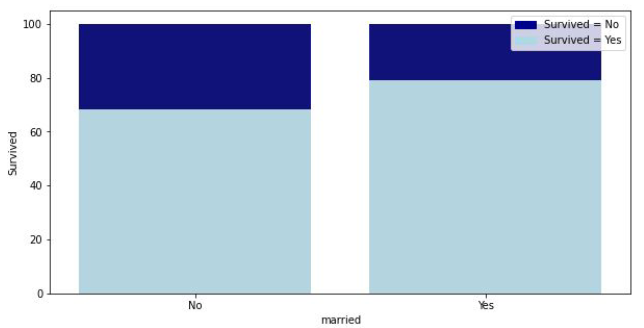
하지만 생존비율은 결혼한 여성이 더욱 많이 살아남았다.

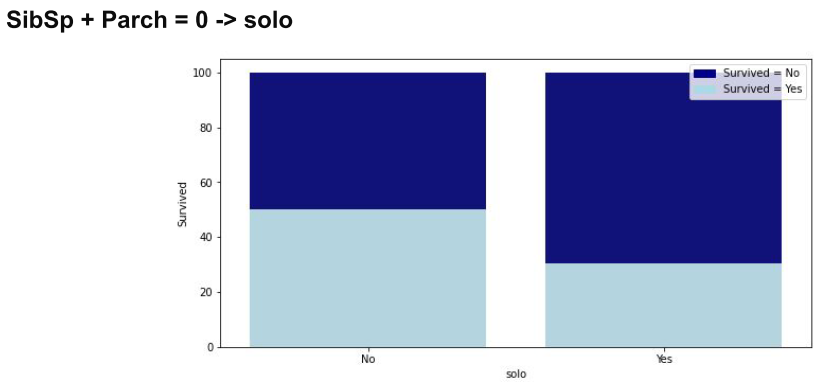
또한 기존의 변수 여러개를 이용해 새로운 변수 또한 만들 수 있다.

혼자 탑승한 사람은 생존율이 좀더 낮다.

데이터 전처리(Preprocessing)

데이터 전처리는 머신러닝 모델에 데이터를 입력하기 위해 데이터를 처리하는 과정

EDA, 모델, 목적에 따라 방법이 달라지게 된다.

연속형, 범주형 처리

연속형 데이터 처리

Scaling 방법

데이터의 단위 혹은 분포를 변경하는 방법, 선형기반의 모델(선형회귀, 딥러닝 등)인 경우 변수들 간의 스케일을 맞추는 것이 필수적

1) Scaling만 하기
$$
\left{\begin{matrix}\begin{alignat*}{0}

1. Min\ Max\ Scaling\ :\mathbf{X}_{new}=\frac{\mathbf{X}_i-\min(\mathbf{X})}{\max(\mathbf{X})-\min(\mathbf{X})}\
2. Standard\ Scaling:X_{new}=\frac{x-\mu}{\sigma}\
3. Robust\ Scaling:X_{scale}=\frac{x_i-x_{med}}{x_{75}-x_{25}}
   \end{alignat*}\end{matrix}\right.
   $$
   Scaling에는 다양한 방법이 존재하며, 대표적으로

• Min Max Scaling

현재 값에 최소값을 뺀 뒤, 최대값과 최소값으로 나눔

• Standard Scaling

현재 값을 평균으로 빼고, 표준편차로 나눔

• Robust Scaling : 이상치에 영향을 가장 덜 받음

현재 값을 중위 값으로 빼고 IQR(이상치 부분 참조)로 나눠서 계산

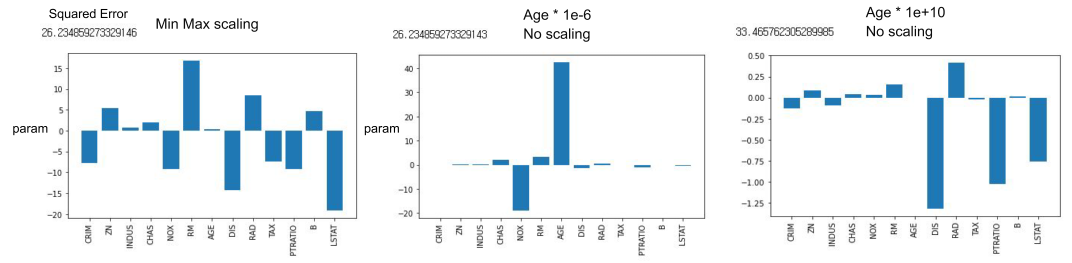
스케일에 따라 계수 값에 따른 모델의 해석과 모델 성능에 영향이 간다.

2) Scaling + Distribution(분포 변경) + Binning 하기

1. Log transformation

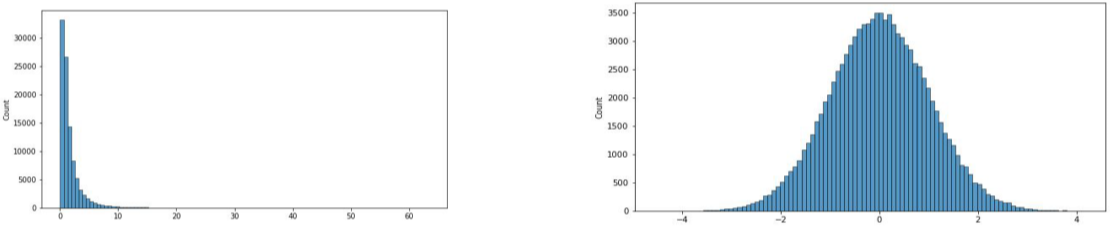
변수의 분포가 치우친 경우, Log Transformation으로 정규분포와 비스무리하게 바꿔줄 수 있음

exponential Transformation의 경우 정반대의 결과를 냄

1. Quantile transformation

어떤 분포가 나와도 Uniform(모두 동일한 높이의 그래프), 또는 정규 분포로 바꿔줌

값을 나열한 뒤, 값의 분위 수에 따라 변환해줌

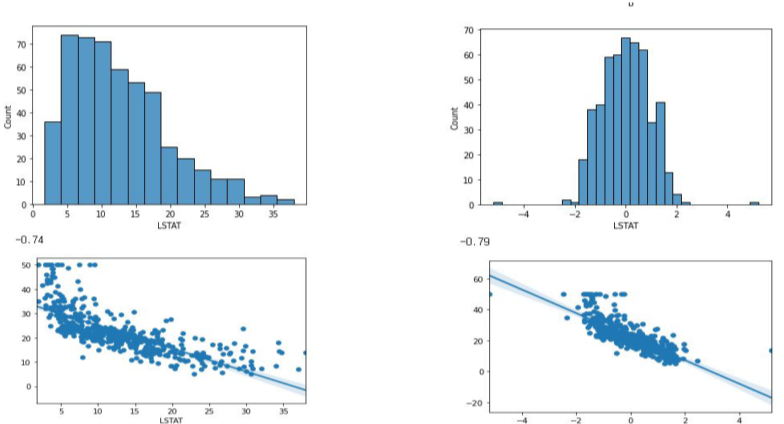
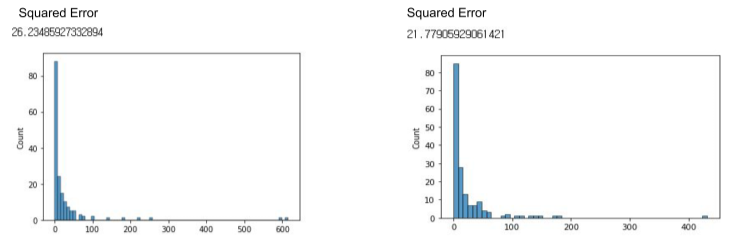
이러한 분포 변화를 통해 상관관계를 변경할 수 있다.

Binning

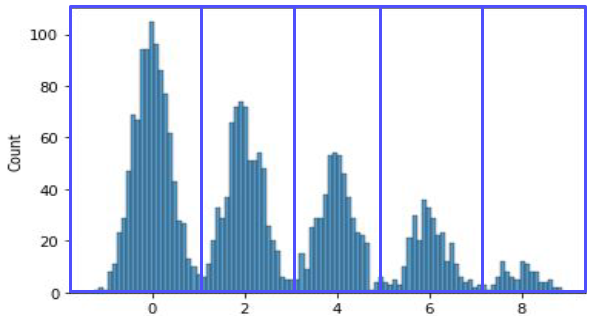
연속형 변수를 범주형 변수로 바꾸는 방법,

위와 같은 분포를 다봉분포라고 하는데 봉우리 마다 범주를 매길 수 있다.

Overfitting 방지에 탁월함, 선형 모델의 해석이 용이함

범주형 데이터 처리

출처:

categorical 데이터, 연속형 데이터보다 더욱 주의해야함.

보통 문자열로 이루어져 있지만, 이를 학습에 사용하기 위해 수치형 변수로 바꾸곤 함.

1. One hot encoding

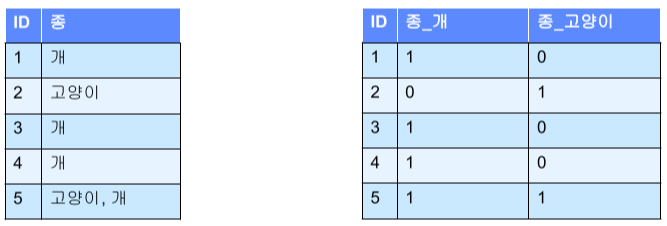
변수를 1과 0으로 나눈 후, 해당 값이 존재하면 1 아니면 0으로 놓는 방법

모델이 변수의 의미를 정확하게 파악할 수 있다는 장점이 있다.

단, 변수 갯수가 엄청나게 많아지면 sparse하고 크기가 커지게 된다.

차원의 저주 문제, 메모리 문제 야기함

1. Label encoding

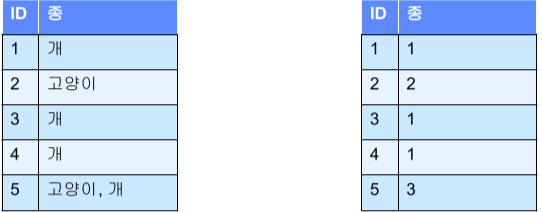
컬럼의 수는 1개로 유지하되, 각각의 값이 다른 의미를 가진 값을 부여해줌

위의 One hot encoding의 단점을 보완.

단, 모델이 이 숫자의 크기, 순서를 중요하게 생각하고 학습할 수 있음

특히 선형 모델에서는 순서와 상관없는 변수의 경우, Label encoding은 사용하면 안됨

1. Frequency encoding

   

해당 변수의 출현빈도를 변수의 값으로 사용하는 방법

1. Target encoding

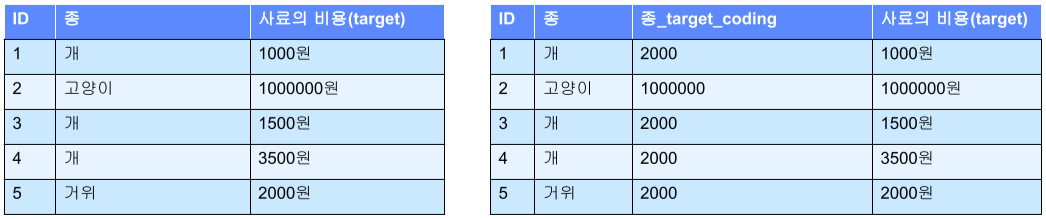
각각의 변수의 target 변수의 평균으로 encoding 하는 방식

Frequency encoding와 Target encoding은 순서와 크기가 중요한 경우이므로 encoding 값이 의미가 있어 학습이 되어도 상관 없다는 장점.

하지만, 다른 변수가 같은 값을 가질 수 있다는 단점, 미래에 새로 등장한 값의 경우 encoding할 수 없다는 단점, Target encoding의 경우 overfitting이 생길 수 있음

1. (Entity) Embedding

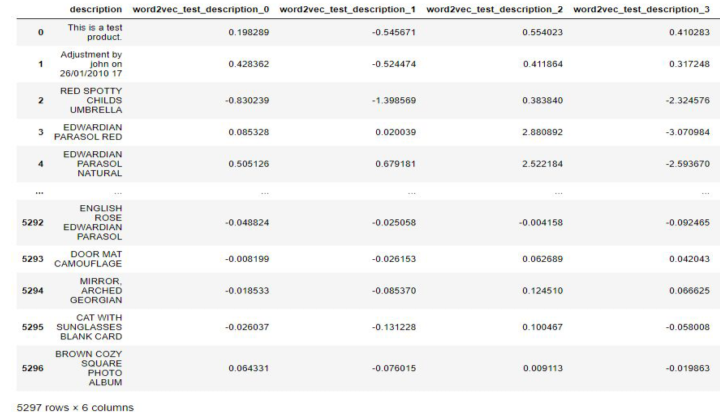
문자열같은 경우 내용이 길어 수치화 하기 힘들며, Word2Vec과 같은 알고리즘으로 수치화할 수 있다.

결측치 처리

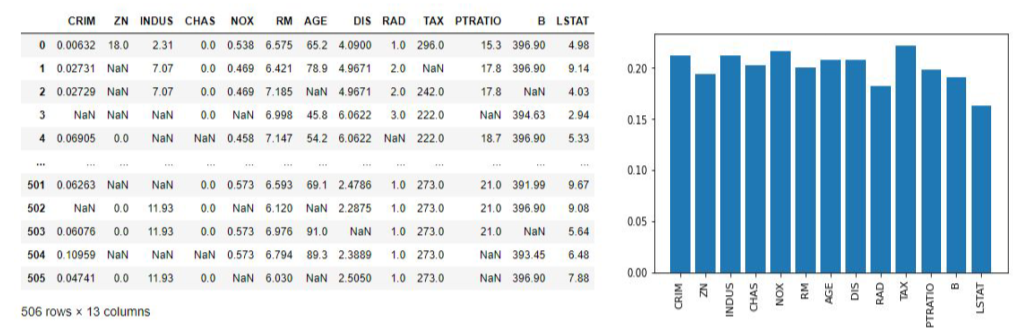
결측치는 위와 같이 NaN, 즉 측정하지 못하거나 손실 등의 여러 이유로 값이 존재하지 않는 경우를 의미한다.

pattern(결측치의 패턴 파악)

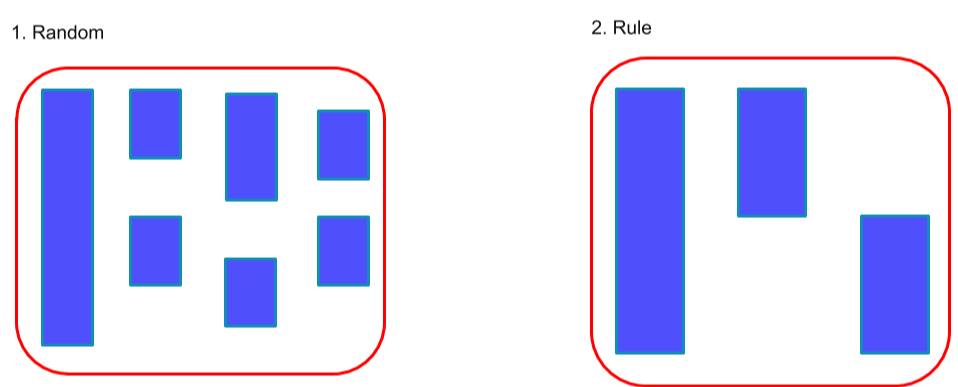
위와 같이 (흰색의 비어있는 부분이 결측치) 결측치의 생성은 랜덤한 경우와 일정한 패턴이 있는 경우로 나눠진다.

보통은 위와 같이 결측치의 패턴이 존재하지 않는 경우가 대부분이며 이때는 단변량이나 다변량 결측치 삽입을 사용해야한다.

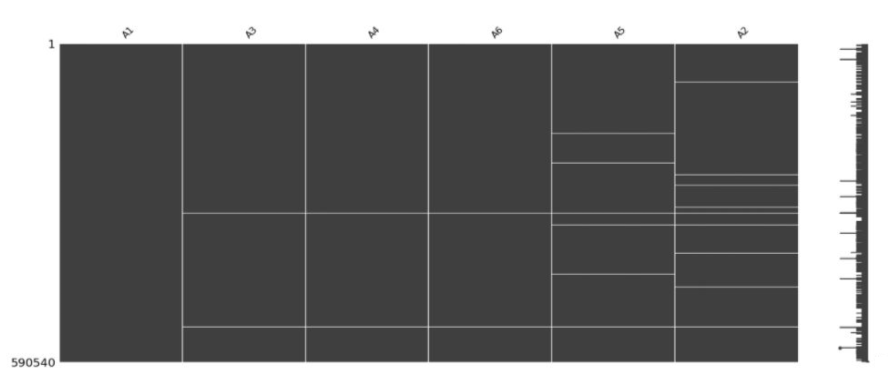
위와 같이 패턴이 존재하는 경우 패턴을 찾아낸 뒤, 결측치를 채울 방법을 고려해야 한다.

• A3에서 결측치가 존재한 경우 A4, A5,A6 모두 결측치가 존재함
• A1은 결측치가 없음 등

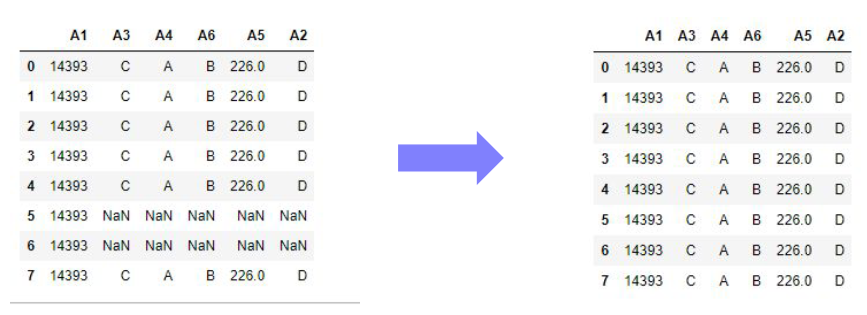
결측치가 존재하는 데이터의 나머지 변수와 비교해서 채워넣을 수 있다.

Univariate(단변량 결측치 삽입)

하나의 변수가 가진 결측치를 해당 변수를 통해서 채우는 방법

1) 데이터 포인트 제거

결측치가 있는 Row를 제거하거나, 변수 자체(Column)을 제거하는 방법

모델의 사용 데이터가 줄어드므로, 데이터가 적으면 좋지 않은 방법, 예측해야할 값(y)가 결측치일 경우, 삭제가 불가능한 경우도 있음.

2) 평균값 삽입

변수의 평균 값을 삽입하는 방법

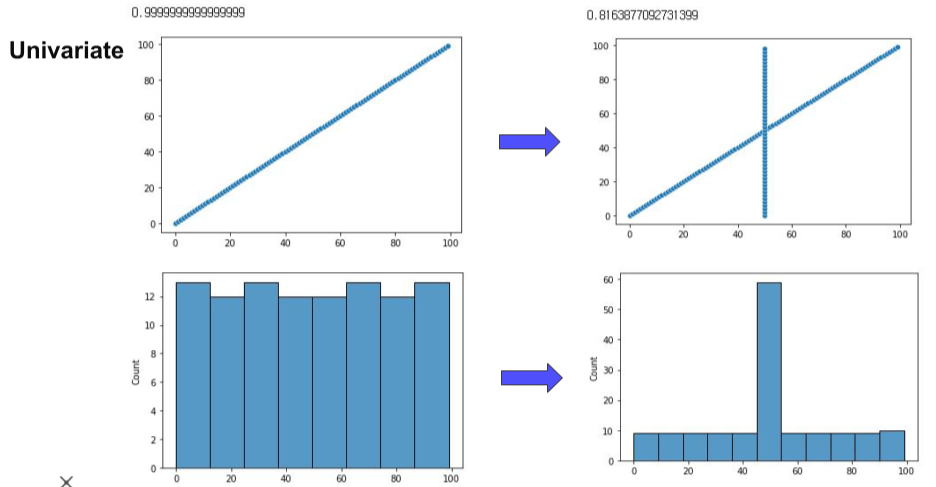
원래 좌측 상단의 그래프처럼 1:1의 정비례 관계의 그래프에서 중간 50 부분에 결측치가 생겨서, 이를 평균값인 50을 넣어주게 되면 비례관계와 분포가 바뀌게 된다.

3) 중위값 삽입

4) 상수값 삽입

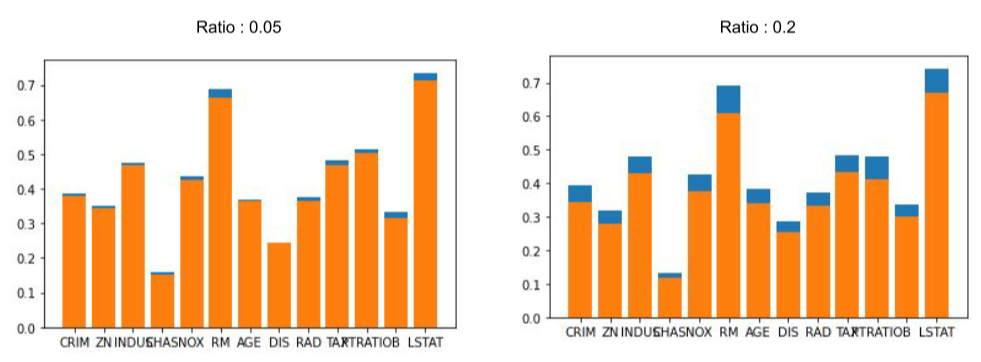
Univariate 방법은 모두 결측치가 너무 많으면 문제가 생길 수 있다.

Multivariate(다변량 결측치 삽입)

결측치 값을 머신러닝을 통해서 구하거나, 나머지 변수값을 비교하여 가장 비슷한 결측치 없는 Row의 값을 넣어주는 방법이 있다.

1. 회귀분석 : x1을 x2….Xn으로 예측, x2로 x1….xn 예측의 반복

2. KNN nearest : 결측치가 존재하는 샘플과 가장 유사한 샘플을 구함
3. 합리적 접근법

단, 결측치가 많아서 시행이 불가능하거나, 데이터가 너무 많아 시간이 너무 오래걸리는 경우도 있다.

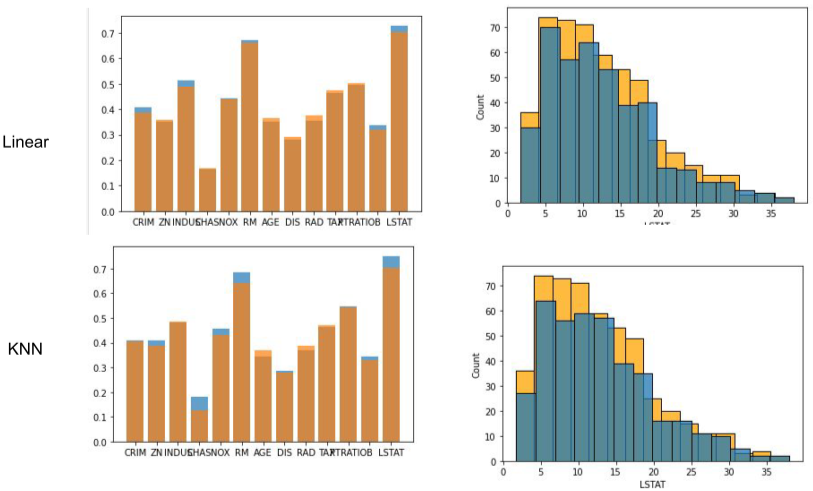
좌측 파란색이 결측치 채우기 전, 주황색이 결측치 채운 후의 상관관계이다.

우측 변수의 빈도 변화

단변량 보다는 훨씬 나은 결과를 보임을 알 수 있다.

합리적 접근법

다른 곳에서 데이터를 구하거나, 다른 변수를 통해서 구할 수 있다.

이상치 처리

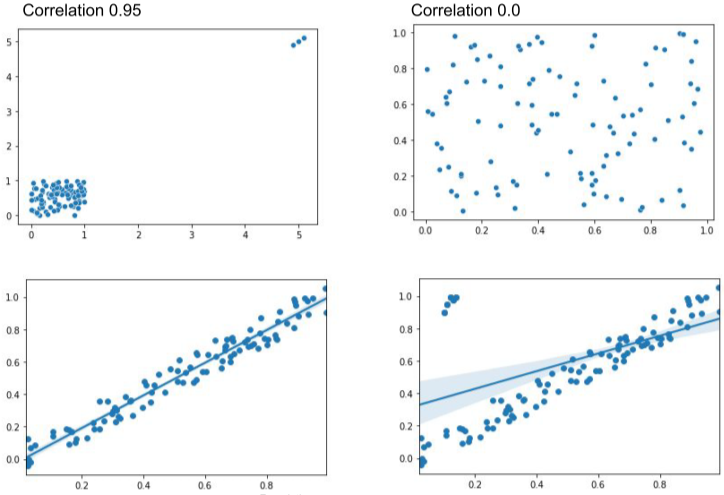
일반적인 데이터와 크게 다른 경우를 의미한다.

위의 경우 상단의 두 그래프는 좌(이상치가 있는 경우), 우 (이상치 제거한 경우)이며, 좌측은 x,y가 상관이 있어보이지만, 우측을 보면 x,y와 관계없이 랜덤하게 흩뿌려져있다.

아래의 그래프의 경우도 이상치 몇개로 인하여 선형모델이 학습한 기울기가 바뀌어 버린다.

이상치를 잘못 처리하면 커다란 영향이 간다.

tree 모델은 이상치에 덜 영향을 받긴한다.

이상치 탐색 방법 예시 두가지로, Z Score, IQR이 존재한다.

이상치 탐색 후, 이상치를 보는 관점에 따라 처리방법이 달라진다.

1. 정성적인 측면 : 이상치의 발생 이유는? 이상치의 의미는? 이를 통해 처리 방법을 고민

ex) 아파트 거래가 vs 아파트 건축연도에 대한 그래프에서, 보통 신축일 수록 비싼데, 60년된 은마아파트가 비싼 이유는 무엇인가? => 아파트의 위치, 재개발 여부 등에 따라 가격이 바뀔 수 있으므로, 위치, 재개발 여부 변수를 추가하여 이상치를 이상치가 아니게 만드는 방식으로 제거 가능

1. 성능적인 측면 : Train Test Distribution, 만약 Train과 Test 둘다 이상치가 존재하는데, Trian set에서만 이상치를 없애버리면, 예측력이 떨어지게 됨.

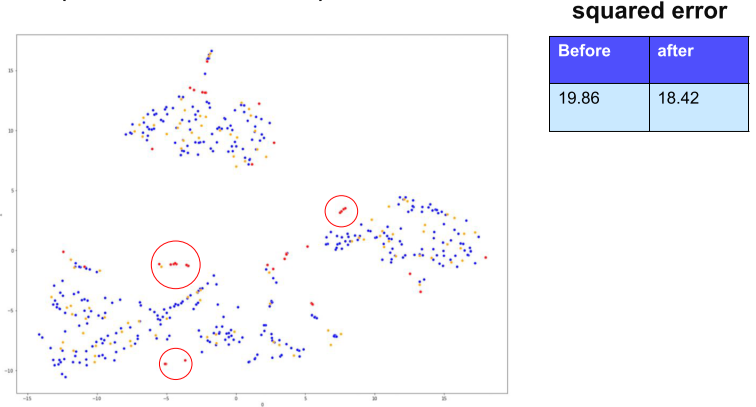
파랑색 점이 Train, 노랑색 점이 Test, 빨간색 점이 Z Score로 구한 이상치일 때,

이상치 점들이 Test 점들과 겹치지 않는 경우가 많으므로, 제거하면 모델 성능이 올라간다.

머신 러닝 개념

Underfitting & Overfitting

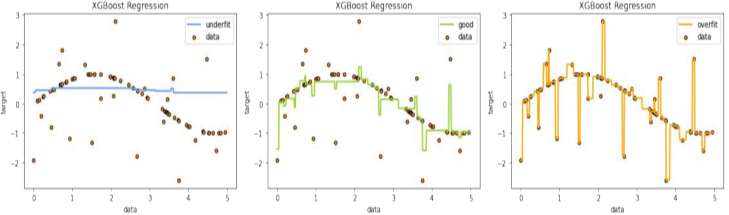
Underfitting은 너무 데이터셋에 맞지 않는 예측곡선을 그린 경우,

Overfitting은 너무 데이터셋에 맞는 예측곡선을 그린 경우이다.

이론상 우리가 모든 데이터를 이용해 데이터셋을 만들거나 분포가 완전 동일하다면, Overfitting된 그래프가 최적이지만, 실제로는 일부분만 사용하므로 적절하지 않다.

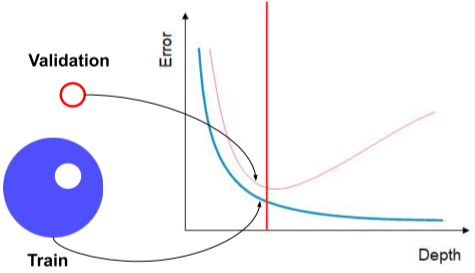
Overfitting 여부를 확인하기 위해 Validation dataset을 따로 두어, Train Accuracy와 Validation Accuracy를 비교하여 격차가 벌어지기 시작하는 점 이후로 는 Overfitting 되가는 것이다.

Underfitting 현상을 방지하기 위해서는

1) 더 많은 데이터로 더 오래 학습

2) feature를 더욱 많이 반영

3) Variance가 높은 모델 활용

Overfitting 현상을 방지하기 위해서는 Regularization(정규화) 방법이 있으며

모델이 Noise에도 크게 반응하지 않게 규제하는 방법이다.

Regularization에는 다음으로 나뉜다.

1) 정형 데이터에서 사용 불가능한 방법

• Noise robustness
• Label smoothing
• Batch normalization

2) 정형데이터에서 사용 가능한 방법

• Early stopping

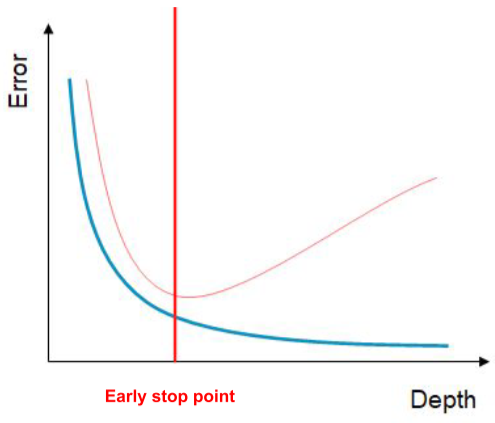
Training data와 비교하여 Validation 성능이 떨어지려할 때 멈추는 방법

• Parameter norm penalty

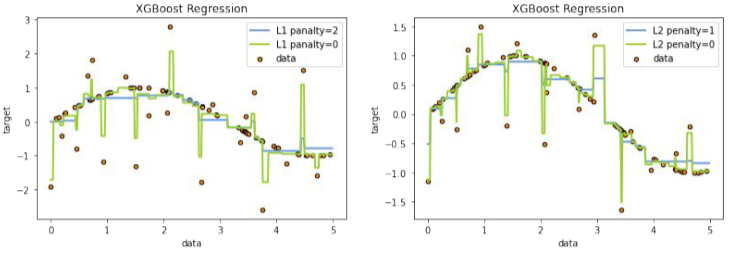
noise에 민감하지 않게 모델을 만들 수 있음

L1 : Lasso 페널티

L2 : Ridge? 페널티

페널티 계수를 조절해서 overfitting을 줄일 수 있다.

하이퍼파라미터로도 사용할 수 있다.

• Data augmentation

원본 데이터를 변형하여 데이터를 증강시켜 사용하는 방법

SMOTE : 정형데이터에서의 데이터 증강방법

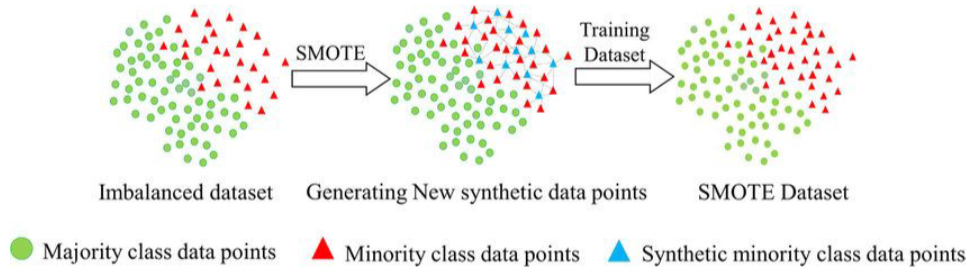
주로 Imbalance한 데이터들을 대상으로 근처의 데이터를 생성하여 데이터 증강

• Dropout

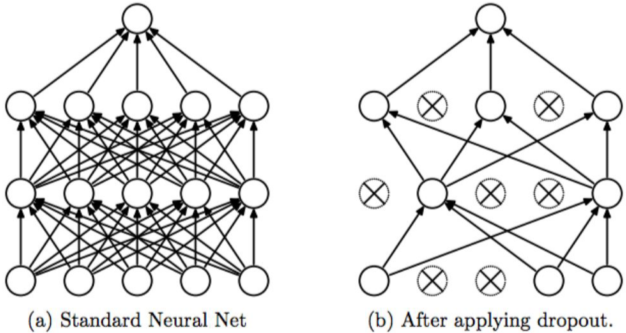
가지치기, 무작위로 노드의 연결을 끊어버려 일부 feature만 사용하여 모델을 생성

정형 데이터에서는 Tree model 등에서 사용할 수 있으며, 모두 사용하는 것이 아닌 랜덤 샘플링 등이 예시이다.

Validation strategy

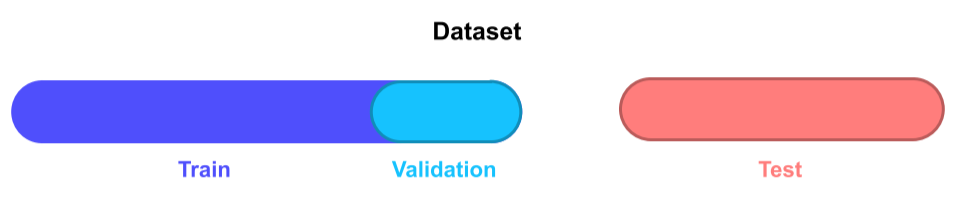
Validation strategy는 데이터셋을 각 Train, Validation, Test 세가지로 나누어 학습시키는 방법이다.

먼저 Test 데이터셋은 프로젝트 결과와 직결되는 데이터셋이므로 설정을 신경써서 해야한다.

• 최대한 전체 데이터셋을 대표할 수 있는 데이터셋이어야 함,
  • 데이터를 바꿀 때 마다 성능이 달라짐
  • 즉, 왠만하면 안바꿔야 함

Validation dataset은 내가 만든 모델을 Test 데이터셋에 적용하기 전에 모델의 성능을 파악하기 위한 데이터셋이며, 이때 파악한 성능으로 Early stop이나 기타 Regularization 기법을 활용 가능

• 테스트 데이터셋과 최대한 비슷하게, 즉 전체 데이터셋을 대표할 수 있게 구성해야함.
  • 테스트 데이터셋을 알 수 없는 경우(미래에 있거나, competition이라 가려져 있거나), 전체 데이터셋을 대표할 수 있게 구성해야 한다.
  • 예를 들어, 모래먼지가 자주 부는 지방에서 object detection => Validation set에서 모래먼지가 낀 듯한 데이터의 비율이 좀더 많아야함.

Train dataset은 모델이 보고 학습하는 데이터로, 보통 Validation dataset과 Test dataset을 정한 뒤 남은 것을 사용하나, 이때, noise 데이터를 포함하냐 안하냐가 중요하다.

Hold-out validation

Hold-out validation은 하나의 고정된 Validation set을 지정하는 방식이다.

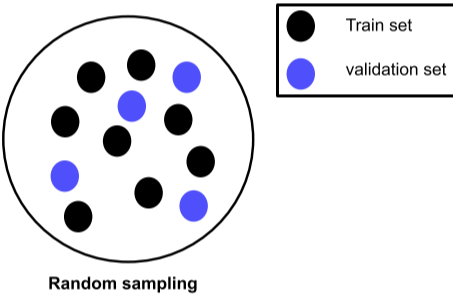
Random sampling

랜덤으로 Validation을 정하는 방법으로 class가 imbalance하게 될 수 있으므로 잘 사용하지 않는다.

단, 데이터셋이 아주 방대하면 Test dataset과 비슷하게 나오기도 한다.

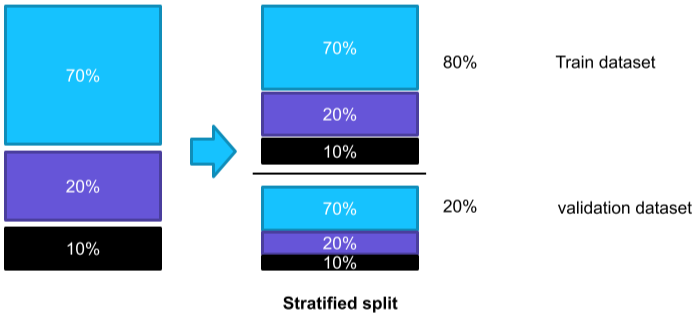
Stratified split

각각의 label의 비율을 train과 validation set이 비슷하게 만드는 방식이다.

보통 Train과 Validation은 8:2 비율이며, 데이터가 많으면 9:1, Test를 많이 하면 7:3까지 늘리기도 한다.

Cross Validation

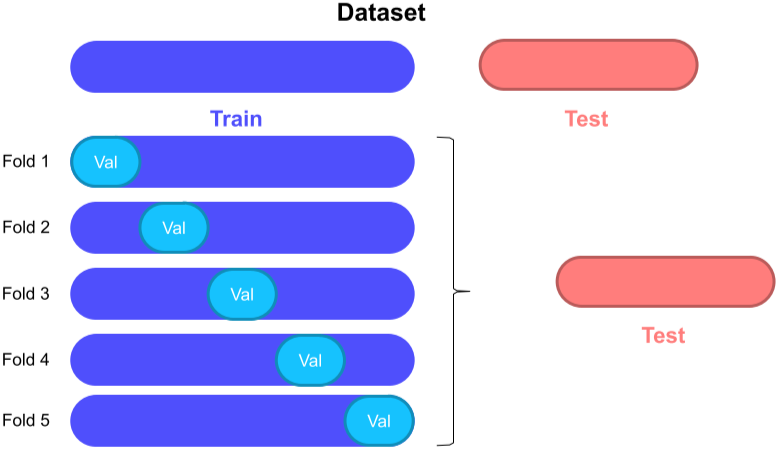
Train과 Validation set을 여러 부분에서 가져와 학습시킨 모델들을 앙상블을 통해 계산하는 방법, 특히 K-fold cross validation이라고 함.

위의 두 샘플링 방법, 랜덤과 Stratified 둘다 사용할 수 있다.

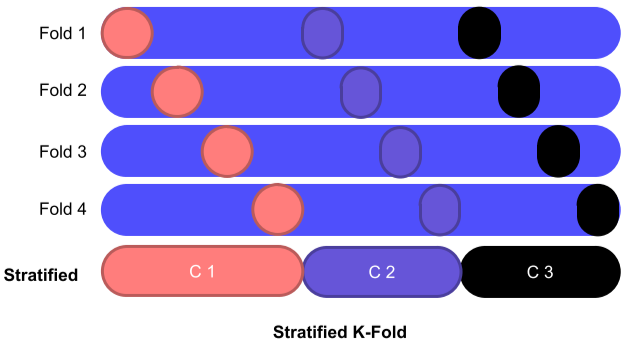
Lable의 비율을 맞추고 k개로 나누는 방법, 많이 사용함.

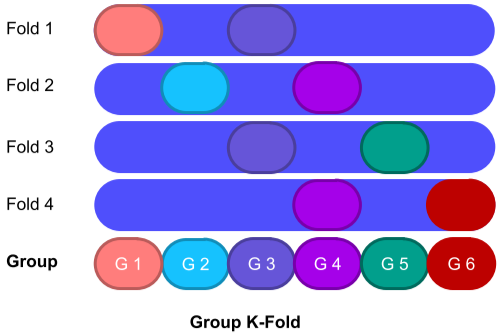
Group(label이 혼재되어 있음)들을 하나의 덩어리로 생각하고 같은 fold에는 들어가지 않도록 Split 함, Group의 수는 언제나 fold의 수 k보다 커야한다.

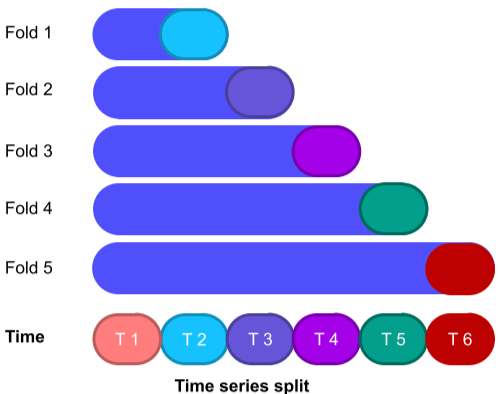
시계열 데이터셋의 경우 시간을 기준으로 validation set을 나누어, 미래 데이터가 과거 데이터에 영향을 받지 않도록 하는 방법이 있음

앞쪽 fold 일수록 data가 적어짐

Reproducibility(재연성)

모델의 학습 성능을 다시 학습하여 재연하기 위해서 랜덤성을 제거해줘야한다.

이를 위해 랜덤 seed를 고정해줘야 한다.

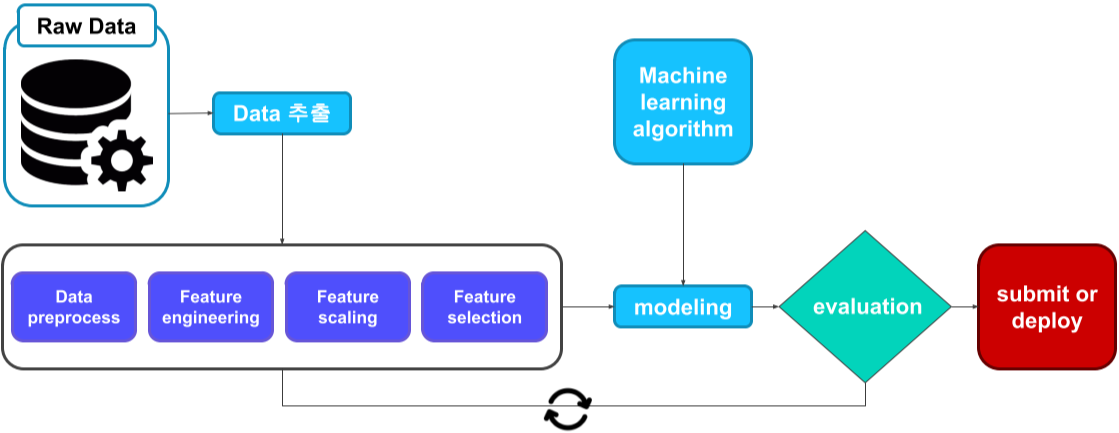
Machine learning workflow

트리 모델 소개

What is tree model

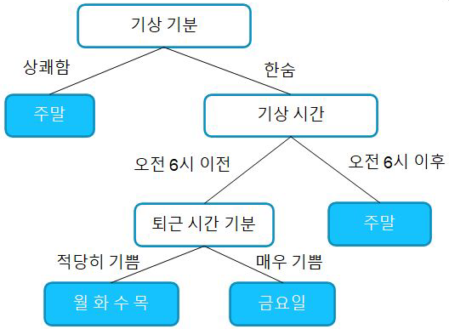
트리 모델이란, 칼럼(feature) 값들을 어떠한 기준으로 Group을 나누어 목적에 맞는 의사결정을 만드는 방법

질문으로 yes or no로 descision을 내리는 의사결정나무를 생성하여 만든다.

Decision Tree, Random Forest, AdaBoost, GBM, XGBoost, LightGBM, CatBoost 순으로 발전해 왔다.

Bagging & Boosting

트리 모델을 만들때 사용한 방법

Decision Tree 여러개를 이용하여 모델을 생성하며, Training data의 활용법에 따라 Bagging과 Boosting으로 나뉜다.

1. Bagging

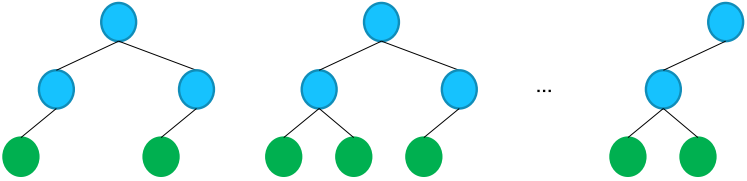
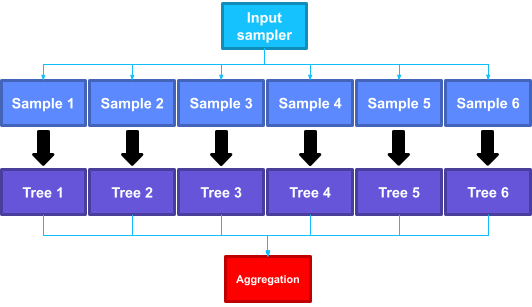
• 랜덤 포레스트의 생성 방법

• 데이터셋을 샘플링하여 모델을 만들어 나가는 방법
  • Bootstrap + Aggregation으로 이루어진다
  • Bootstrap: Data를 여러번 sampling, Aggregation : 종합(ensemble)
• 샘플링한 데이터 셋을 하나로 하나의 Decision Tree 생성
• 생성한 Decision Tree의 Decision들을 취합(aggregation)하여 하나의 Deicision 생성

1. Boosting

Tree model with hyper-parameter