AI 수학 기본

Dec 14, 2022

1. Vector
   • 벡터란?
   • 벡터의 성질
   • 벡터 노름(norm)과 기하학적 성질
2. Matrix
   • 행렬이란?
   • 행렬의 이해
   • 행렬의 곱셈(matrix multiplication)과 내적
   • 역행렬의 이해
   • 행렬의 응용
3. Gradient Algorithm(경사하강법)
   • 미분 (differentiation)이란?
   • 미분 활용
   • 경사하강법 (Gradient Algorithm) 구현
   • 그레디언트 벡터 (Gradient vector) 이용한 경사하강법
   • 경사하강법의 선형 회귀 적용 (apply to linear regression)
   • 확률적 경사하강법 (stochastic gradient descent)
4. 인공지능 학습의 수학적 이해
   • 신경망의 해석
   • 소프트맥스 연산
   • 활성화 함수(activation function)와 다층 신경망(MLP)
   • 역전파(backpropagation) 알고리즘
5. 확률론
   • 확률분포
   • 기대값
   • 몬테카를로 샘플링(Monte Carlo sampling)
6. 통계학
   • 모수
   • 데이터 모수 추정
   • 최대 가능도(maximum likelihood estimation, MLE) 추정
7. 베이즈 통계학
   • 조건부 확률
   • 베이즈 정리를 통한 정보의 갱신
   • 조건부확률과 인과관계의 차이
8. CNN
   • CNN(Convolution Neural Network)의 이해
   • 다차원 CNN(Convolution Neural Network)의 이해
   • CNN의 역전파
9. RNN
   • 시퀀스(sequence) 데이터
   • RNN의 이해와 BPTT

AIMath

Vector

벡터란?

• 숫자를 원소로 가지는 리스트 또는 배열을 의미

  벡터의 코딩상 의미

  

• $X$ = 열 벡터, $X^T$ = 행 벡터

• 수학적으로는 공간에서의 한 점, 원점으로 부터의 상대적 위치를 의미

  벡터의 수학적 의미

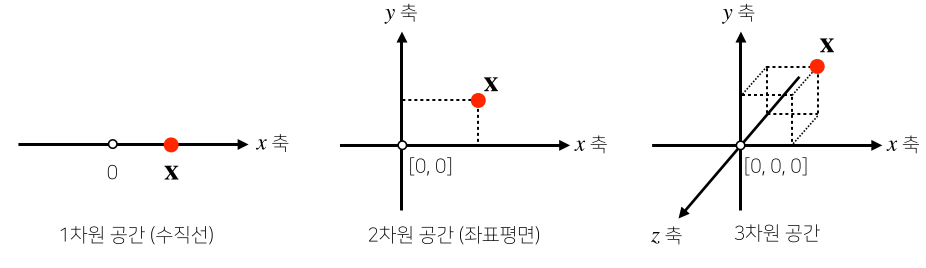
• 각 벡터가 가지는 행과 열의 수를 벡터의 차원이라고 한다.

벡터의 성질

1. 벡터에 양수를 곱해주면 방향은 그대로, 길이만 변한다.

• 이 때 곱해주는 숫자를 스칼라곱($\alpha$)이라고 표현한다.

• 스칼라곱이 음수이면 방향이 정반대 방향이 된다.

• 벡터의 길이는 1보다 크면 길이가 증가, 1보다 작으면 길이가 감소한다.
  2. 같은 모양(같은 행과 열)을 가지면 덧셈, 뺄셈, 곱셈, 나눗셈이 가능하다.
  - 이때의 곱셈을 성분곱(Hadamard product)라고 한다.
  - numpy array에도 적용된다.
  3. 벡터와 벡터의 덧셈과 뺄셈은 다른 벡터로부터 상대적 위치 이동을 표현함.

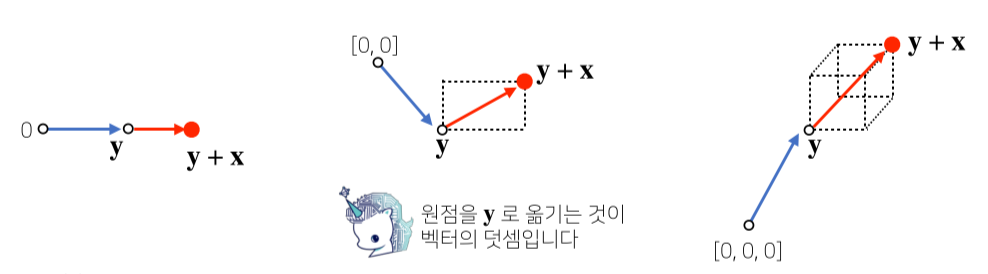
벡터 노름(norm)과 기하학적 성질

벡터의 노름

• 벡터의 노름(norm)은 원점에서부터의 거리를 의미

  • 차원의 수와 관계없이 모든 벡터는 노름을 구할 수 있다.
  • L~1~-노름은 각 성분의 변화량의 절대값의 합을 의미
    • $(x,y)$는 $|x|+|y|$ 만큼 거리
  • L~2~-노름은 피타고라스 정리를 이용해 유클리드 거리를 계산
    • $(x,y)$는 $\sqrt{|x|^2 +|y|^2}$를 의미
    • np.linalg.norm으로 구현 가능
  • $\parallel \parallel $ 기호는 노름이라고 부름
  \[\parallel x\parallel_1 = \sum_{i=1}^d|x_i|\\ \parallel x\parallel_2 = \sqrt{\sum_{i=1}^d|x_i|^2}\\\]

백터 노름의 코드 구현

def l1_norm(x):
    x_norm = np.abs(x)
    x_norm = np.sum(x_norm)
    return x_norm

def l2_norm(x):
    x_norm = x*x
    x_norm = np.sum(x_norm)
    x_norm = np.sqrt(x_norm)
    return x_norm

노름의 활용과 성질

• 노름의 종류를 무엇으로 적용하느냐에 따라 기하학적 성질이 달라진다.

  • L1 노름은 마름모 모양의 원을 그리며, L2 노름은 기존의 원 모양의 원을 가진다.
  • 노름의 종류에 따라 머신러닝에서의 활용도 달라진다.

• 노름을 이용해 두 벡터 사이의 거리를 뺄셈을 통하여 계산할 수 있다.

  

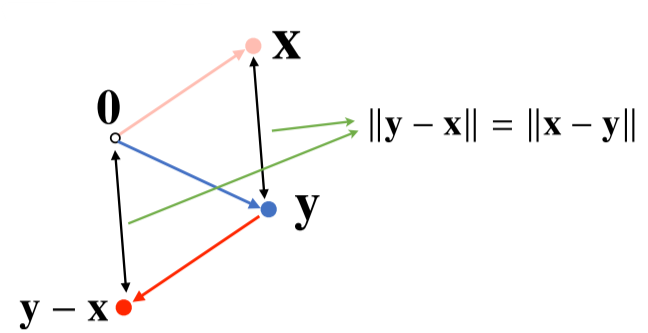
  • $\parallel y - x\parallel = \parallel x - y\parallel$ 인점을 이용하게 된다.
  • 즉 x-y 또는 y-x를 한 원점에서의 좌표를 이용해 L2 norm을 구하면 두벡터 사이의 거리가 나온다.

• L2 노름 한정으로 내적을 이용해 이렇게 구한 벡터사이의 거리를 이용해 각도 또한 계산 가능하다.

  

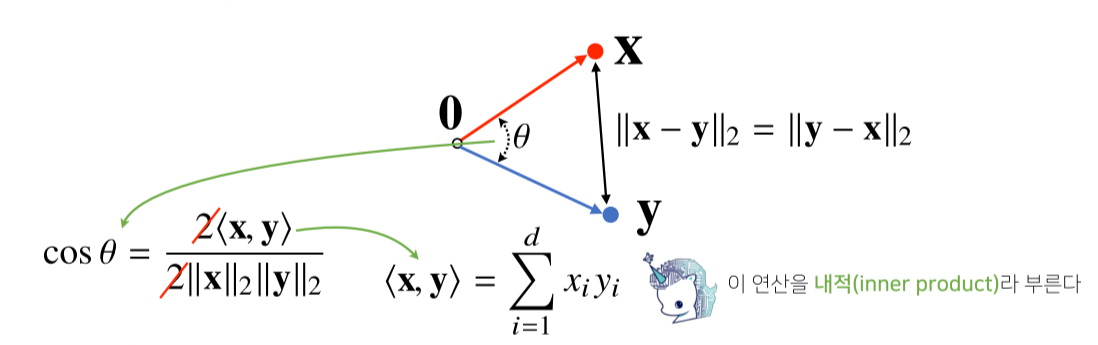
  • <x, y> 는 내적(inner product)을 의미하며 성분 곱들의 합을 의미한다.
    • 예를 들어 x = (0, 1), y = (0, 2)의 내적은 0 * 0 + 1 * 2 = 2 이다.

내적을 이용한 각도 계산

def angle(x,y):
    # np.inner(x, y)가 내적을 구하는 numpy 함수
    v = np.inner(x, y) / (l2_norm(x) * l2_norm(y))
    theta = np.arccos(v)
    return theta

내적의 해석

• 내적은 정사영(orthogonal projection)된 벡터의 길이와 관련 있다.

  • Proj(x)는 벡터 y로 정사영된 벡터 x의 그림자를 의미한다.
  • Proj(x)의 길이는 코사인법칙에 의해

\[\parallel x \parallel cos\theta\]

• 가 된다.

  

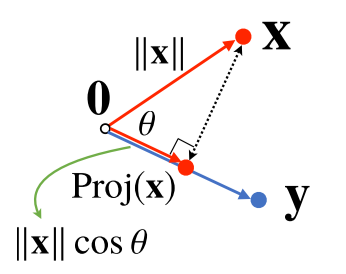
• 이때 내적은 정사영의 길이를 벡터 y의 길이 $\parallel y \parallel$만큼 조정한(곱한) 값이다.

• 내적을 이용해 유사도(similarity)를 구할 수 있다.

Matrix

행렬이란?

• 벡터를 원소로 가지는 2차원 배열

행렬의 수식 표현

\[X = \begin{bmatrix} 1 & -2 & 3 \\ 7 & 5 & 0 \\ -2 & -1 & 2\end{bmatrix}\]

행렬의 코드 표현

x = np.array([[1, -2, 3], [7, 5, 0], [-2, -1, 2]]) # numpy에선 행(row)이 기본단위

\(\boldsymbol{X} = \begin{bmatrix}symbol{x_{1}} \\symbol{x_{2}} \\symbol{\vdots}\\symbol{x_{n}} \end{bmatrix} = \begin{bmatrix} x_{11} & x_{12} & \dots & x_{1m}\\ x_{21} & x_{22} & \dots & y_{2m}\\ \vdots & \vdots & & \vdots\\ x_{n1} & x_{n2} & \dots & x_{nm}\end{bmatrix} \begin{aligned}\boldsymbol{x_{1}}\\symbol{x_{2}}\\symbol{x_{7}}\end{aligned}\)

• n x m 행렬의 표현

• 행렬은 행(row)과 열(column)이라는 인덱스(index)를 가집니다.

• 행렬의 특정 행이나 열을 고정하면 행 벡터 또는 열 벡터라 부른다.

• 전치 행렬(transpose matrix) $X^T$는 행과 열의 인덱스가 바뀐 행렬을 의미함.

• 벡터 또한 동일하게 행과 열이 바뀐 전치 벡터가 존재한다.

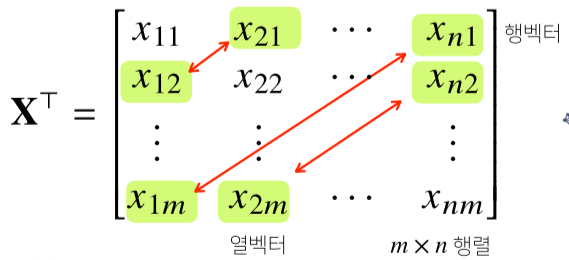
행렬의 이해

1. 첫번째 의미

• 벡터가 공간의 한점을 의미한다면 행렬은 공간에서 여러 점들의 집합을 의미함.
• 행렬의 행벡터 $x_i$는 i번째 데이터를 의미함.
• 행렬 $x_{ij}$는 i번째 데이터의 j 번째 변수값을 의미함.

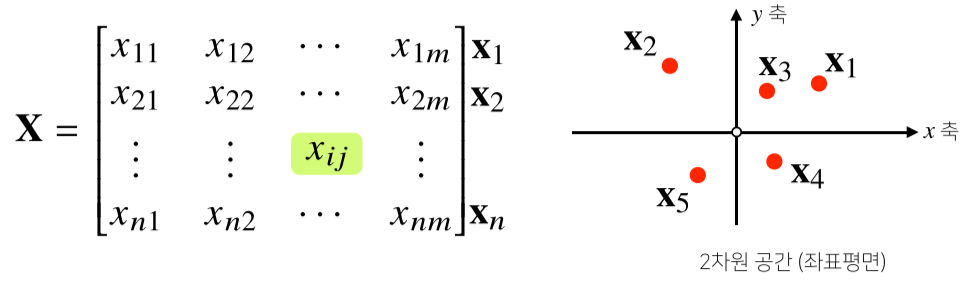
• 벡터와 마찬가지로 같은 모양을 가지면 같은 인덱스 위치끼리 덧셈, 뺄셈. 성분곱을 계산할 수 있다.
• 벡터와 마찬가지로 스칼라곱($\alpha$) 또한 가능하다.

2. 두번째 의미

• 행렬은 벡터 공간에서 사용되는 연산자(operator)를 의미.
• 행렬 곱을 통해 벡터를 다른 차원의 공간을 보낼 수 있음
  • 행렬을 X벡터와 곱하면 m차원에서 n차원 벡터로 변환되어 n차원의 z벡터가 됨.
  • 이를 통해 맵핑, 디코딩 등이 가능함.
  • 이를 선형 변환(linear transform)이라고도 함.
  • 딥러닝은 선형 변환과 비선형 변환의 합성으로 이루어짐
• 패턴 추출, 데이터 압축 등에도 사용함.

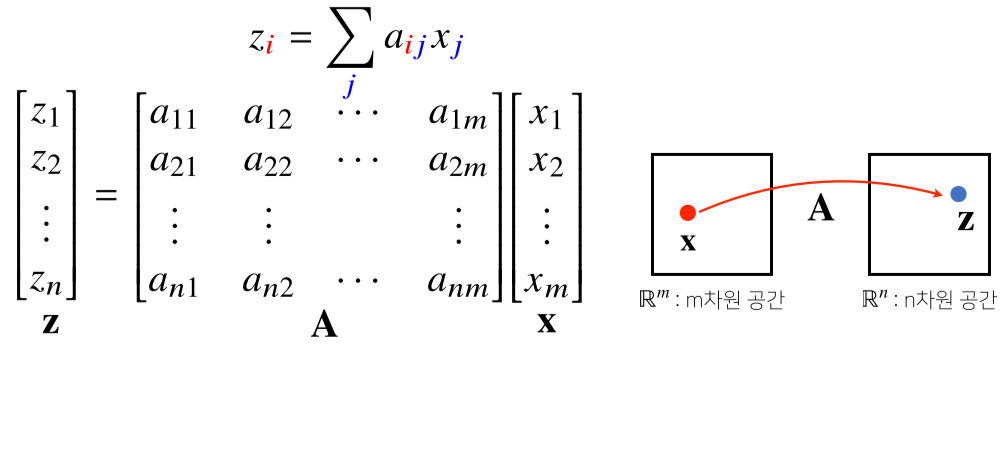
행렬의 곱셈(matrix multiplication)과 내적

1. 행렬의 곱셈(matrix multiplication)

• 행렬 곱셈은 i번째 행벡터와 j 번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 만듭니다.

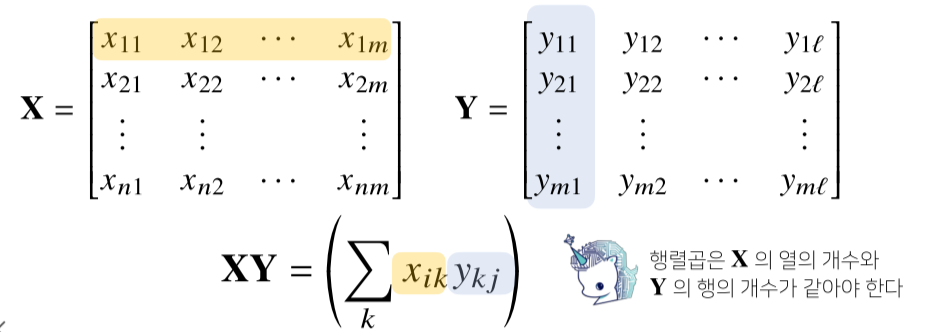
• 고로 행과 열의 갯수가 같아야 가능하다.

행렬의 곱셈 code 구현 시

X = np.array([[1, -2, 3],
            	[7, 5, 0],
            	[-2, -1, 3]])
Y = np.array([[0, 1],
            	[1, -1],
            	[-2, 1]])
print(x @ Y) # numpy에선 @ 연산으로 행렬 곱셈 계산
# array([[-8, 6],
#        	[5, 2],
#         	[-5, 1]])

2. 행렬의 내적

• np.inner는 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산합니다.
• 수학의 행렬 내적 $tr(XY^T)$과 다름

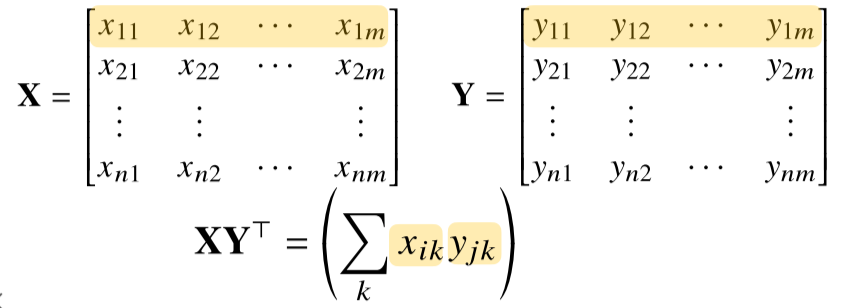
행렬의 내적 code 구현 시

X = np.array([[1, -2, 3],
            	[7, 5, 0],
            	[-2, -1, 3]])
Y = np.array([[0, 1, -1],
            	[1, -1, 0]])
print(np.inner(x, Y)) # numpy에선 np.inner() 함수로 행렬 내적 계산
# array([[-5, 3],
#        	[5, 2],
#         	[-3, -1]])

역행렬의 이해

• 행렬 A의 연산을 같은 연산으로 거꾸로 돌리는 행렬을 역행렬(Inverse matrix)라고 부르며, $A^{-1}$라 표기한다.
• 행과 열 숫자가 같고 행렬식(determinant)가 0이 아닌 경우에만 계산 가능.

역행렬과의 행렬곱의 결과

\[AA^{-1} = A^{-1}A = I(항등행렬)\]

• 항등행렬(Identity Matrix)은 곱하게 될 시 자기 자신이 나오는 행렬이다.

역행렬의 코드 구현

Y = np.array([[1, -2, 3], [7, 5, 0], [-2,-1,2]])
print(Y @ np.linalg.inv(Y)) # np.linalg.inv(Y) Y 행렬의 역행렬이 리턴
# array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) # 정확히는 float으로 비슷한 값이 나온다.

• 역행렬을 계산할 수 없는 조건이라면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 $A^ +$을 이용한다.

유사역행렬의 성질

\[n \geq m 인\ 경우, \ A^+ = (A^TA)^{-1}A^T,\ A^+A = I\\ n \leq m 인\ 경우, \ A^+ = A^T(A^TA)^{-1},\ AA^+ = I\\\]

• 순서를 바꾸면 결과가 달라지므로 유사역행렬의 순서에 주의!

유사 역행렬의 코드 구현

Y = np.aray([[0, 1], [1,-1], [-2,1]])
print(Y @ np.linalg.pinv(Y)) # np.linalg.pinv(Y) Y 행렬의 유사역행렬이 리턴
# array([[1, 0], [0, 1]]) # 정확히는 float으로 비슷한 값이 나온다.

행렬의 응용

1. 연립방정식 풀기

\[a_{11}x_1 + a_{12}x_2 + \dots + a_{1m}x_{m} = b_{1}\\ a_{12}x_1 + a_{22}x_2 + \dots + a_{2m}x_{m} = b_{2}\\ \vdots\\ a_{n1}x_1 + a_{n2}x_2 + \dots + a_{nm}x_{m} = b_{n}\\ n \leq m \ 인\ 경우:\ 식이\ 변수\ 개수보다\ 작거나\ 같아야\ 함\]

sol) n이 m보다 작거나 같으면 무어-펜로즈 역행렬을 이용해 해를 하나 구할 수 있다.
\(Ax = B \\ \Rightarrow x = A^+b\\ =A^T(AA^T)^{-1}b\)

2. 선형회귀분석

• np.linalg.pinv를 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있다.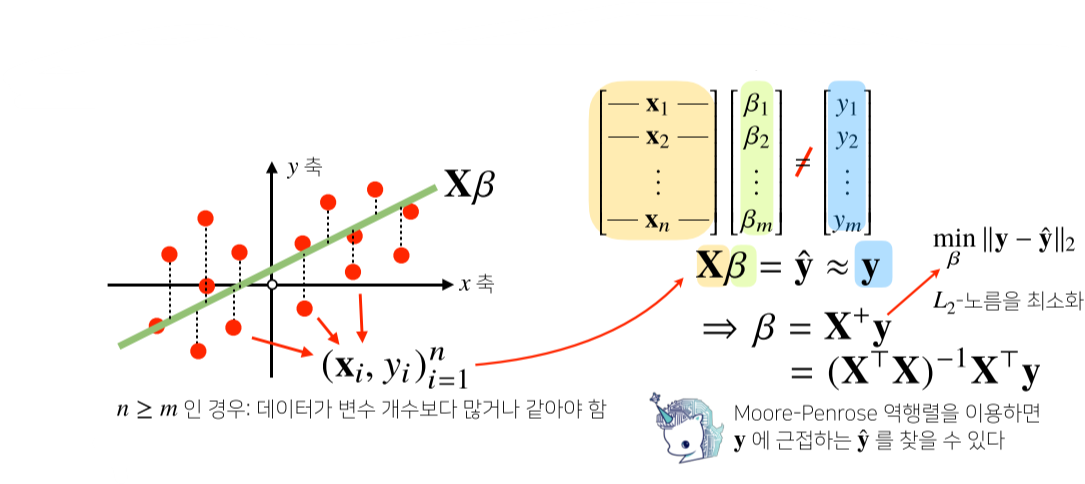

• sklearn의 LinearRegression과 같은 결과를 가져옴

# Scikit Learn을 활용한 회귀분석
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x,y)
y_test = model.predict(x_test)

# Moore-Penrose 역행렬, y절편(intercept)항을 직접 추가해야한다.
X_ = np.array([np.append(x,[1]) for x in X]) # intercept 항 추가
beta = np.linalog.pinv(X_) @ y
y_test = np.append(x, [1]) @ beta

Gradient Algorithm(경사하강법)

미분 (differentiation)이란?

• 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구.
• 변화율의 극한, 최적화에서 제일 많이 사용하는 기법.

\[f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h) - f(x)}h\]

미분 코드 구현

import sympy as sym # 기호를 통해 함수를 이해하게 해줌
from sympy.abc import x

sym.diff(sym.poly(x**2 + 2*x + 3), x)
#Poly(2*x + 2, x, domain='zz')

미분 활용

• 함수 그래프의 접선의 기울기와도 같으며, 이를 통해 함수값의 증감을 알 수 있다.

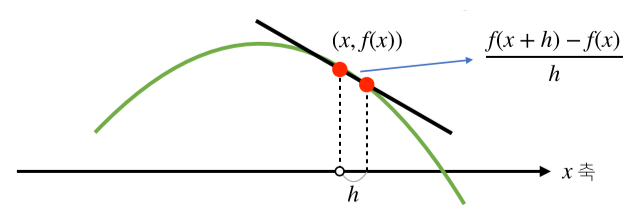
• 이렇게 구한 기울기를 통하여 미분값을 더하거나 빼서, 고차원 공간에서도 최적화 가능

  • 
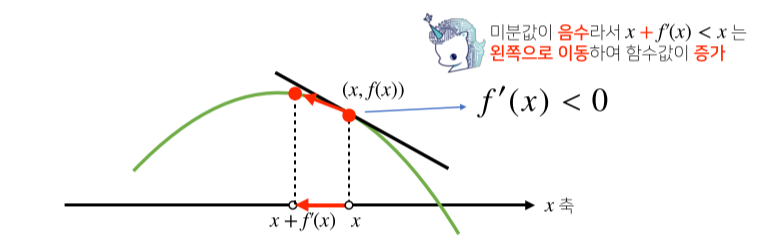
  • 미분값을 더하면 경사상승법이라 하며, 함수의 극대값을 찾는데 사용
  • 미분값을 빼면 경사하강법이라 하며, 함수의 극소값을 찾는데 사용

• 극소값이나 극대값에 도달하면 미분값이 0이므로 최적화가 종료됨.

  

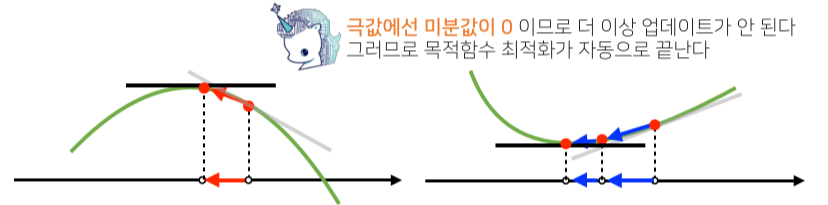
경사하강법 (Gradient Algorithm) 구현

코드 구현 슈도 코드

Input : gradeint, init, lr, eps, Output: var
# gradient: 미분을 계산하는 함수
# init: 시작점, lr: 학습률, eps: 알고리즘 종료 조건

var = init
grad = gradient(var)
while(abs(grad) > eps): # 미분값이 정확이 0이 되는 경우는 거의 없음, 즉 아주 작은값(eps)이하가 되면 종료
    var = var - lr * grad # lr: 학습률이 높을수록 넓게 업데이트함, 너무 크거나 작으면 안됨
    grad = gradient(var) # 미분값 업데이트

다변수 함수일 경우?

• 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용.

\[\partial _{x_{i}}f\left( x\right) =\lim _{h\rightarrow 0}\dfrac{f\left( x+he_{i}\right) -f\left( x\right) }{h}\\ e_{i}\ :\ i번째\ 값만 \ 1이고\ 나머지는\ 0인\ 단위벡터\]

코딩을 이용한 편미분

import sympy as sym
from sympy.abc import x, y

sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2*y), x)
# 2*x + 2*y - sin(x+2*y)

• 각 변수 별로 편미분을 계산한 그레이언트 벡터를 이용하여 경사하강/경사상승법에 사용 가능.

\[\partial _{x_{i}}f\left( x\right) =\lim _{h\rightarrow 0}\dfrac{f\left( x+he_{i}\right) -f\left( x\right) }{h}\\ e_{i}\ :\ i번째\ 값만 \ 1이고\ 나머지는\ 0인\ 단위벡터 \\ \nabla f = (\partial_{x1}f,\partial_{x2}f,\dots,\partial_{xd}f)\]

그레디언트 벡터 (Gradient vector) 이용한 경사하강법

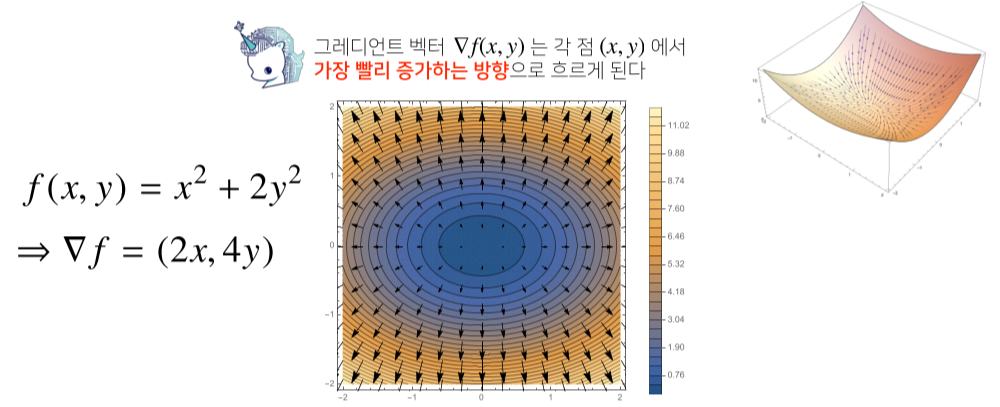
• ∇f (x,y)는 임의의 점(x,y)에서 가장 빨리 함수값이 증가하는 방향이다
• 그러므로 -∇f (x,y)방향으로 가면 가장 빨리 함수값이 감소하는 방향이 되며, 이를 적용해 경사하강을 한다.

그레디언트 벡터가 적용된 경사하강법 슈도코드

Input : gradeint, init, lr, eps, Output: var
# gradient: 그레디언트 벡터를 계산하는 함수
# init: 시작점, lr: 학습률, eps: 알고리즘 종료 조건

var = init
grad = gradient(var)
while(norm(grad) > eps): # 벡터의 절대값 대신 노름(norm)을 계산해 종료조건 설정
    var = var - lr * grad # lr: 학습률이 높을수록 넓게 업데이트함, 너무 크거나 작으면 안됨
    grad = gradient(var) # 미분값 업데이트

경사하강법의 선형 회귀 적용 (apply to linear regression)

• 무어-펜로즈 행렬을 이용해서 선형회귀가 가능했지만, 경사하강법을 이용하는게 일반적이다.

• **선형회귀의 목적식은 ∥y-Xβ∥~2~ 또는 ∥y-Xβ∥~2~^2^ ** 이며, 이를 최소하하는 β를 찾는게 목적이므로 다음과 같은 그레디언트 벡터를 구해야한다.(loss : RMSE 기준)
  \(\nabla_\beta\left\| y - X\beta\right\|_2 = (\partial_{\beta_1}\left\| y - X\beta\right\|_2,\dots,\partial_{\beta_d}\left\| y - X\beta\right\|_2)\\ \partial_{\beta_k}\left\| y - X\beta\right\|_2 = \partial_{\beta_k}\left\{\frac{1}n\sum_{i=1}^n{\left(y_i - \sum_{j=1}^{d}X_{ij}\beta_j\right)^2}\right\}^\frac{1}2 = -\frac{X^T_{\cdot k}(y - X\beta)}{n\left\| y - X\beta\right\|_2}\\ X^T_{\cdot k} = 행렬\ X의\ k번째\ 열(column)\ 벡터를\ 전치시킨\ 것\\ 즉,\\ \nabla_\beta\left\| y - X\beta\right\|_2 = (\partial_{\beta_1}\left\| y - X\beta\right\|_2,\dots,\partial_{\beta_d}\left\| y - X\beta\right\|_2) = \left( -\frac{X^T_{\cdot 1}(y - X\beta)}{n\left\| y - X\beta\right\|_2},\dots, -\frac{X^T_{\cdot d}(y - X\beta)}{n\left\| y - X\beta\right\|_2}\right)\)

• 이에 목적식을 최소화하는 β를 구하는 경사하강법 알고리즘은 다음과 같다.

\[\beta^{(t+1)}\leftarrow\beta^{(t)} - \lambda\nabla_\beta\left\| y - X\beta\right\|_2 =\beta^{(t)} + \frac{\lambda}n\frac{X^T(y - X\beta^{(t)})}{\left\| y - X\beta\right\|_2}\\\]

• 목적식으로 ∥y-Xβ∥~2~ 대신 ∥y-Xβ∥~2~^2^을 최소화하면 식이 좀더 간단해진다.

\[\nabla_\beta\left\| y - X\beta\right\|_{2}^2 = (\partial_{\beta_1}\left\| y - X\beta\right\|_{2}^2,\dots,\partial_{\beta_d}\left\| y - X\beta\right\|_{2}^2) = -\frac{2}nX^T(y - X\beta) \\ \beta^{(t+1)}\leftarrow\beta^{(t)} + \frac{2\lambda}{n}X^T(y - X\beta^{(t)})\]

경사하강법 기반 선형회귀 알고리즘 슈도 코드

Input: X, y, lr, T, Output: beta
# norm: L2-노름을 계산하는 함수
# lr: 학습률, T: 학습횟수 = hyperparameter
for t in range(T):  # 학습횟수 제한, 또는 이전 처럼 일정한 수준 이하로 떨어질 때까지 해도 된다.
    error = y - X @ beta
    grad = - transpose(X) @ error
    beta = beta - lr * grad # 베타 업그레이드

확률적 경사하강법 (stochastic gradient descent)

• 이론적으로 적절한 학습률과 학습횟수를 선택시, 수렴이 보장되어있다.

• 하지만 비선형회귀의 경우 목적식이 볼록하지 않으므로(non-convex) 수렴이 항상 보장되지 않음

  • 딥러닝의 목적식은 대부분 볼록함수가 아니다, 즉 대부분 보장하지 않음
  • 아래와 같은 경우 특정 부분에 수렴했지만 함수의 최소지점이 아니다.

  

​

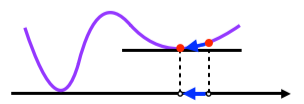
• 확률적 경사하강법(SGD)은 모든 데이터를 사용해서 업데이트 하는 대신 데이터 한개 또는 일부활용하여 업데이트합니다.

  가정

  

\[\theta^{(t+1)}\leftarrow\theta^{(t)}-\widehat{\nabla _{a}L}(\theta^{(t)})\]

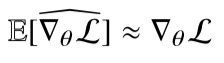
• 만능은 아니지만 딥러닝에서 mini-batch 방식을 추가하여 일반적으로 사용함.
• SGD는 데이터의 일부를 가지고 패러미터를 업데이트하기 때문에 연산자원을 좀 더 효율적으로 활용
  • 연산량이 b/n으로 감소

\[\beta^{(t+1)}\leftarrow\beta^{(t)} + \frac{2\lambda}{b}X^T_{(B)}(y_{(b)} - X_{(b)}\beta^{(t)})\]

• 경사하강법은 전체 데이터를 가지고 목적식 그레디언트 벡터를 계산하는 반면, SGD는 미치배치(데이터의 일부)를 가지고 그레디언트 벡터를 계산

• 그러므로 매번 다른 데이터셋을 사용하는 것과 비슷하기 때문에 함수 곡선의 모양이 미니배치마다 바뀌게 된다.

• 하지만 최종적인 방향성은 유사하게 이동하게 된다.

  

• 즉 볼록모양이 아니어도 효율적으로 활용가능 하다.

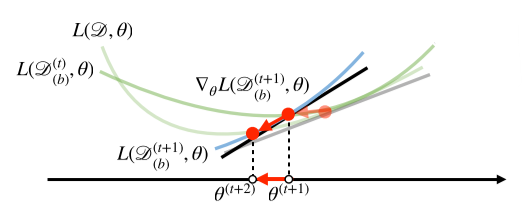
경사하강법(좌) vs 확률적 경사하강법(우)

• 다만 mini-batch 사이즈를 너무 작게 잡으면 경사하강법에 비해 너무 느려진다.

• 최근에는 경사하강법으로 전체 데이터를 이용해 학습시키면, 방대한 데이터셋에 의하여 메모리가 초과되므로 미니배치로 나누어서 학습하는 SGD를 사용한다.

인공지능 학습의 수학적 이해

신경망의 해석

• 비선형, 복잡한 모델이 대부분인 신경망은 사실 선형 모델과 비선형 함수들의 결합으로 이루어져 있다.

\[\begin{aligned}\begin{aligned}\begin{bmatrix} O_1 \\ O_2 \\ \vdots \\ O_n \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \begin{bmatrix} w_{11} & w_{12} & \dots & w_{1p}\\ w_{21} & w_{22} & \dots & w_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ w_{d1} & w_{d2} & \dots & w_{dp} \end{bmatrix} + \begin{bmatrix} \vdots&\vdots&\ddots&\vdots\\b_1&b_2&\dots&b_p \\ b_1&b_2&\dots&b_p \\ b_1&b_2&\dots&b_p\\\vdots&\vdots&\ddots&\vdots\end{bmatrix}\\ O\ \ \ \ \ \ \ \ \ \ \ \ \ \ X\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ W \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b\ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{aligned}\\(n \times p)\ \ \ \ (n \times d)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (d\times p)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (n\times p) \ \ \ \ \ \ \ \ \ \end{aligned}\]

[math 0. 신경망 수식 분해]

• b는 각 한 행의 모든 값이 같다.

으에에... 이게 머야 언젠간 고치기
graph BT
	x1((x<sub>1</sub>)) & x2((x<sub>2</sub>)) & x((x...)) & xd((x<sub>d</sub>))-->o1((O<sub>1</sub>)) & os((o...)) & op((O<sub>p</sub>))

[chart 0. 신경망 모델의 차트화]

• d개의 변수로 p개의 선형모델을 만들어 p개의 잠재변수를 설명하는 모델의 도식화이다.

• 화살표는 w~ij~들의 곱을 의미한다.

소프트맥스 연산

\[softmax(o) = softmax(Wx+b) = \left( \dfrac{\exp(0)}{\sum_{k=1}^p\exp(o_k) }, \dots, \dfrac{\exp(0_p)}{\sum_{k=1}^p\exp(o_k) },\right)\]

[math1.softmax]

• 소프트맥스(softmax) 함수는 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
• 분류 문제를 풀 때 선형모델과 소프트 맥스 함수를 결합하여 예측

def softmax(vec):
    denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True)) # 각 출력의 값
    # 너무 큰 벡터가 들어오는 것을 막기위해 np.max(vec)을 vec에서 빼서 방지
    numerator = np.sum(denumerator, axis=-1, keepdims=True)#모든 출력의 값들의 합
    val = denumerator / numerator
    return val

[code 1.softmax의 코드 구현]

• 이러한 소프트맥스 함수로 벡터를 확률 벡터(각 성분의 합이 1인 벡터)로 변환할 수 있다.

def one_hot(val, dim):
    return [np.eye(dim)[_] for _ in val]
def one_hot_encoding(vec):
    vec_dim = vec.shape[1]
    vec_argmax= np.argmax(vec, axis=-1)
    return one_hot(vec_argmax, vec_dim)

[code 1-1.one_hot 함수 구현]

• 학습이 아닌 추론시에는 one_hot 벡터를 이용해 가장 큰 벡터를 정답으로 삼으면 되므로 softmax()를 씌울 필요 없다.(one_hot(softmax(o)=> X, one_hot(o) => O)

활성화 함수(activation function)와 다층 신경망(MLP)

• 신경망은 선형모델과 활성함수(activation function)을 합성한 함수

\[H = (\sigma (z_1), \dots, \sigma(z_n)), \sigma(z) = \sigma(Wx + b)\\ \sigma = 활성함수(비선형),\ z = (z_1,\dots,z_q) = 잠재벡터,\ H = 새로운\ 잠재벡터 = 뉴런\]

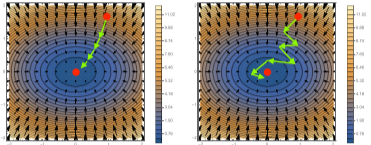
[math 2. 신경망 뉴런]

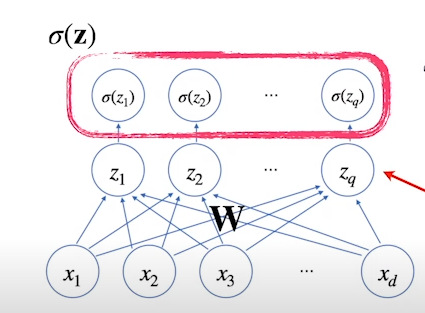
[img 2. 신경망 뉴런 도식화]

• 잠재벡터들을 이용해 만든 새로운 잠재벡터들,(그리고, 이 새로 만든 잠재벡터로 만들 새로운 잠재벡터들)을 뉴런(neuron) 또는 이라고 하며, 이러한 구조의 인공신경망을 퍼셉트론(perceptron)이라고 한다.
  • 각 뉴런(노드) 가 가지고 있는 값은 텐서(tensor)라고 한다.
• 활성화 함수는 실수값을 받아 실수값을 돌려주는 비선형(nonlinear) 함수
  • 비선현 근사를 하기 위해 존재
• 이로 인해 딥러닝이 선형모형과 차이를 보였으며, 시그모이드(sigmoid), $tanh$, 그리고 주로 쓰이고 있는 ReLU 함수 등이 있다.

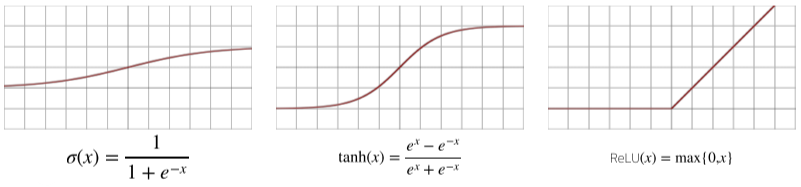
[img 3. sigmoid, tanh, ReLu 함수 그래프]

• 만약, 이렇게 구한 잠재 벡터 H에서 가중치행렬 $W^{(2)}$와 $b^{(2)}$를 통해 다시 한번 선형 변환해서 출력하게 되면 ($W^{(2)}, W^{(1)}$)를 패러미터로 가진 2층(2-layers) 신경망이 된다.

\[O = H W^{(2)} + b^{(2)},\ H = (\sigma (z_1), \dots, \sigma(z_n)) = \sigma( Z^{(1)}),\ \sigma(z) = \sigma(W^{(1)}x + b^{(1)}) \\ Z^{(1)} = X W^{(1)} + b^{(1)}\]

[math 2-1. 2중 신경망]

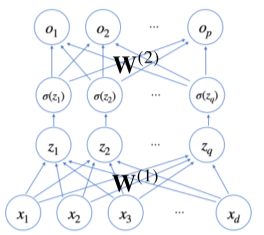
[img 2-1.2중 신경망의 구조]

• 이렇게 신경망이 여러층 합성된 함수를 다층(multi-layer) 퍼셉트론(MLP)라고 한다.

\[\\ O = Z^{(L)} \\ \vdots \\ H^{(l)} = \sigma(Z^{(l)}) \\ Z^{(l)} = H^{(l-1)} W^{(l)} + b^{(l)} \\ \vdots \\{H^{(1)}} = \sigma(\bold Z^{(1)}) \\ Z^{(1)} = X\bold W^{(1)} + b^{(1)}\]

[math 2-2. n층으로 이루어진 다중신경망의 합성함수]

• $l = 1,\dots,L$까지 순차적인 신경망 계산을 순전파(forward propagation)이라 부른다.

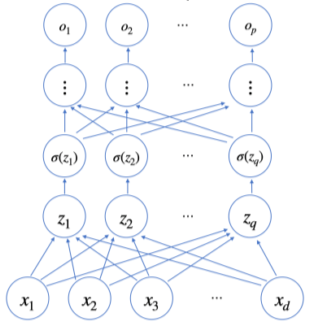
[img 2-3. 다층 신경망 구조]

• 이론적으로 2층 정도의 신경망으로도 임의의 연속함수를 근사(universal approximation theorem)할 수 있다.
• 층이 깊을 수록 필요한 뉴런(텐서를 가지고 있는 노드), 파라미터의 숫자가 기하급수적으로 줄어들어 좀 더 효율적이다.
  • 즉, 층을 깊이 하면 넓이를 얇게 해도 된다.
  • 물론 최적화는 여전히 어렵다.(CNN에서 깊게 설명)

역전파(backpropagation) 알고리즘

• 각 층에 사용된 패러미터 ${W^{l},b^{l}}^L_{l=1}$을 역순으로 학습하는데 사용된다.
• 합성미분의 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)을 이용하여 역순으로 구한다.

\[z = (x+y)^2의\ 그레디언트\ 벡터,\ \dfrac{\partial z}{\partial x} =\ ?\\ z = w^2 \rightarrow \dfrac{\partial z}{\partial w} = 2w w = x + y \rightarrow \dfrac{\partial w}{\partial x} = 1,\ \dfrac{\partial w}{\partial y} = 1\\ \dfrac{\partial z}{\partial x} = \dfrac{\partial z}{\partial w}\dfrac{\partial w}{\partial x} = 2w \cdot 1 = 2(x+y)\]

[math 3. 편미분을 이용한 역전파 알고리즘 예시]

• 먼저 윗층의 그레디언트 벡터를 구한 뒤, 그 벡터를 이용해 그 아래 그레디언트 벡터를 구한다.
  • 포워드 프로파 게이션과 달리, 각 뉴런 또는 노드의 텐서 값을 메모리에 넣어야 하므로, 메모리를 많이 먹는다.

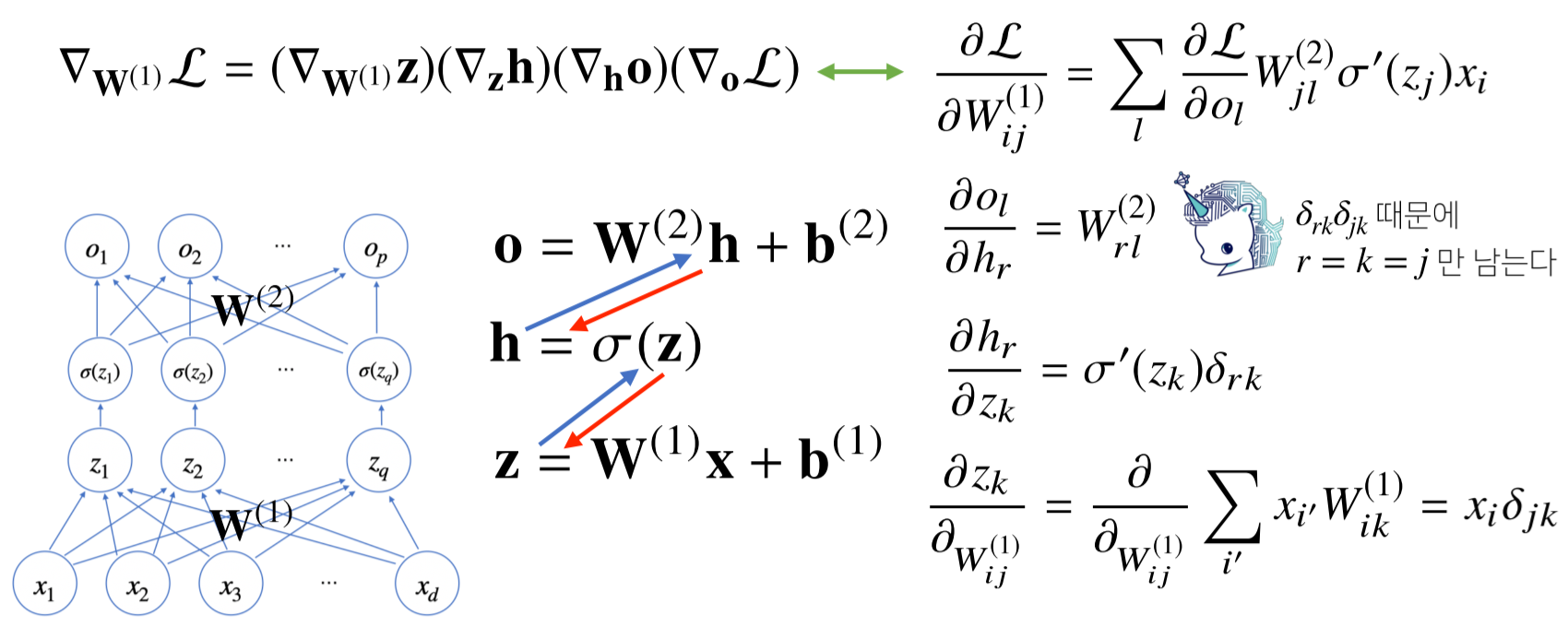
[img 3. 2층 신경망 어려운 예제]

• 파란색 : forward propagation
• 빨간색 : back propagation

확률론

• 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있으며, 통계적 해석은 손실함수 들의 기본 작동원리이다.
  • 회귀 분석의 L2 노름은 예측오차 분산을 최소화하는 방향으로 학습하며
  • 분류 문제의 교차 엔트로피는 모델 예측의 불확실성을 최소화하는 방향으로 학습한다.

확률분포

• 확률분포란, 확률 변수가 특정한 값을 가질 확률을 나타내는 함수를 의미한다.

• 확률분포는 데이터공간 $(x, y)$ 에서 데이터를 추출하는 분포이다.

• 확률 변수는 이산형(discrete)과 연속형(continuous)으로 구분된다.

  • 이산형 확률 변수 : 확률 변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해 모델링
    \(\mathbb{P}(X \in A) = \sum_{x\in A}{P(X= x)}\\ \mathbb{P} = 확률변수\)

  [math 4. 이산형 확률변수]

  • 연속형 확률 변수 : 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링한다.
  \[\mathbb{P}(X \in A) = \int_{A}{P(x)dx}\\ P(x)=\lim_{h\rightarrow0}\frac{\mathbb{P}(x - h \leq X \leq x + h)}{2h}= 확률변수의\ 밀도\]

  [math 4-1. 연속형 확률변수]

• $P(x)$는 입력 x에 대한 주변확률 분포로 y에 대한 정보를 주진 않음

기대값

• 조건부 확률 $P(x|y)$는 데이터 공간에서 입력 x와 출력 y 사이의 관계를 모델링하며, 입력 변수 x에 대해 정답이 y일 확률을 의미함.

• $softmax(W\phi + b )$은 데이터 x으로부터 추출된 특징패턴 $\phi (x)$과 가중치행렬 W을 통해 조건부확률 $P(y|x)$을 계산

• 기대값(expectation)은 데이터를 대표하는 통계량, 확률 분포를 통해 다른 통계적 범함수를 계산하는데 사용

  • 회귀 문제의 경우 조건부 기대값을 추정하며 이는 각 확률분포에 따라 다음과 같이 구한다.
  \[\mathbb{E}_{x\sim P(x)}[f(x)] = \int_\chi f(x)P(x)dx \rightarrow연속확률분포\ \ \\ \mathbb{E}_{x\sim P(x)}[f(x)] = \sum_{x\in\chi} f(x)P(x) \rightarrow 이산확률분포\]

  [math 5. 기대값 구하기]

  • 분산, 첨도 공분산 등의 통계량을 계산하는데 사용함.

\[분산 : \mathbb{V}(x) = \mathbb{E}_{x\sim P(x)}[(x-\mathbb{E}[x])^2]\\ 비대칭도 : Skewness(x) = \mathbb{E}\left[\left(\frac{x-\mathbb{E}[x]}{\sqrt{\mathbb{V}(x)}}\right)^3\right]\\ 공분산 : Cov(x_1,x_2) = \mathbb{E}_{x_1,x_2\sim P(x_1,x_2)}(x_1 -\mathbb{E}[x_1])(x_2 - \mathbb{E}[x_2])\]

​ [math 5-1. 기대값의 사용]

몬테카를로 샘플링(Monte Carlo sampling)

• 확률 분포를 모를 때 데이터를 이용하여 기대값을 계산하는 방법.
• 이산형, 연속형이든 관계없이 다음과 같이 표현함.

\[\mathbb{E}_{x\sim P(x)}[f(x)] \approx \frac{1}{N}\sum^N_{i=1}f(x^{(i)}),\ x^{(i)}\stackrel{\text{i.i.d.}}{\sim} P(x)\]

[math 6.몬테카를로 샘플링]

• 독립 추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렴성을 보장

import numpy as np
#f(x) = e^(-x^2), [-1, 1]
def mc_int(fun, low, high, sample_size=100, repeat=10):
    int_len = np.abs(high - low)
    stat = []
    for _ in range(repeat):
        x = np.random.uniform(low=low, high=high, size=sample_size)
        fun_x = fun(x)
        int_val = int_len * np.mean(fun_x)
        stat.append(int_val)
    return np.mean(stat), np.std(stat)

def f_x(x):
    return np.exp(-x**2)

print(mc_int(f_x, low=-1, hight=1, sample_size=10000, repeat=100))

[code 6. f(x), [-1, 1] 몬테카를로 코드구현]

통계학

• 통계적 모델링은 적절한 가정 위에서 확률 분포를 추정(inference)하는 것이 목표이며, 이는 기계학습이 결과를 예측하는 것과 같은 목표이다.
• 유한한 개수의 데이터로는 모집단의 분포를 정확하게 알아낼 수 없으므로 근사적으로 확률분포를 추정하여 불확실성을 최소화

모수

• 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametirc) 방법론이라고 함.
  • 이와 반대로 데이터에 따라 모델의 주조 및 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라 부르며 기계학습의 많은 방범론이 이를 따르기도 함.

데이터 모수 추정

확률 분포 가정

• 히스토그램의 모양을 관찰하여 확률분포를 가정할 수 도 있다.

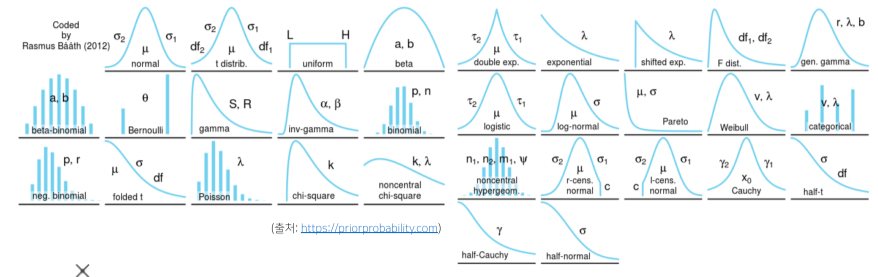
[img 7. 여러가지 모양의 확률 분포]

확률 분포명	데이터 모양
베르누이 분포	데이터가 2개의 값(0 또는 1)만 가짐
카테고리 분포	데이터가 n개의 이산적인 값만을 가짐
베타 분포	데이터가 [0, 1] 사이에서 값을 가짐
감마 분포, 로그 정규 분포	데이터가 0 이상의 값을 가짐
정규 분포, 라플라스 분포	데이터가 $\mathbb{R}$(실수) 전체에서 값을 가짐

[fig 7. 확률 분포의 예시]

• 하지만 이런식으로 가정하는 것보다 데이터를 생성하는 원리를 고려한 뒤, 각 분포마다 모수를 추정 후 각 확률분포의 검정방벙으로 검정하는 방식이 원칙이다.

데이터 모수 추정

• 데이터 확률분포를 가정한 수 데이터 모수를 추정한다.

• 평균 $\mu$와 분산 $\sigma^2$으로 이를 추정하는 통계량(statistic)은 다음과 같다.
  \(\stackrel{표본 평균}{\bar{X} = \frac{1}{N}\sum^N_{i=1}X_i},\ \ \ \stackrel{표본 분산}{S^2 = \frac{1}{N-1}\sum^N_{i=1}(X_i-\bar{X})^2}\\ \mathbb{E}[\bar{X}] = \mu,\ \ \ \mathbb{E}[S^2] = \sigma^2,\ 표본 표준 편차 = \sqrt{표본분산} = \sqrt{S^2} = S\)
  [math 7. 통계량 계산]

  • 표본분산을 구할 때 N이 아닌 N-1로 나누는 이유는 불편(unbiased) 추정량을 구하기 위해서라고 하며, 고급 통계학 내용이므로 일단 넘어가겠다.

• 통계량의 확률 분포를 표집분포(Sampling distribution)이라 부르며, 특히 표본평균의 표집분포는 N이 커질수록 정규분포 $\mathcal{N}(\mu,\sigma^2/N )$를 따릅니다.

  • 이를 중심 극한 정리(Central Limit Theorem)이라 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립합니다.

최대 가능도(maximum likelihood estimation, MLE) 추정

• 통계량을 측정하는 적절한 방법은 확률분포마다 다르다.

• 이론적으로 가장 가능성이 높은 모수 측정 방법은 최대 가능도 추정법(maximum likelihood estimation, MLE)입니다.
  \(\hat{\theta}_{MLE} = argmax\ L(\theta;x) = argmax\ P(x|\theta)\)
  [math 8. 최대가능도 추정법]

• 데이터 집합 X가 독립적으로 추출되었을 경우 로그가능도를 최적화합니다.

  • 이때 모수 $\theta$는 가능도를 최적화하는 MLE가 됩니다.

\[L(\theta;X) = \prod^n_{i=1}P(x_i|\theta) \Rightarrow log\ L(\theta; X) = \sum^n_{i=1}logP(x_i|\theta)\]

​ [math 8. 독립 추출 시의 추정법 최대가능도 추정법]

• 데이터의 숫자가 수억단위가 되면 컴퓨터의 연산으로 계산 불가능하므로, 데이터가 독립일 시, 로그 가능도의 덧셈으로 바꾸면 컴퓨터로 연산이 가능해짐.
  • 경사하강법으로 가능도 최적화시, 미분연산을 사용하며, 음의 로그가능도(negative log-likelihood)를 사용하면 연산량이 O(n^2^)에서 O(n)으로 줄여준다.
  • 불편 추정량을 보장하진 않음.

최대 가능도 추정법 예제

정규분포

\[\hat{\theta}_{MLE}= argmax\ L(\theta; x) = argmax\ P(x|\theta)\\ log\ L(\theta;X) = \sum^n_{i=1}logP(x_i|\theta) = \sum^n_{i=1}log\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{{|x_i-\mu|^2}}{2\mu^2}} = -\frac{n}{2}log2\pi\sigma^2 - \sum^n_{i=1}\frac{{|x_i-\mu|}^2}{2\sigma^2}\]

[math 8-1. 모수 추정을 위한 로그 가능도 계산]
\(0 = \frac{\partial logL}{\partial\mu}= -\sum^n_{i=1}\frac{x_i - \mu}{\sigma^2} \Rightarrow \hat{\mu}_{MLE}=\frac{1}{n}\sum^N_{i=1}x_i\\ 0 = \frac{\partial logL}{\partial\sigma}= -\frac{n}{\sigma}+\frac{1}{\sigma^3}\sum^n_{i=1}|{x_i - \mu}|^2 \Rightarrow \hat{\sigma}_{MLE}^2=\frac{1}{n}\sum^N_{i=1}(x_i -\mu)^2\\\)
[math 8-2. 미분을 통한 모수 추정]

카테고리 분포

\[\hat{\theta}_{MLE}= argmax\ P(x_i|\theta) = argmax\ log(\prod^n_{i=1}\prod^d_{k=1}p_k^{x_i,k})\\ log(\prod^n_{i=1}\prod^d_{k=1}p_k^{x_i,k})=\sum^d_{k=1}(\sum^n_{i=1}x_{i,k})logp_k = \sum^d_{k=1}n_klogp_k\ with\ \sum^d_{k=1}p_k=1\\ \Rightarrow \mathcal{L}(p_1,\dots,p_k,\lambda) = \sum^d_{k=1}n_k logp_k + \lambda(1-\sum_kp_k) (라그랑주\ 승수법)\\ 0 = \frac{\partial \mathcal{L}}{\partial p_k} = \frac{n_k}{p_k} - \lambda,\ \ \ 0=\frac{\partial \mathcal{L}}{\partial \lambda} = 1 - \sum^d_{k=1}p_k \rightarrow\ p_k =\frac{n_k}{\sum^d_{k=1}n_k}\]

**[math 8-3. 모수 추정] **

딥 러닝에서 최대가능도 추정법

• 딥러닝 모델의 가중치를 $\theta=(W^{(1)},\dots,W^{(L)})$라 표기했을 때 분류 문제에서 소프트맥스 벡터는 카테고리 분포의 모수 $(p_1,\dots,p_k)$를 모델링합니다.

• 원핫벡터로 표현한 정답레이블 $y= (y_1, \dots,y_k)$을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화할 수 있습니다.
  \(\hat{\theta}_{MLE} = argmax \frac{1}{n}\sum^n_{i=1}\sum^K_{k=1}y_{i,k}log(MLP_\theta(x_i)_k)\)
  [math 9. 분류 문제 최대가능도 추정]

확률분포의 거리 구하기 - 쿨백-라이블러 발산

• 기계학습에서 사용되는 함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도됩니다.
• 두 개의 확률분포 P(x), Q(x)가 있을 경우 두 확률분포 사이의 거리(distance)를 계산할 때 여러 함수를 이용
  • 총변동 거리 (Total Variation Distance, TV)
  • 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)
  • 바슈타인 거리 (Wasserstein Distance)
• 이 중 쿨백-라이블러 발산(KL Divergence)은 다음과 같이 정의.
  \(\mathbb{KL}(P\|Q) = -\mathbb{E}_{x\sim P(x)}[logQ(x)] + \mathbb{E}_{x\sim P(x)}[logP(x)]\\ -\mathbb{E}_{x\sim P(x)}[logQ(x)] = 크로스\ 엔트로피,\ \mathbb{E}_{x\sim P(x)}[logP(x)] = 엔트로피\)

[math 10. 쿨백-라이블러 발산 구하기]

• 분류 문제에서 정답레이블을 P, 모델 예측을 Q라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화 하는 것과 같음.

베이즈 통계학

• 베이즈 통계학이란, 모수 추정에 사용되는 베이즈 정리에 대한 내용, 데이터 추가시 데이터 업데이트 방법에 대한 이론
• 베이즈 정리란, 조건부확률을 이용해 정보를 갱신하는 방법을 알려줌, 예측 모형의 방법론

조건부 확률

• 조건부 확률 $P(A|B)$는 사건 B가 일어난 상황에서 사건 A가 발생할 확률
• 이를 통해 $P(A|B)$ 또한 구할 수 있다.

\[P(A\cap B) = P(B)P(A\|B)\\ P(B\|A) = \frac {P(A\cap B)}{P(A)} = P(B)\frac {P(A\|B)}{P(A)}\]

[math 11. 조건부확률에 대한 식]
\(P(\theta\|\mathcal{D}) = P(\theta)\frac{P(\mathcal{D}\|\theta)}{P(\mathcal{D})}\\ P(\theta\|\mathcal{D}) : 사후확률(posterior),\ P(\theta):사전확률(prior), \ P(\mathcal{D}|\theta): 가능도(likelihood),\ P(\mathcal{D}):Evidence\)
[math 11-1. 베이즈 정리 용어 정리]

• 예시를 들어보자면 코로나 발병률이 10%(사전확률 $P(\theta)$:0.1), 실제로 걸려서 확진될 확률 99%, 안걸렸는데 오진될 확률 1% (가능도, $P(\mathcal{D}|\theta)$: 0.99, 0.01 )라 할때 질병에 걸린 사람의 검진결과가 나왔을 때 정말로 코로나에 감염되었을 확률?

\[P(\theta) = 0.1,\ P(\neg\theta) = 0.9,\ P(\mathcal{D}\|\theta)=0.99,\ p(\mathcal{D}\|\neg\theta)=0.01\\ P(\mathcal{D}) = \sum_\theta P(\mathcal{D}\|\theta)P(\theta) = 0.99 \times 0.1 + 0.01 \times0.9 = 0.108\\ P(\theta\|\mathcal{D}) = 0.1 \times\frac{0.99}{0.108} \approx 0.916 \rightarrow 정답\]

[math 11-2. 사후확률 계산]

• $\theta : 코로나\ 발병사건으로\ 정의(관찰 불가),\ \mathcal{D}: 테스트\ 결과로\ 정의(관찰 가능), \neg\theta : ~가\ 아닐\ 확률$
• 오탐율(False alarm)이 오르면 테스트의 정밀도(Precision)가 떨어진다. (0.1로 10배 오를시 0.524까지 떨어짐)

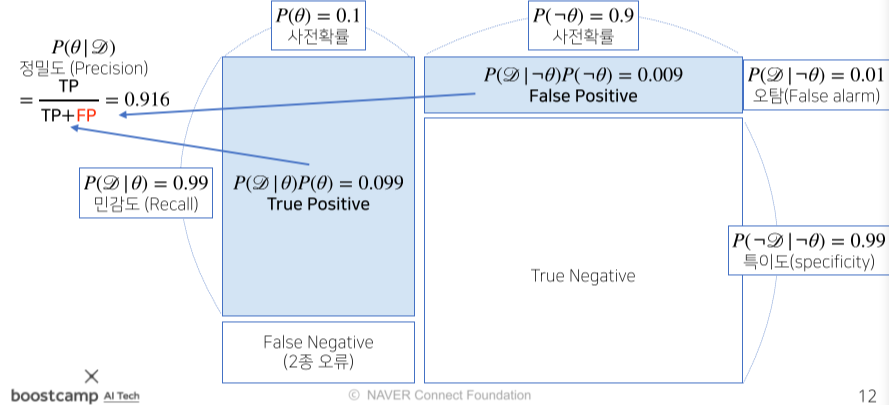
[img 11. 조건부 확률의 시각화]

베이즈 정리를 통한 정보의 갱신

• 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있음.

\[new\ P(\theta\|\mathcal{D}) = P(\theta\|\mathcal{D})\frac{P(\mathcal{D}\|\theta)}{P(\mathcal{D})}\]

[math 12. 갱신된 사후확률 구하기]
\(new\ P(\theta\|\mathcal{D}) = 0.1 \times \frac {0.99}{0.189} \approx 0.524,\ P(\theta\|\mathcal{D}) = 0.99,\ P(\theta\|\neg\mathcal{D}) = 0.1 \\ P(\mathcal{D}^*)=0.99\times0.524+0.1\times0.476 \approx0.566\\ 갱신된\ 사후확률\ P(\theta\|\mathcal{D}^*) = 0.524 \times\frac{0.99}{0.566}\approx0.917\)
[math 12-1. 갱신된 사후확률 계산]

• 코로나 확정을 받은 사람이 오진율이 10%일시 두번째 검진이 양성일 시에도 확진일 확률?

조건부확률과 인과관계의 차이

• 데이터가 많아도 조건부 확률은 인과관계(causality)와 다르다

• 인과관계는 데이터 분포의 변화에 강건한 예측 모형을 만들 때 고려함.
  • 인과 관계를 고려하지 않으면 시나리오나 바뀐 데이터에 따라 정확도가 크게 떨어짐
• 인과관계는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산 해야함.
  • 키가 클수록 지능지수가 높다? => 연령이 클수록 나이와 지능이 높아서 생기는 인과관계
  • 여기서 중첩요인은 연령

simpson’s paradox에 의한 인과관계 오류

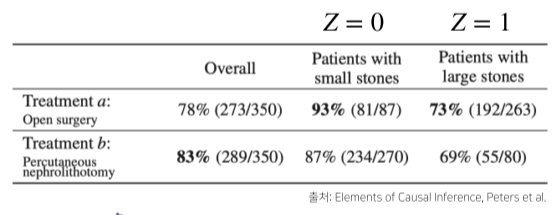
[img 13. 신장 결석 치료법에 따른 치료율]

• 실제로는 작은 결석 또, 큰 결석 관계없이 외과수술이 치료율이 높지만, 약물 치료법이 성공율이 높은 작은 결석 치료에 많이 사용되므로 전체 치료율은 높아보인다.
• do(T=a)라는 조정 효과를 통해 Z의 개입을 제거해야한다.

\[P_a(R=1) = \sum_{z\in \{0,1\}}P(R=1\|T=b,Z=z)P(Z=z) = \frac{81}{87}\times\frac{(87+270)}{700} + \frac{192}{263}\times\frac{263+80}{700}\approx 0.8325 \\ P_b(R=1) = \sum_{z\in \{0,1\}}P(R=1\|T=b,Z=z)P(Z=z) = \frac{234}{270}\times\frac{(87+270)}{700} + \frac{55}{80}\times\frac{263+80}{700}\approx 0.7789\]

[math 13. 조정 효과를 통한 Z(중첩요인) 개입 제거]

CNN

CNN(Convolution Neural Network)의 이해

• 기존의 모델들은 뉴런이 모두 연결된 (fully connected) 구조였지만 CNN은 동일한 고정된 가중치 값을 가진 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조임.
• 선형의 변환의 한 종류임은 같음,
• 커널 사이즈는 고정되므로 parameter 사이즈가 작다.

\[h_i =\sigma\left(\sum^k_{j=1}V_jx_{i+j-1}\right)\]

[math 14. Convolution 연산]

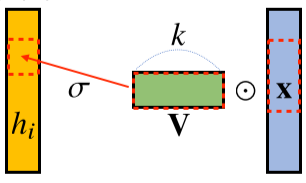
[img 14. Convolution 연산 그림]

• CNN의 수학적 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜 정보를 추출 또는 필터링하는 것이며, 이는 크게 2가지 정의 할 수 있다.
  • 정의역이 연속적(continuous)인 공간 : 적분으로 표현
  • 정의역이 이상(discrete) 공간 : 급수로 표현

\[continuous\ \ \[f*g\]\(x\) = \int_{\mathbb{R}^d}f(z)g(x-z)dz=\int_{\mathbb{R}^d}f(x-z)g(z)dz=\[g*f\]\(x\)\\ discrete\ \ \[f*g\]\(i\) = \sum_{a \in \mathbb{Z}^d}f(a)g(i-a)=\sum_{a \in \mathbb{Z}^d}f(i-a)g(a)=\[g*f\]\(i\) \\ g(x-z), g(i-a) : signal\ term,\ f(z), f(a): kernal\ term\]

[math 14-1. Convolution 연산 수식]

• z 또는 a만 움직이는 형태로 연산
• 사실 x-z, i-a가아니라 x+z, i+a 이며 cross-correlation 이다.
  • 전체 공간에서는 +,-가 차이가 크지않으므로 convolution이라 불러왔음

Convolution 연산 그래픽적 이해

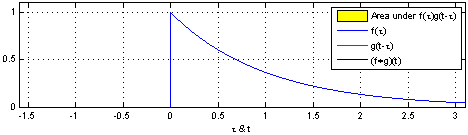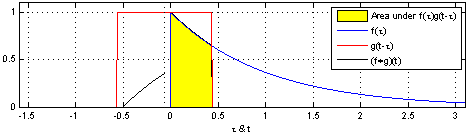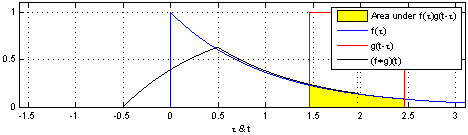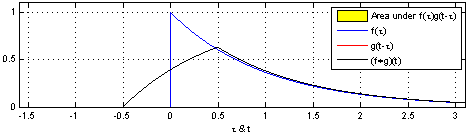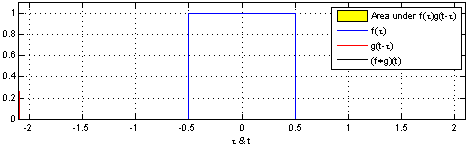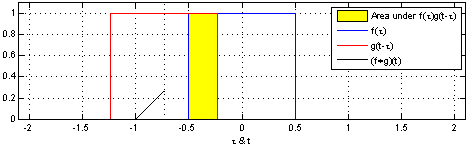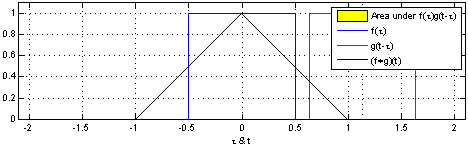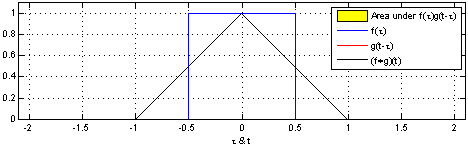[fig 14-1. Convolution 연산 그래픽적 이해]

• 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)로 적용.

\[1D-conv\ \ \[f*g\]\(i\) = \sum^d_{p=1}f(p)g(i+p)\\ 2D-conv\ \ \[f*g\]\(i,j\) = \sum_{p,q}f(p,q)g(i+p, j+q)\\ 3D-conv\ \ \[f*g\]\(i,j,k\) = \sum_{p,q,r}f(p,q,r)g(i+p, j+q, k+r)\\\]

[math 14-2. Convolution 여러 차원 연산]

• 1차원 뿐만 아니라 다양한 차원에서 계산 가능
• 1차원(text), 2차원(흑백), 3차원(컬러)별로 적용 가능
• 앞의 f항은 바뀌지 않는다.

다차원 CNN(Convolution Neural Network)의 이해

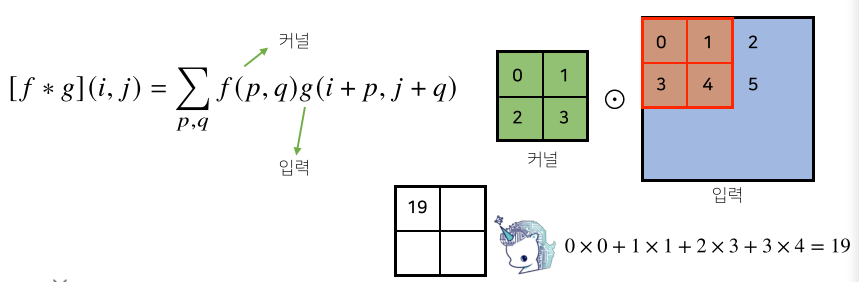
[img 14-2. 2차원 Convolution 연산 그래픽적 이해-1]

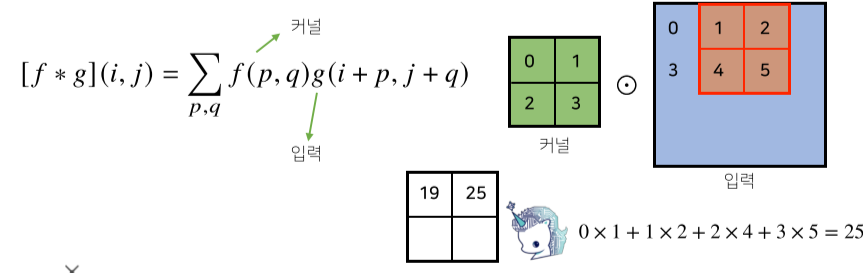
[img 14-3. 2차원 Convolution 연산 그래픽적 이해-2]
\(O_H=H-K_H+1\\ O_W=W-K_w+1\)

[math 14-3. Convolution 출력 크기 계산]

• 예를 들어 28x28 입력을 3x3 커널로 연산시 26x26이 된다.

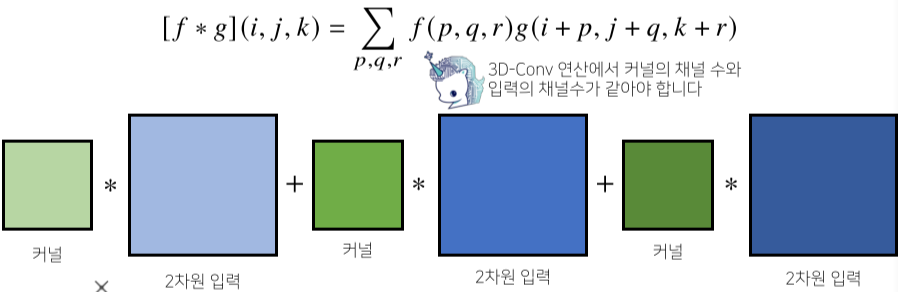
[img 14-4. 3차원 Convolution 연산 그래픽적 이해]

• 3차원의 경우 2차원 Convolution을 3번 적용하는 것이s다.
  • 커널의 갯수도 늘어남
• 3차원 부터는 입력을 텐서라고 말한다.

CNN의 역전파

• 커널이 모든 입력데이터에 공통으로 적용되므로 역전파 계산시 convolution 연산을 함

\[\frac \partial {\partial x}\[f*g\]\(x\) = \frac \partial {\partial x}\int_{\mathbb{R}^d}f(y)g(x-y)dy =\int_{\mathbb{R}^d}f(y)\frac {\partial g}{\partial x}(x-y)dy =\[f*g'\]\(x\)\]

[math 14-4. Convolution 연산 연속시 역전파]

• Discrete 구조에도 마찬가지로 성립한다.

\[\frac {\partial \mathcal{L}}{\partial w_i} = \sum_j \delta_jx_i+j-1, \\ ex) \frac {\partial \mathcal{L}}{\partial w_1}= \delta_ix_i + \delta_2x_2+\delta_3x_3\]

[math 14-5. Convolution 연산]

RNN

시퀀스(sequence) 데이터

• 소리, 문자열, 주가 추이 등, 순차적으로 들어오는 데이터
  • 시계열(time-series) 데이터는 시간 순서에 따라 나열된 데이터로, 시퀀스 데이터에 속함.
• 독립 동등 분포 ($i.i.d$)가정을 위배하기 때문에 순서를 바꾸거나 과거 정보이 변형되면 데이터의 확률 분포도 바뀜.
  • ex) 개가 사람을 물었다. $\leftrightarrow$ 사람이 개를 물었다. $\rightarrow$ 위치를 바꾼것 만으로, 데이터의 확률, 의미가 달라짐.

sequence data handling

• 이전 시퀀스의 정보로 앞으로의 데이터의 확률 분포를 다루기 위해 조건부확률 결합법칙 이용

\[P(X_1,\dots,X_t) = P(X_t\|X_1,\dots,X_{t-1})P(X_1,\dots,X_{t-1})\\ = P(X_t\|X_1,\dots,X_{t-1})P(X_{t-1}|X_1,\dots,X_{t-2})\times P(X_1,\dots,X_{t-2})\\ =\prod^t_{s=1}P(X_s\|X_{s-1},\dots,X_1)\\ \prod_{s=1}^t = s =1,\dots,t 까지\ 전부\ 곱하라\\ 즉,\ X_t \sim P(X_t\|X_{t-1},\dots,X_1), \\ X_{t+1} \sim P(x_{t+1}\|X_t,X_{t-1},\dots,X_1)\]

[math. 베이즈 법칙에 의한 P(X~s~) 추론 ]

• 과거 정보를 사용하지만 0부터 t-1까지 모든 데이터가 필요한건 아님, 오히려 지나친 과거 정보는 제외
  • 시퀀스 데이터를 다루기 위해선 길이가 가변적인 데이터를 다룰 수 있어야 한다.
  • 예를 들어, 시퀀스 데이터 $X_t$ 예측 시 전부가 아닌, $X_{t-1}\sim X_{t-\tau}$개 만큼만 사용하는 모델을 AR($\tau$), 즉 자기 회귀 모델(Autoregressive Model)이라고 부름.

• 위의 자기 회귀 모델의 경우 $\tau$를 파라메터로 하는데 이 값을 짐작하기 힘들거나 $\tau$ 이상의 과거 정보가 필요할지도 모른다.

  • 이를 보완하기 위한 모델이 잠재 자기 회귀 모델(Latent autoregressive Model, 잠재 AR 모델)이라고 부르며 RNN의 기본 모델이다.

\[X_t \sim P(X_t\|X_{t-1},H_t), \\ X_{t+1} \sim P(x_{t+1}\|X_t,X_{t-1},H_{t+1})\\ 잠재변수\ H_t=X_{t-2},\dots,X_{1}=Net_\theta(H_{t-1},X_{t-1})\]

[math. 잠재변수 H~t~를 신경망을 통해 반복 사용해 시퀀스 데이터의 패턴을 학습하는 것이 RNN]

RNN의 이해와 BPTT

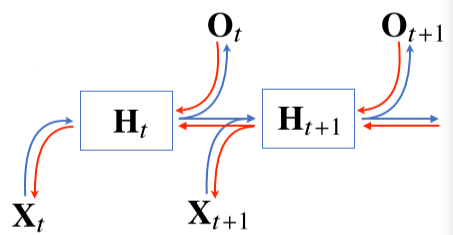
[img. 기본 RNN 모형, 순전파와 역전파 화살표 포함]

• 기본적인 RNN 모형은 Multi Layer Perceptron과 유사하다.
• 이전 순서의 잠재변수와 현재의 입력을 활용하여 모델링

\[O_t = HW^{(2)}+b^{(2)}\\ H_t = \sigma(X_tW_X^{(1)}+H_{t-1}W^{(1)}_H+b^{(1)})\\ O_t = 출력,\ H_t=잠재변수,\ \sigma=활성화함수,\ X_tW^{(1)}=가중치행렬,\ b^{(1)}=bias\\ O,H와\ 달리\ 가중치\ 행렬\ W\ 들은\ t(시간)에\ 따라\ 변하지\ 않음.\]

[math. 잠재변수 H~t~의 생성에서 이전 잠재변수인 H~t-1~ 활용]

• RNN의 역전파는 잠재변수의 연결 그래프에 따라 순차적으로 계산되며 이를 Backpropagtion Through Time(BPTT)라고 한다.

\(L(x,y,w_h,w_o)=\sum^T_{t=1}l(y_t,o_t)\\ \partial_{w_h}L(x,y,w_h,w_o)=\sum^T_{t=1}\partial_{w_h}l(y_t,o_t)=\sum^T_{t=1}\partial_{o_t}l(y_t,o_t)\part_{h_t}g(h_t,w_h)[\part_{w_h}h_t],\\ \part_{w_h}h_t=\part_{w_h}f(x_t,h_{t-1},w_h)+\sum^{t-1}_{i=1}\left(\prod^t_{j=t+1}\part_{h_{j-1}}f(x_j,h_{j-1},w_h)\right)\part_{w_h}f(x_i,h_{i-1},w_h)\\ while\ h_t=f(x_t,h_{t-1},w_h)\ and\ o_t =g(h_t,w_o).\)
[math. BPTT 역전파 계산 과정]

• RNN의 가중치행렬의 미분을 계산해보면 미분의 곱으로 이루어진 항이 계산됨.
  • 이 미분의 곱은 시퀀스의 길이가 길어질 수록 값이 불안정해진다.(무한대로 수렴 또는 0으로, 값이 크게 바뀜 등)
  • 이를 막기 위해 적절한 길이 시점에서 끊어 준다.(truncated BPTT 기술)

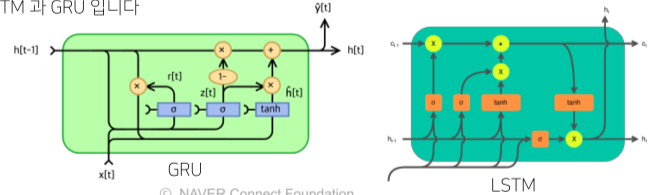
[img. LSTM과 GPU 그림]

• 최근에는 길이가 긴 시퀀스를 처리하기 위해 다른 RNN unit을 사용함.