풀스택 웹🌐 개발자 지망생 🧑🏽💻
➕ 인공지능 관심 🤖
Categories
-
┣
▶ COMPUTER_SCIENCE
📂: 7 -
┣
▶ WEB
📂: 3 -
┣
▶ ETC
📂: 3-
┃
┣
ETCS
📄: 10 -
┃
┣
SUBBRAIN 개발기
📄: 5 -
┃
┗
YOS 개발기
📄: 1
-
┃
┣
-
┗
▶ AI
📂: 9-
┣
AITOOLS
📄: 3 -
┣
CV
📄: 2 -
┣
DEEP_LEARNING
📄: 1 -
┣
DATA_VIS
📄: 2 -
┣
GRAPH
📄: 1 -
┣
LIGHTWEIGHT
📄: 1 -
┣
MATH
📄: 1 -
┣
NLP
📄: 3 -
┗
STRUCTURED_DATA
📄: 2
-
┣
모델 경량화 기본
- Lightweight model 개요
- 동전의 뒷면(The flip-side of the coin: on-device AI)
- 가장 적당하게 (Optimization)
- 모델의 시공간(Timespace of ML model)
- 압축
- Acceleration
- 가지치기(Pruning)
- 양자화 (Quantization for model compression)
- 지식 증류 (Knowledge distillation for network compression)
- 행렬 분해(Low-rank approximation for model compression)
모델 경량화(Lightweight) 기본
Naver AI boostcamp 내용을 정리하였습니다.
Lightweight model 개요
1. 결정 (Decision making)
연역적 (deductive) 결정
이미 참으로 증명(Axiom)되거나 정의를 통하여 논리를 입증하는 것
삼단 논법과 조합 $\begin{pmatrix}
n\r
\end{pmatrix}=\frac{n!}{r!(n-r)!}$ 증명 등이 있다.
- 삼단 논법 예시 : 소크라테스는 사람이다. 사람은 모두 죽는다. 소크라테스는 죽는다.
[math. 조합의 가정]
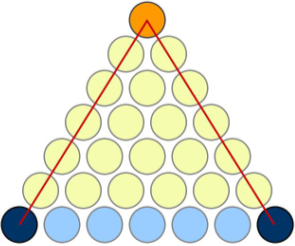
[img. 조합의 증명]
귀납적 (inductive) 결정
반복된 관찰과 사례를 통하여 논리를 입증
많은 통계학적 기법의 증명이 속한다.
예시: 몇만년동안 해는 동쪽에서 떠서 서쪽에서 진다 -> 고로 내일도 그럴 것이다.
단점으로, 100% 보장하지 않는다. (ex) 만약, 내일 태양이 폭발한다면?)
2. 결정기 (Decision making machine)
이전의 기계들은 사람이 결정을 하면 해당 결정의 목적 달성을 위해 도움을 주는 형태였다.
최근의 인공지능이 포함된 기기는 이때의 결정 또한 해주거나, 결정에 도움을 제공.
(ex) 공기질이 나빠지면 자동으로 켜지는 공기청정기)
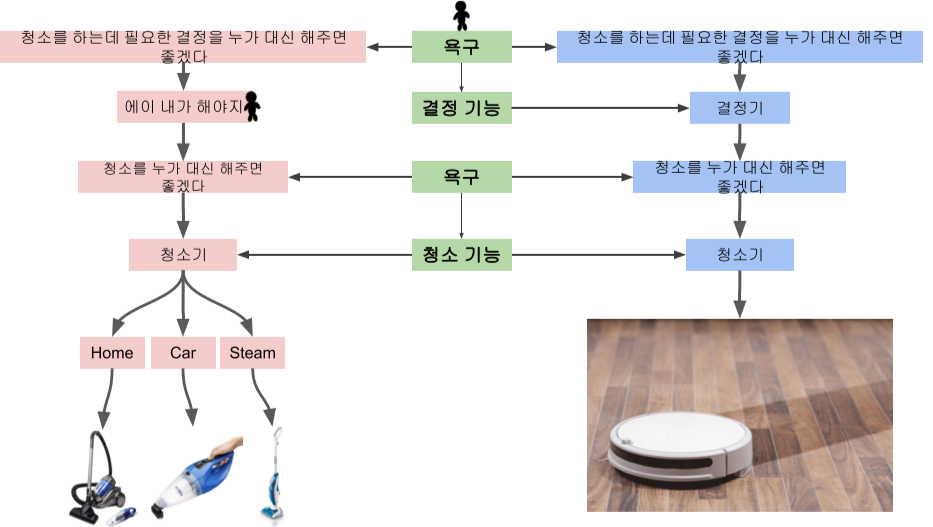
[img. 청소기를 예시로 든 결정기]
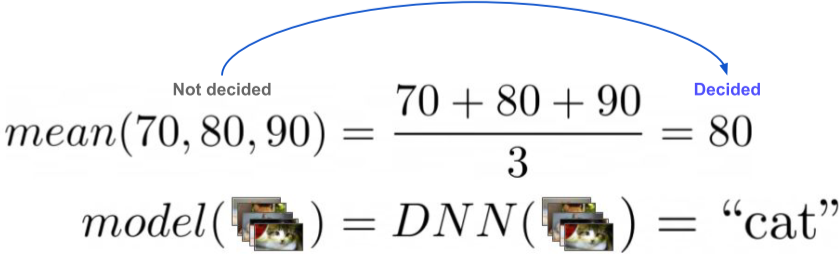
[img. 가장 간단한 통계학적 결정기인 평균]
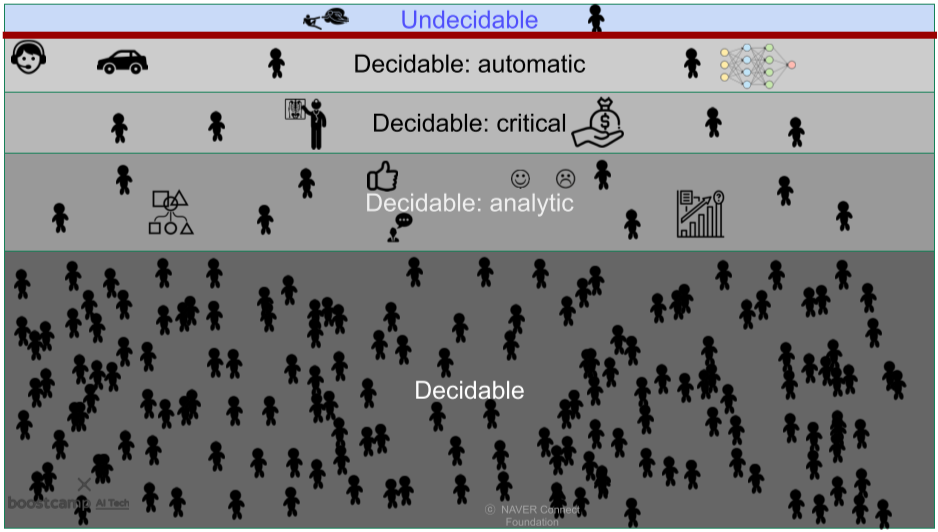
[img. 세상에는 중요한 결정과 쉬운 결정, 그리고 결정할 수 없는것이 있다]
- 근본적 가치에 관계된 일, 예측할 수 없는 일, 책임질 수 없거나 책임이 너무 큰일 등은 결정하기 힘들거나 결정할 수 없다.
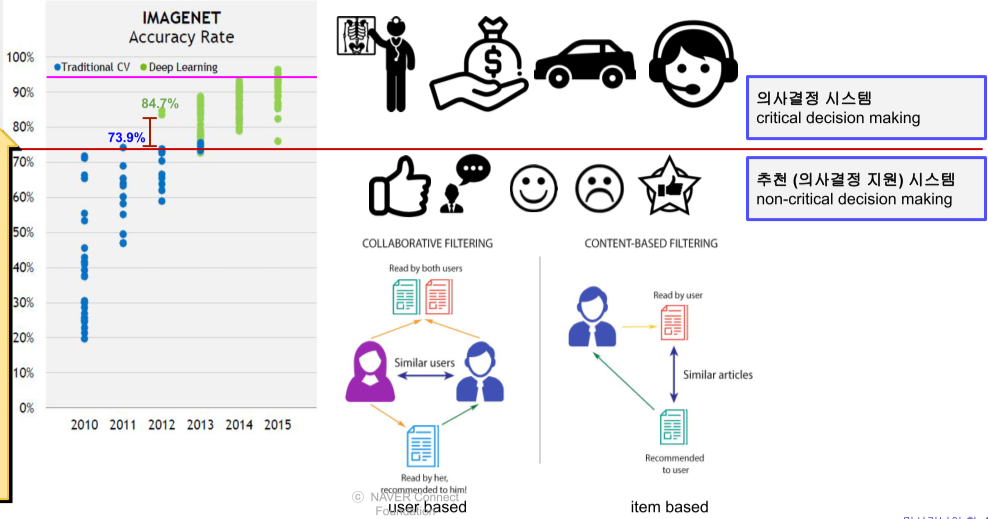
[img. 과거에는 성능 부족으로 추천 정도만 했지만 최근에는 의사결정에 관여 가능한 수준]
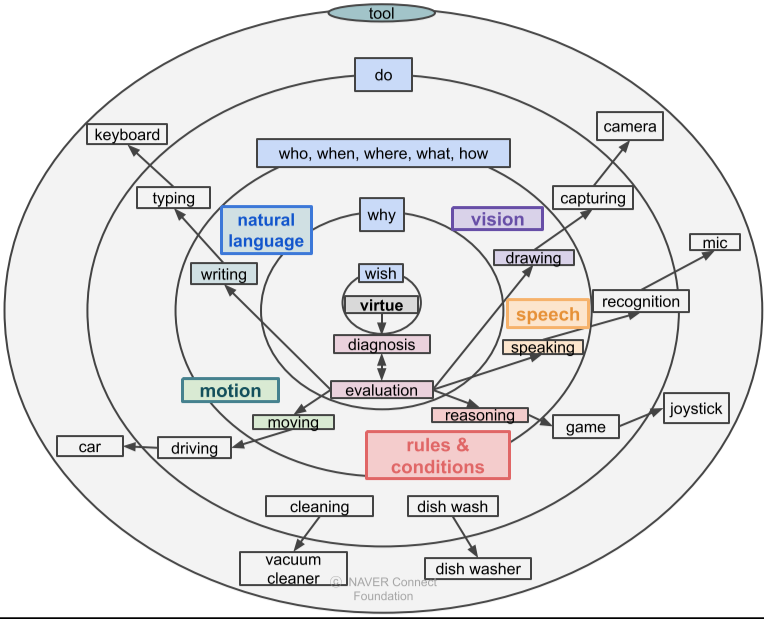
[img. 현재 기술로는 잘해봐야 Rules & conditions 까지만 결정 가능, 가치와 중요 결정은 불가]
3. 가벼운 결정기 (Lightweight decision making machine)
경량화(Lightweight)는 성능이나 가치가 차이가 없거나 적게 희생하고 규모와 비용 등을 줄이는 것이 것
소형화(Miniaturization)은 말 그대로 물건의 크기를 줄이는 것
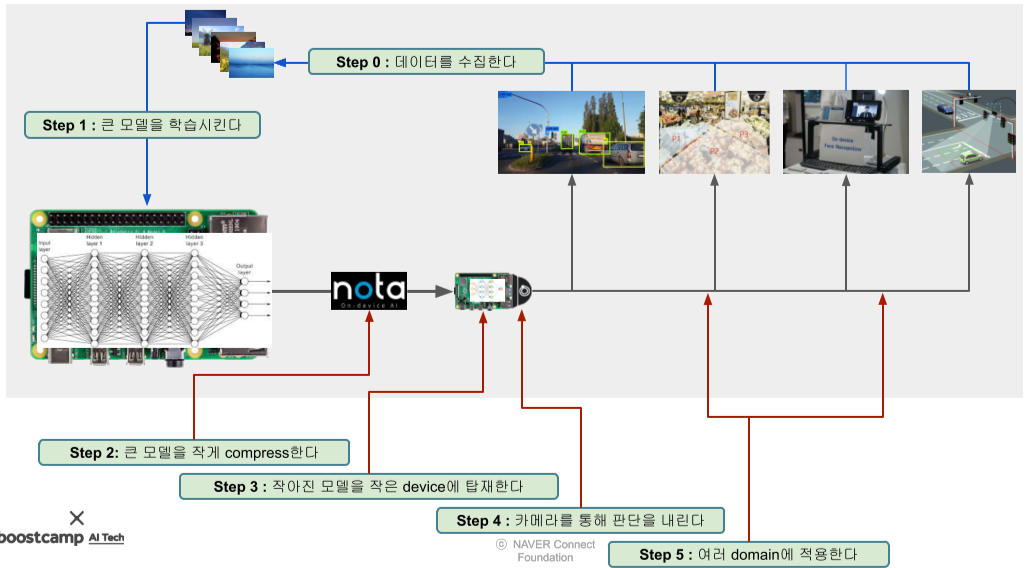
[img. 소형 기기에 ML 모델을 넣기 위한 Cycle]
최근에는 TinyML이라 하여 칩 수준의 소형기기를 위한 메모리 사용량과 연산량이 적은 Project 또한 진행되고 있다.
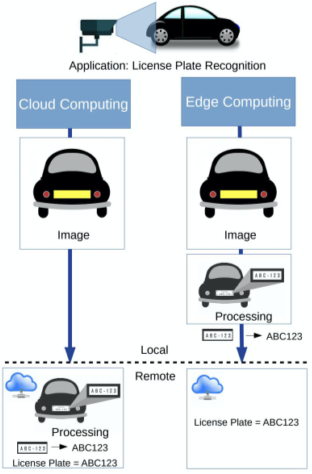
[img. Edge Computing의 장점 시나리오]
Edge Computing은 네트워크에서 끝 부분에 해당하는 보통 소형기기에서의 연산하는 서비스를 의미하며, 많은 장점을 가지고 있다
예를 들어, 자율주행의 연산을 Cloud Computing으로 처리할 시, 보안 문제, 연결안전성 문제, 대규모 연산에 의한 전력과 기기 소모 등이 필요하지만
Edge Computing은 이러한 문제를 해결할 수 있다.
4. Backbone & dataset for model compression
성능좋고 안정성 있는 Pre-trained 모델이 많이 나와있다.
이러한 Pre-trained 모델을 경량화하여 사용하면, 검증된 성능과 문제 해결, 빠른 개발 등의 장점이 있다.
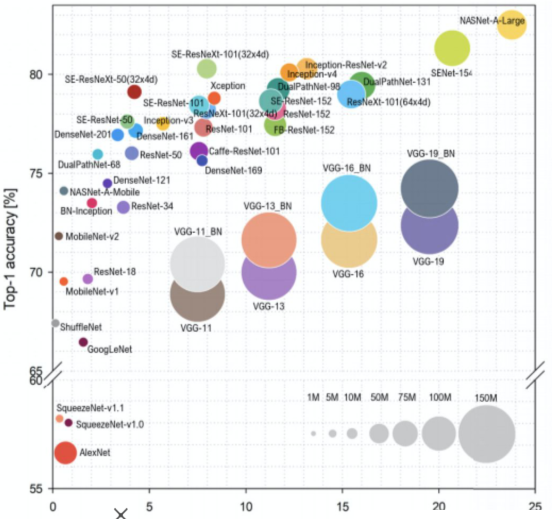
[img. 최근에는 다양한 pretrained model이 많다.]
MiB(메비바이트) : 2진법 기준 용량 계산법, 2^20 바이트
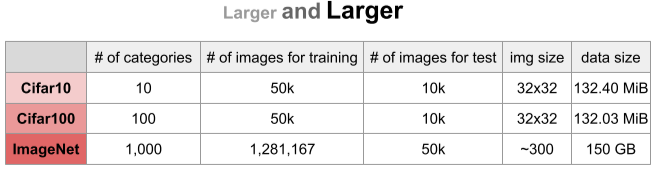
[img. Classification을 위한 Dataset들, 점점 커진다]
5. Edge devices
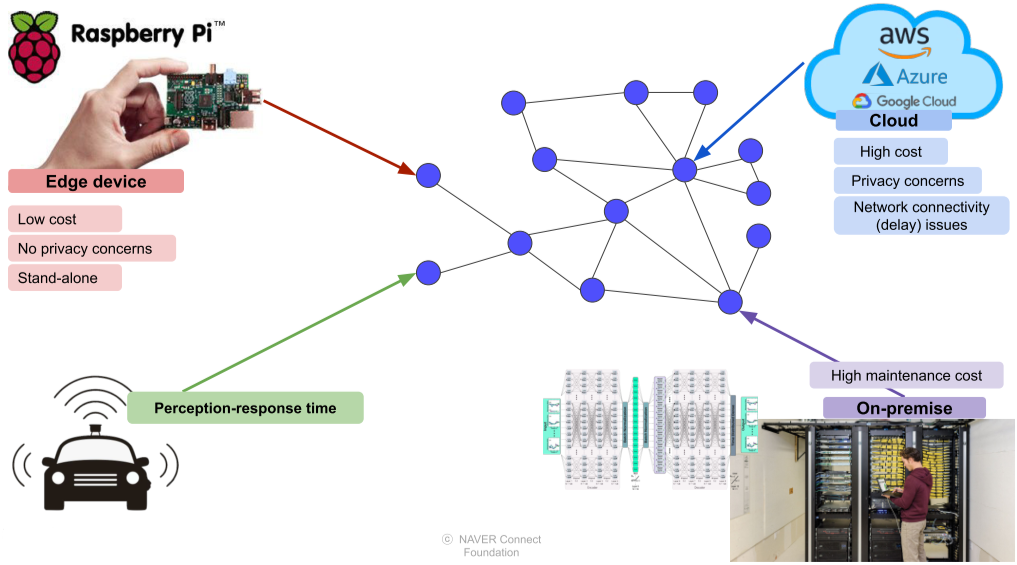
[img. 각종 computing 방법]
Cloud는 높은 가격과 보안 문제, 네트워크 연결이 필수이며, 연결이 불안전하거나 부하가 걸리면 사용하기 힘들다.
On-premise는 직접 서버를 두는 방식으로, 법적으로 정보가 네트워크에 누출 되지 않은 경우나, 대규모로 구현할 수 있는 회사등에서만 사용 가능하며, 유지보수 비용이 크다.
Edge device는 저비용, 높은 보안성, stand-alone 동작과 네트워크 연결 여부를 선택할 수 있지만, 연산량이나 전력 소모, 메모리가 제한된다는 단점이 있다.(Dumb and fast)
최근에는 Rasberry Pi, Jetson nano 처럼 합리적인 가격으로 사용해 볼 수 있다.
6. Edge intelligence
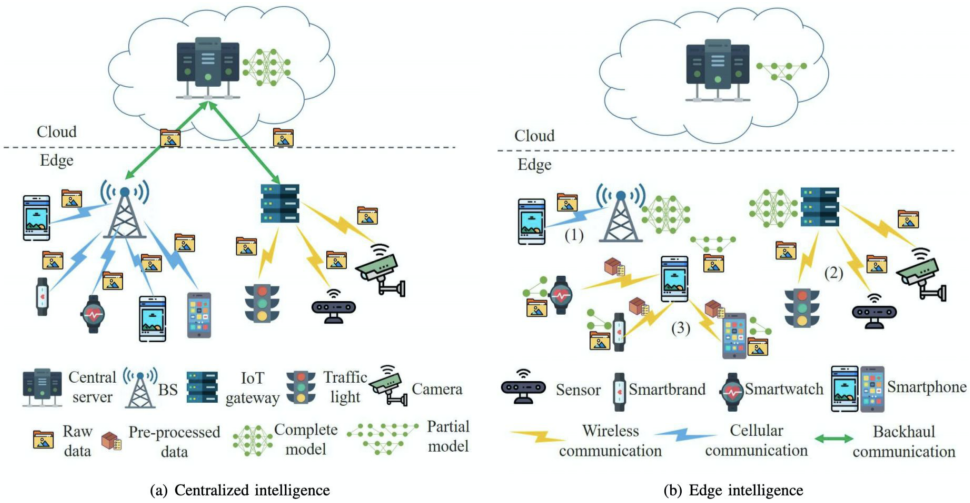
[img. Cloud intelligence vs edge intelligence]
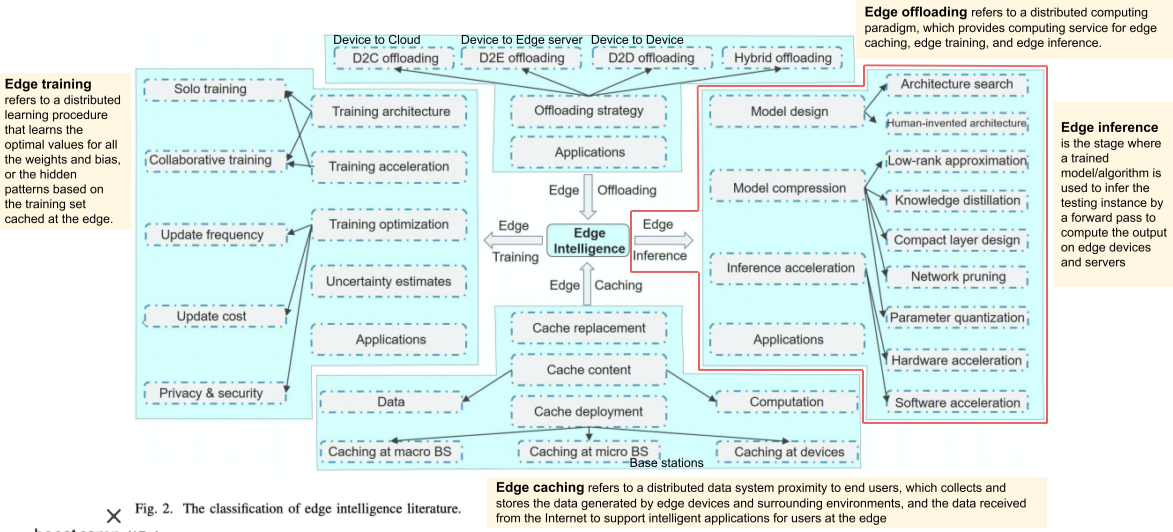
[img. edge intelligence의 내부 분류]
1) Edge training
Edge device에서 모델을 학습하는 것,
아직 Edge device 들의 성능이 떨어져 산업에서 사용하진 않는다.
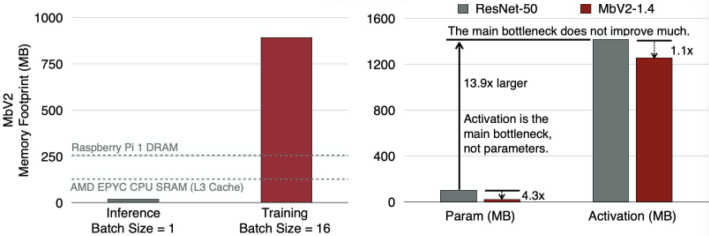
[img. Inference vs Training에 드는 비용 비교]
2) Edge caching
Edge가 처리하기 힘들지만 외부에서 연결을 통해 가져오기 힘든 정보를 연결없이 저장공간에 저장, 또는 불러오기
이번 강의에서 다루진 않음
컴퓨터 구조에서 메모리에서 hit과 miss에 대한 개념을 비슷하게 사용
3) Edge offloading
Edge와 가까운 곳에 있는 Edge 서버(클라우드와 Edge의 중간 형태)로부터 연결하여 정보를 가져옴, 하드웨어와 비슷한 개념
4) Edge Inference
수업에서 주로 다룰 분야, Edge에서 Output을 출력
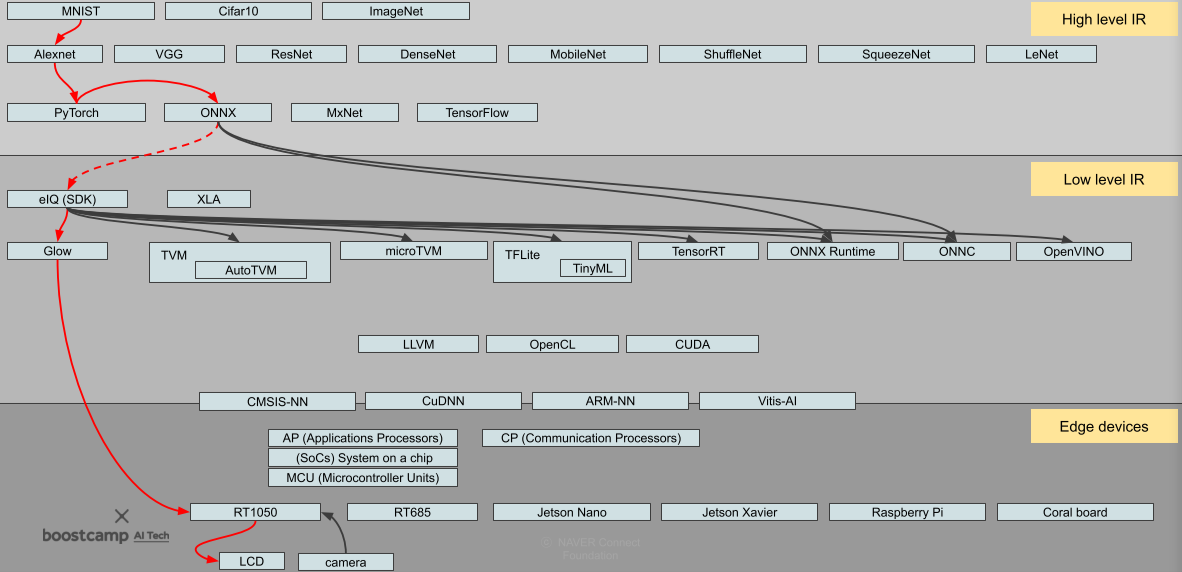
[img. model 설계의 컴파일 수준]
동전의 뒷면(The flip-side of the coin: on-device AI)
top
nvidia-smi # Gpu 상황
watch -n 0.5 nvida-smi
vmstat -h
# sudo apt-get install lm-sensors
sensors # 발열 체크
# sudo apt-get install atop
atop
# sudo apt install sysstat
mpstat
sar 3
sar 3 4
[code. system resource monitoring 방법 (Ubuntu 환경)]
AI 모델은 입력에 대해 정확한 출력을 보장하지 않음
Underspecification : 모델의 학습 결과가 매번 다름, 잘 결과를 내는 데이터가 다름
모델링 뿐만 아니라 여러가지 모두 중요하다.
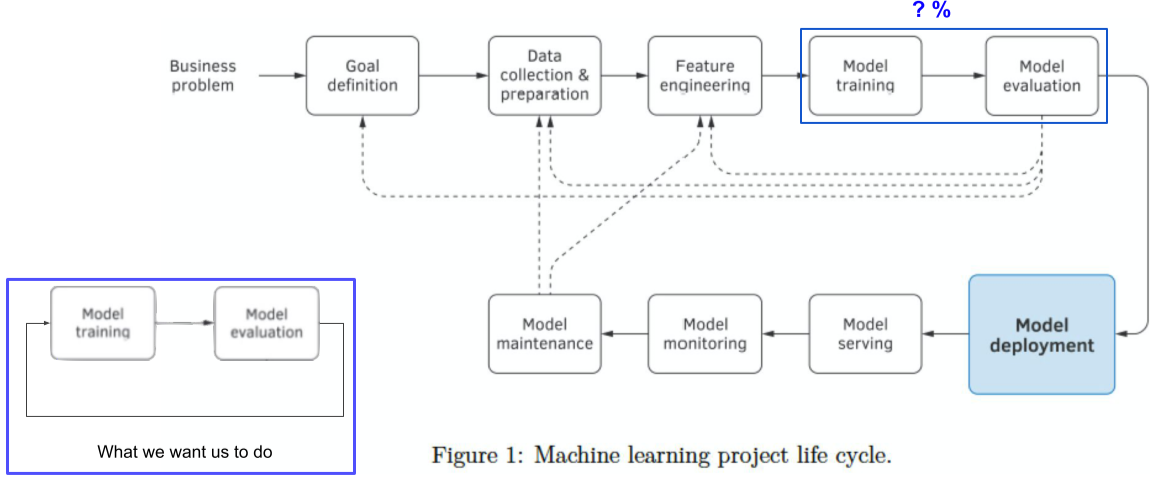
[img. 실제 ML project cycle vs 우리가 상상하던 것]
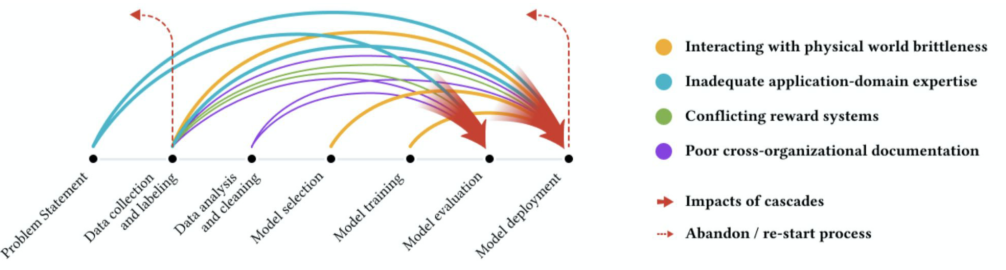
[img. 모두 모델링을 하고 싶어하고 데이터 작업은 피해요 - ML project에서의 문제는 모두 하기싫어하고 천시하는 부분에서 터진다.]
가장 적당하게 (Optimization)
제약조건 하에서의 의사결정(Decision-making under constraints)
사용가능한 자원 내에서 목적 달성 해야함
from scipy.spatial import distance
distance.euclidean([1,0,0], [0,1,0]) # euclidean 거리
distance.hamming([1, 0, 0], [0, 1, 0]) # hamming 거리
distance.cosine([1, 0, 0], [0, 1, 0]) # cosine 거리
# loss 구할 때 필요하곤 함
[code. scipy를 이용한 거리 제기]
문제란, 바라는 것과 인식하는 것 간의 차이
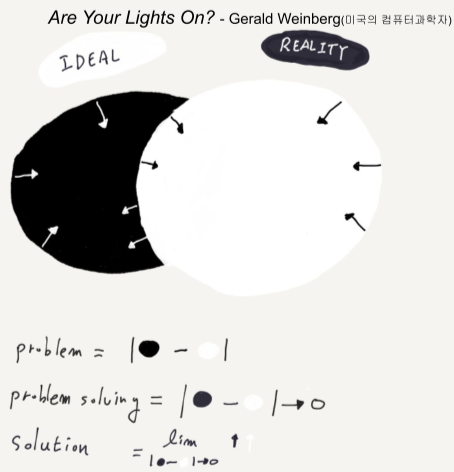
[img. 문제에 대한 그림]
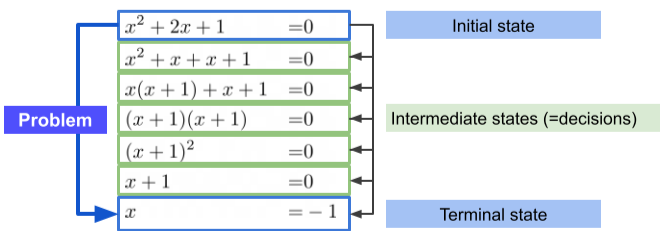
[img. 문제의 해결 과정 예시]
계산(Compute)이란, 유한한 자원과 시간 안에 decision을 통하여 Initial state부터 Terminal state까지 진행하는것 .
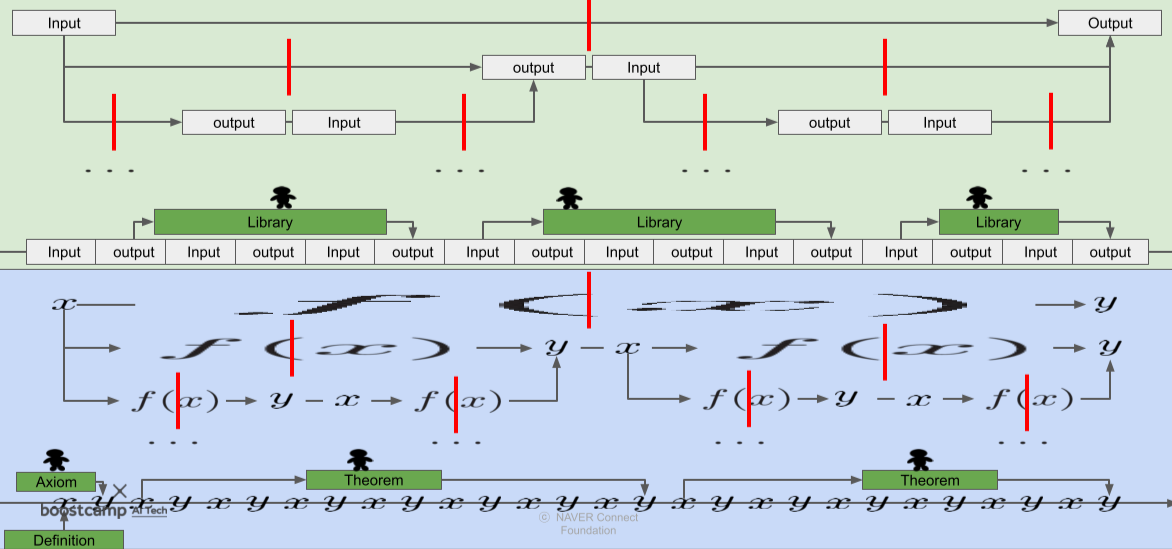
[img. 수학적 증명과 IT project의 해결과정은 비슷하다]
Decision problem : 목적만 존재 (어떻게 MST를 만드는가?)
Opitmization problem : 자원과 step에 제한이 걸린 상태에서 목적을 달성하는 법(최소 가중치의 MST를 어떻게 만드는가?)
모델의 시공간(Timespace of ML model)
search space: 답이 될 수 있는 decision, state들의 집단, state들의 합, solution space라고도 함
ex) 바둑의 기보, 알고리즘 step
problem space: 처음 문제가 정의되어 있는 공간, state, initial state라고도 함
ex) 비어있는 바둑판, 알고리즘 Input
또한, 시간을 희생해서 공간 사용량을 줄이거나 공간 사용량을 늘려 시간을 줄일 수 있는 경우가 많다.
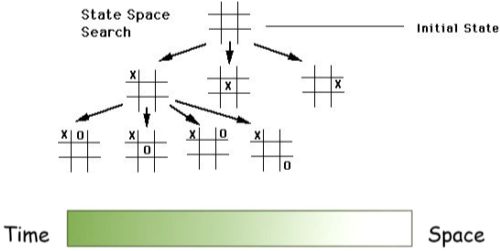
[img. Time과 space의 trade off]
Time Complexity : Input size에 따라 얼마나 Problem solving Time이 늘어나는가?
기존의 알고리즘은 P 문제까지 손쉽게 해결 가능하다.
NP 문제부터는 머신러닝으로 해결할 수 있다.
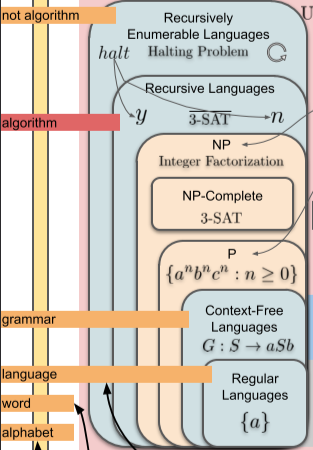
[img. 시간 복잡도에 따른 문제 분류]
entropy : 무질서도 그리고 정보, 놀라움, 불확실성의 레벨
문제 해결은 높은 entropy의 상태를 에너지를 투자하여 낮은 entropy로 바꾸는 것,
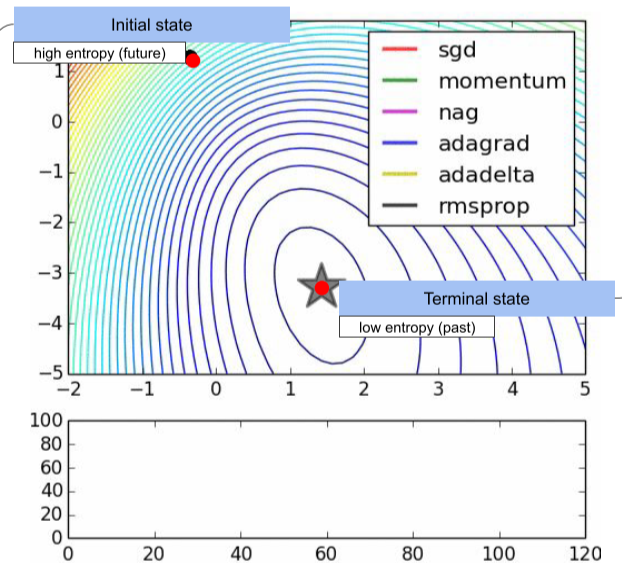
[img. ML에서 Loss값을 줄이는 행위 또한 entropy를 낮추는 것이다.]
parameter search
과거의 도구는 인간이 직접 설계하고, 제작하여, 사용하여야 했다.
공학과 에너지의 발전으로 인간이 직접 설계하고 제작하면, 자동으로 사용되는 기계가 생겨났다
이후 프로그래밍의 발전으로 인간이 프로그램을 설계하면 프로그램의 제작과 사용이 자동화되는 시대가 되었다
머신러닝을 통하여 Parameter Search를 통하여 프로그램의 로직을 자동으로 설계할 수 있게 되었고,
앞으로 딥러닝과 먼 미래에는 Hyperparameter와 Architecture 또한 자동으로 설계가 되어, 완벽한 자동화가 이루어질 것이다.
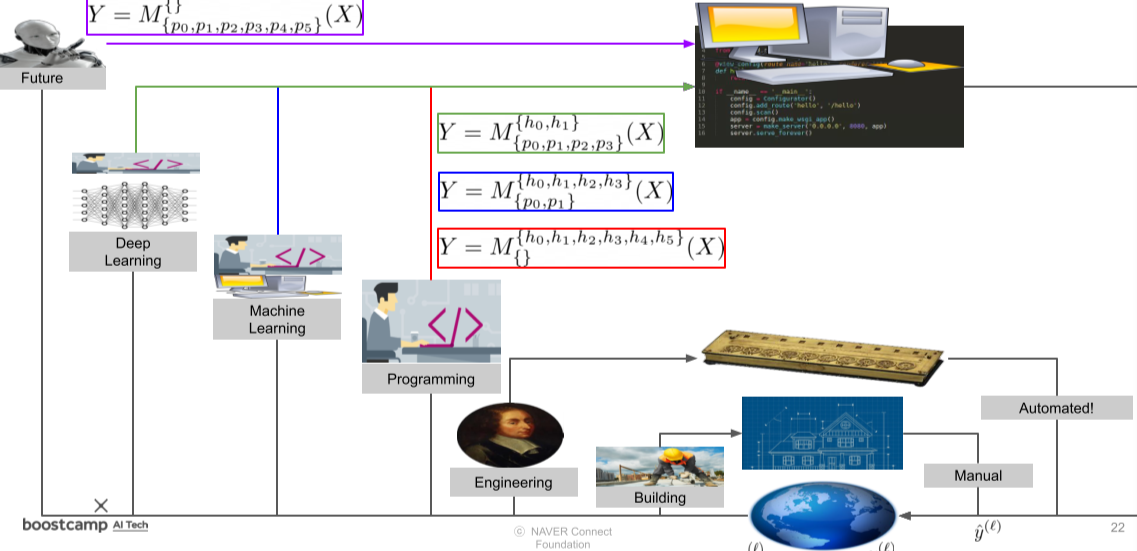
[img. 도구의 역사]
딥러닝에서 데이터는 벡터나 다차원 array 등으로 다양하게 표현할 수 있다.
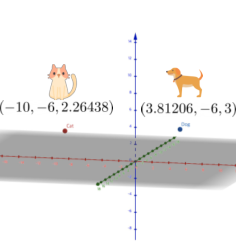
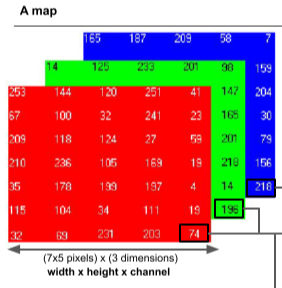
[img. Data의 Vector 표현과 map 표현]
Classification task의 경우 위에서 표현한 데이터들의 차원상의 Decision boundary를 결정하기 위해, layer를 통하여 차원에서의 표현을 바꾸는 과정을 거친다.
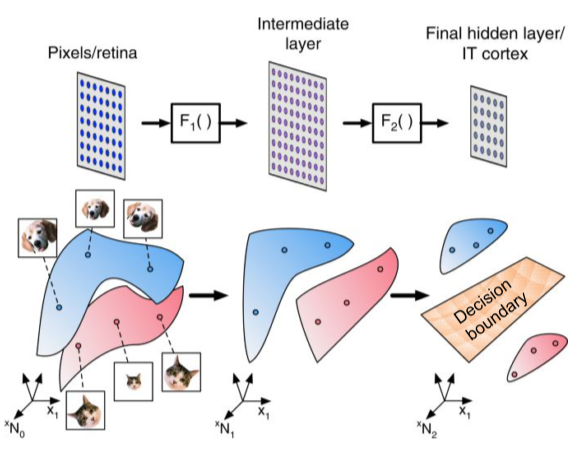
[img. Decision boundary를 결정하기 위한 geomerty 변경]
Hyperparameter search
Hyperparameter search의 경우 parameter search와 다르게 하나의 weight가 아닌 전체적인 구조에 영향을 주는 경우가 많아 parameter search 보다 더욱 리스크와 cost가 크다. (ex) 레이어의 수, learning rate 등)
이를 해결하기 위해 다양한 연구가 진행되고 있다.
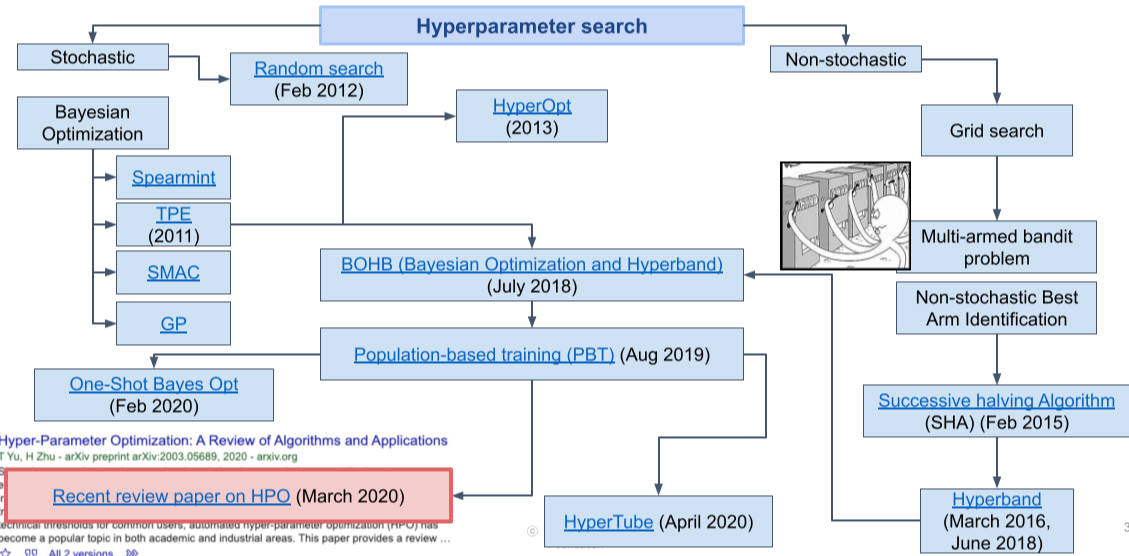
[img. Hyperparameter seach에 대한 연구]
Hyperparameter 탐색 시마다 간격을 일정하게 주는 Grid search와 random한 값을 주는 Random search가 있으며, 기존의 Manual search와 비교해서 다음과 같은 장단이 있다.
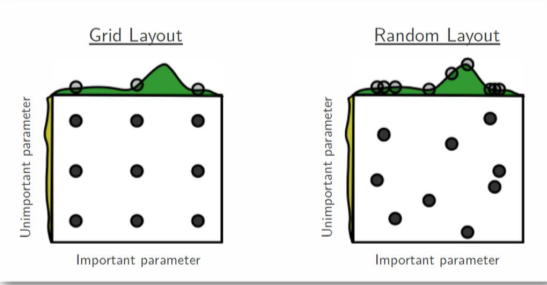
[img. hyper parameter search 방법]
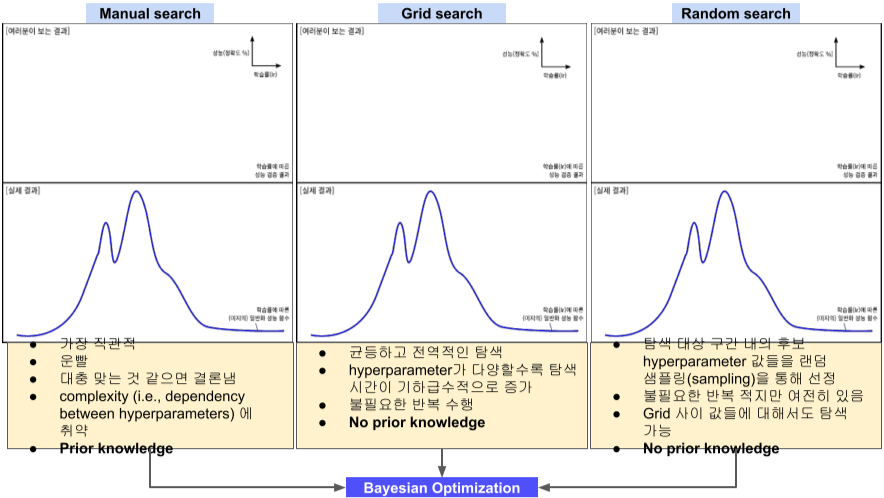
[img. search 방법에 따른 성능 차이]
또한 단순한 Random search 말고도, Hyperparameter에 따른 결과를 예측하는 모델을 만드는 방법인 Surrogate model이라는 방법이 있다.
- Gaussain Process가 대표적인 방법
- 조금더 적은 비용으로 많은 탐색이 가능하다.
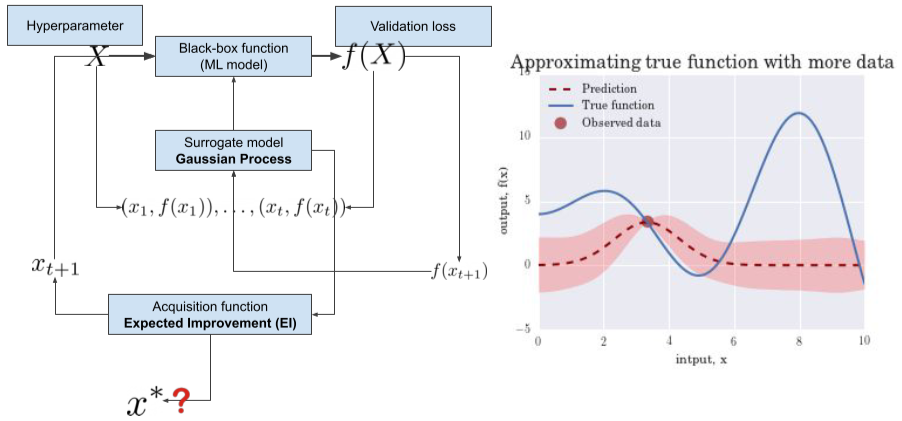
[img. Surrogate model 도식]
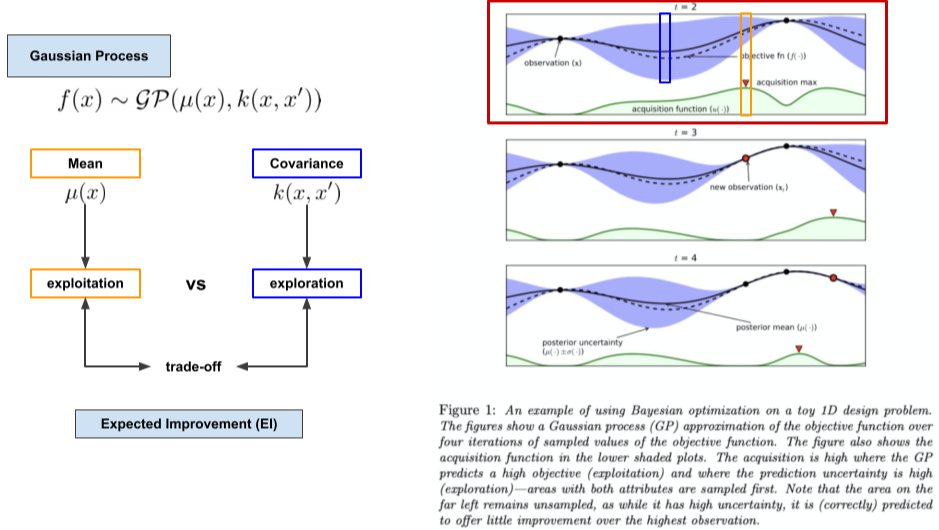
[img. Gaussian model 예시]
Neural Architecture search(NAS)
NAS는 보통 사람이 직접 만든는 것도 포함하는 개념이지만 좁은 의미에서는 마치 parameter를 찾는 것 처럼, 효율적인 ML구조를 Neural Archtecture 또한 탐색을 통하여 찾는 방법이다.
Multi-objective NAS의 경우, 성능 뿐만 아니라 최적화도 신경쓰므로, Optimization에도 뛰어나다.
결과물은 사람이 이해할 수 없지만 괴상한 구조인 경우가 많다.
이 때, 단순히 완전 탐색을 통하여 Search 하는 것이 아니라, NAS 전략을 위한 머신러닝 모델을 만들 수도 있다.
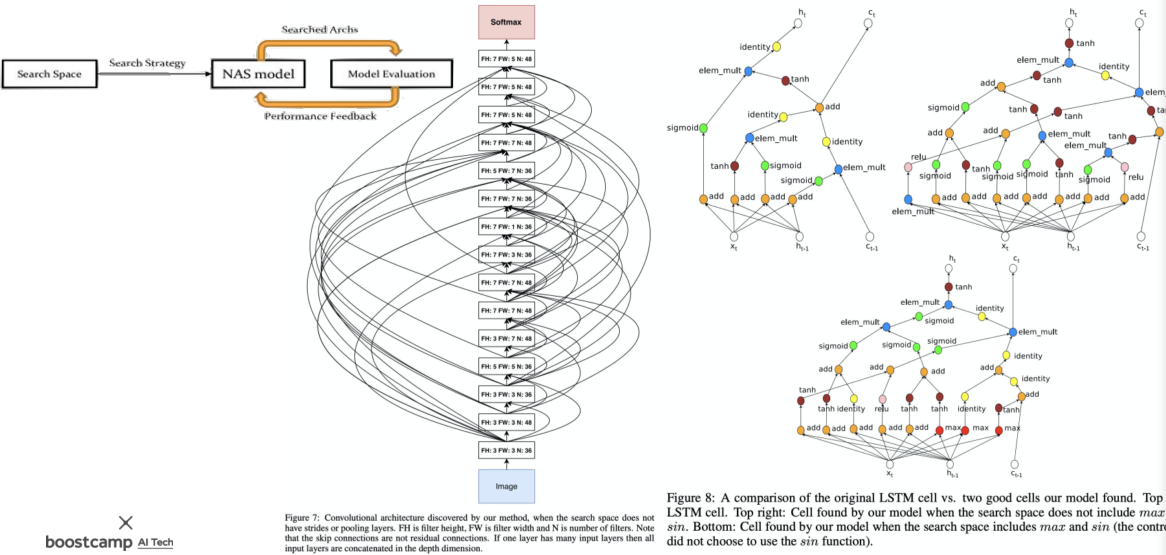
[img. Automatic Neural Architecture Search]
NAS for edge device
- MnasNet
edge device를 위한 NAS
model들을 샘플로, 실제 Mobile phone환경에서 실험한 결과를 reward로 하는 강화학습을 통하여 기존의 모델 보다 성능과 latency 를 개선함.
Hyperparameter search를 하듯 Block 별로 layer의 종류와 parameter를 지정하고 search함.
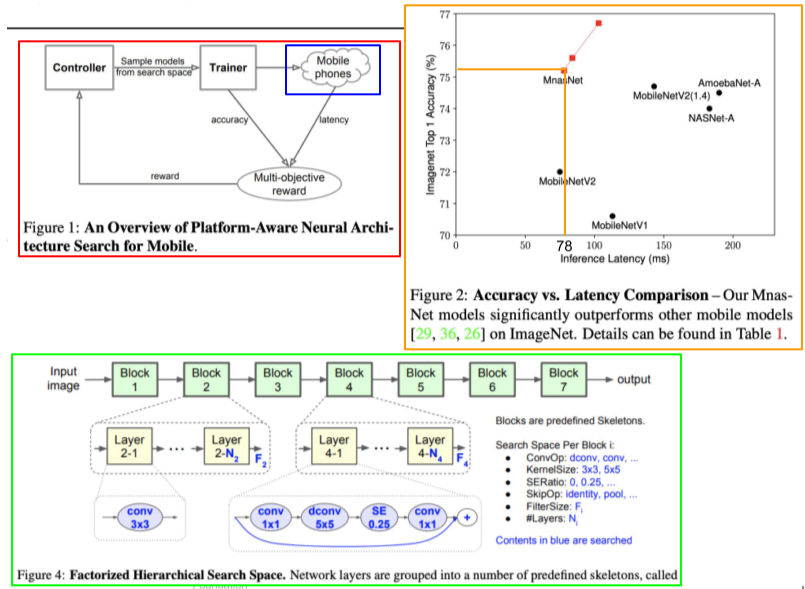
[img. MnasNet 논문 내부의 figure]
- PROXYLESSNAS
과거에는 Proxy를 이용해 NAS를 하였지만 이 방법의 결과가 실제 결과와 괴리가 있는 경우가 많으므로 ,PROXY를 사용하지 않은 NAS 방법
- Proxy는 직접적으로 실제 모델을 학습하면서 NAS를 돌리면 너무나도 비용이 크므로 일종의 간략화된 가짜 모델을 이용해 학습하는 방법

[img. PROXYLESSNAS의 figure]
- ONCE-FOR-ALL
Training한 모델을 단순히 한 Device 뿐만 아니라 조금의 구조 변경을 통해 여러 Platform에 적용
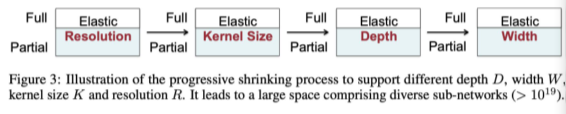
[img. ONCE-FOR-ALL의 비결, Pruning 방법과 비슷함]
- MobileNet 시리즈
CV 시간에 배운 Depth-wise Separable Convolution에 대한 내용
나중에 또 나온다고함
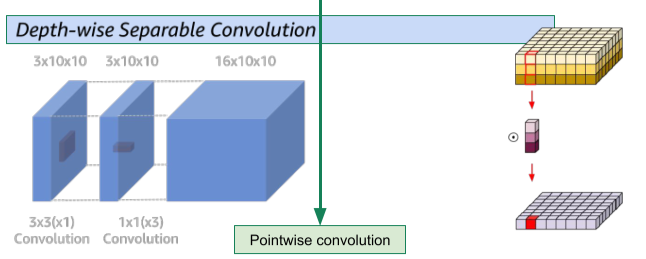
[img. Depth-wise Separable Convolution]
압축
압축 (Compression)
\[Compression\ rate =\frac{size\ before\ compression}{size\ after\ compression}\][math. 압축율(Compression rate)의 정의]
- 손실 압축
데이터를 눈치채지 못하는 수준의 손실시켜 압축
압축률이 상당한 경우가 많으며, 손상되도 문제 없는 경우에 사용됨
- 예를 들어, 화질, 음질의 저하는 눈치 못채는 경우가 많다.
- jpg, mp3, mp4, avi, gif 등이 있다.
- MP3는 일반 WAV보다 약 12% 이하의 크기
- 가청주파수 이외의 음은 잘라내버리는 방식
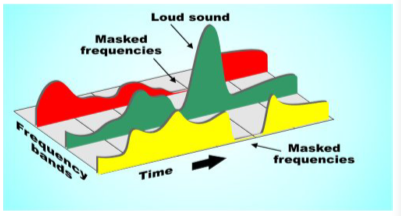
[img. audio data의 손실 압축]
- 비손실 압축
복원 시, 데이터가 손실되지 않은채로 완벽하게 복원됨
압축률은 데이터마다 다르겠지만, 보통 손실 압축보다 덜압축됨
- 비손실 압축의 예시로 Run-length encoding (RLE)가 있다
[img. RLE의 압축 방법]
- zip, 7-zip, wav, flac, png 등이 있다.
Huffman coding
압축 알고리즘 중 하나
문자에 대한 코드 map을 생성하여 문자대신 해당 코드로 압축, 이때 많이 등장한 단어에는 짧은 코드를, 적게 등장한 단어에는 긴 코드를 할당하여 압축률을 극대화
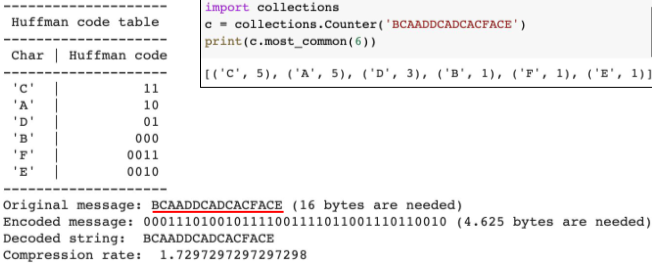
[img. Huffman coding 중 하나]
부호 (Coding)
압축은 특정 정보를 인코딩(enCODING)하고 또, 그것을 디코딩(deCODING)하여 원본 크기로 바꿀 수 있을 때, 압축 크기가 원본크기가 작으면 압축이라고 정의한다.
즉 압축은 Coding의 일부
Finite State Machine(FSM)
상태를 의미하는 정점과 상호작용을 의미하는 간선들로 객체의 상태와 변화, 동작을 표현하는 방법
각 정점 또한 초기 상태, 중간 상태, 종료 상태로 나뉜다.
컴퓨터 그 자체와, 그와 관련된 개념들이 이를 이용한다.
ex) Client-Sever 관계(Client의 Request와 Server의 Response)
DB의 데이터에 대한 CRUD 로직
알고리즘 문제의 Input state, Step, Output state
등이 존재함
부호화(EnCoding)한다는 공통점이 존재
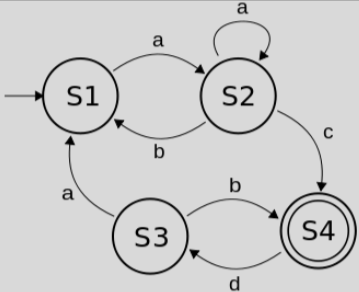
[img. FSM의 그림]
머신러닝 또한 Input data를 encoding 해서 output을 만드는 Coding 이다.
[img. 머신러닝 모델 생성의 FSM 표현]
부호화 (Encoding)
KL divergence는 Loss를 많이 구하는데 사용하지만, 엄밀히 말하면 entropy의 차이를 측정할 수 있는 방법이며, 압축 등의 효율을 구하는 데도 사용한다.
P분포와 Q분포의 차이를 찾음
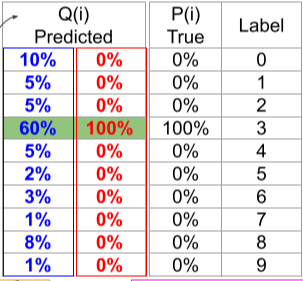
[img. Mnist Model의 예측 결과]
\(D_{KL}(P\|Q)=\mathbb{KL}(P\|Q) = -\mathbb{E}_{x\sim P(x)}[logQ(x)] + \mathbb{E}_{x\sim P(x)}[logP(x)]\\
=-\sum^9_{i=0}P(i)\ln\frac{Q(i)}{P(i)}=\sum^9_{i=0}[(-P(i)\ln Q(i))-(-P(i)\ln P(i))]
\\ 크로스\ 엔트로피: -\mathbb{E}_{x\sim P(x)}[logQ(x)], 엔트로피:\mathbb{E}_{x\sim P(x)}[logP(x)]\\\\
파란\ 예측 : D_{KL}(P\|Q)=0.5108\\
빨간\ 예측: D_{KL}(P\|Q)=0\)
[img. KL divergence를 통한 Loss값 측정 및 결과]
머신러닝이 Loss값을 줄이는 행위 또한 Encoding이라고 함
압축에서의 Cross-entropy의 의미는 q의 분포 코드 북으로 p 코드북을 사용하는 문장을 해석 했을 때의 평균 길이
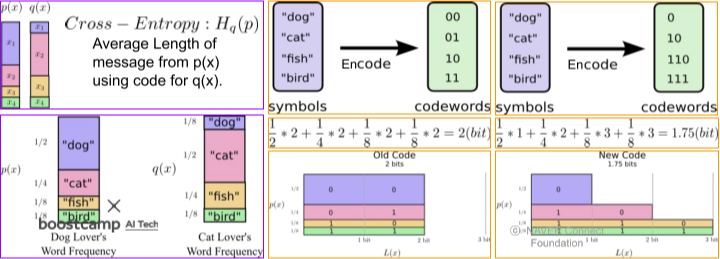
[img. 압축에서의 Cross-Entropy의 의미]
압축률(Compression rate)
머신러닝의 압축에서 다음과 같이 정의할 때
| Original Model | Compressed model | |
|---|---|---|
| Models | $M$ | $M^*$ |
| The number of the parameters | $a$ | $a^*$ |
| The running time | $\mathcal{s}$ | $\mathcal{s}^*$ |
[img. 압축된 모델의 정의]
각 성능을 의미하는 지표를 구하는 방법은 다음과 같다.
\(Compression\ rate: \alpha(M,M^*)=\frac{a}{a^*}\\
Space\ saving\ rate: \beta(M,M^*)=\frac{a-a^*}{a^*}\\
Speedup\ rate: \delta(M,M^*)=\frac{\mathcal{s}}{s^*}\)
[img. 성능 비교용 지표 ]
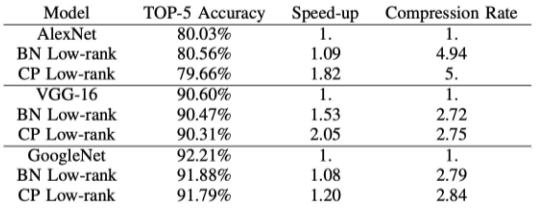
[img. 각 모델 성능의 비교 ]
DEEP Compression 논문에서 Pruning, Quantization, Huffman coding을 이용한 모델 압축 후의 성능과 압축율에 대한 정보가 나와있다.
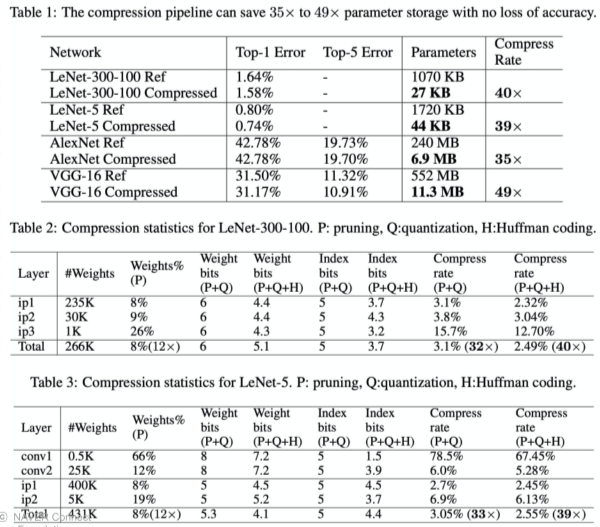
[img. 기존 모델의 압축과 압축에 따른 성능 비교]
압축이 크게 된 Layer는 쓸모없는 Parameter가 많았다는 의미이다.
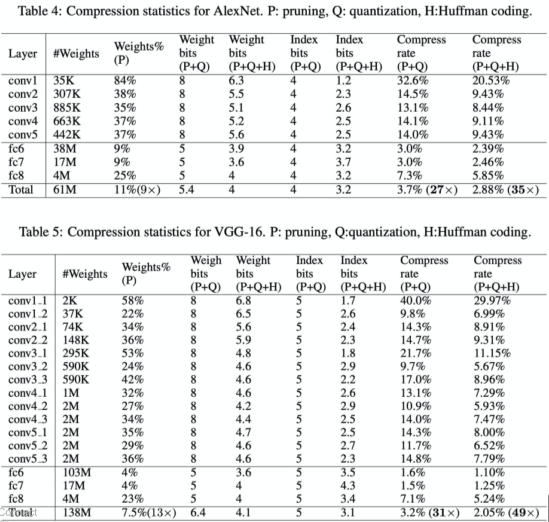
[img. AlexNet의 Layer 별 압축 결과]
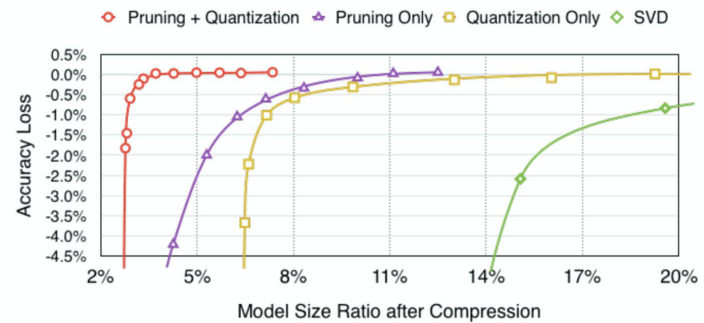
[img. Compression 비율에 따른 정확도 그래프]
TFlite를 사용하면 크게 압축 된다.
Acceleration
우리가 배운 pytorch는 framework 수준이며 실제 구동에서는 더욱 더 낮고 Low level로 compile 되게 된다.
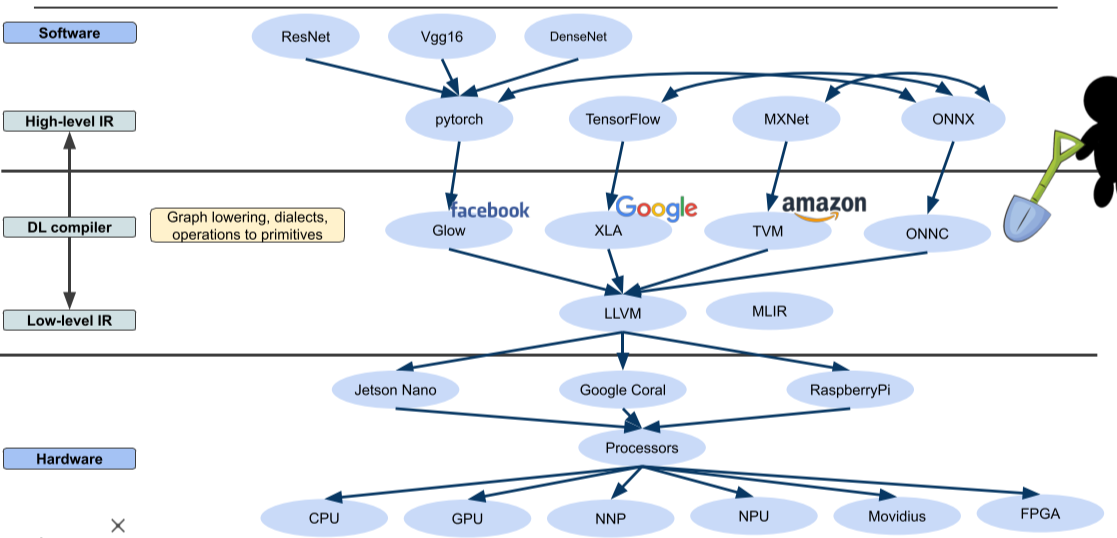
[img. DL Software~Hardware 까지]
Acceleration
Numpy는 C 기반이라 병렬적으로 처리가 가능, 메모리에 효율적으로 배치되어서 Python List보다 훨씬 빠름
Python은 Intepreter 언어
C는 Compile 언어
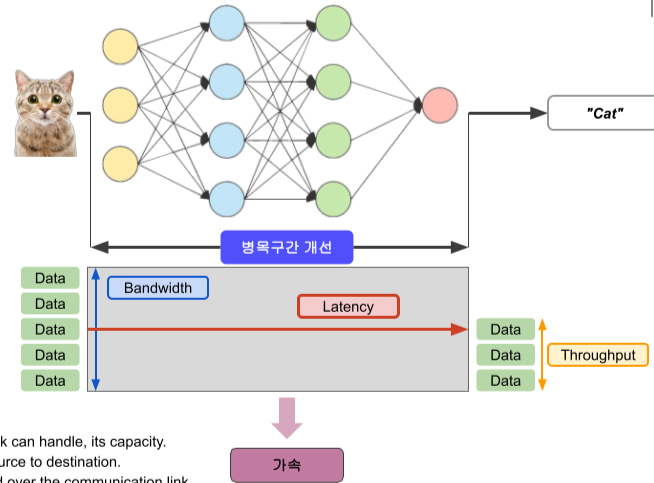
[img. Bandwidth와 Throughput에 대한 개념]
[img. Latency에 대한 개념]
Bandwidth는 시간당 얼마나 CPU가 데이터를 주고 받을 수 있는가에 대한 능력
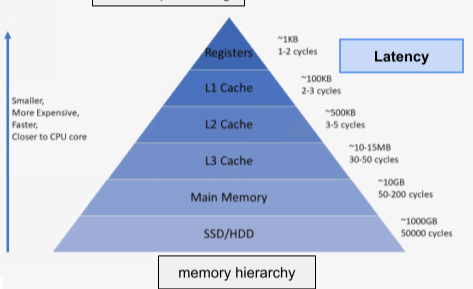
Latency는 정보가 전송될 때 지연되는 시간(메모리간의 속도 차이, 데이터의 병목, 너무 많은 명령 처리 등으로 인해)
Throughput은 실제 데이터가 전송되는 양
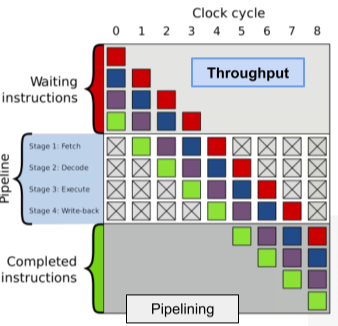
Parallel processing은 Throughput이 좋아지며, latency와 badnwidth는 변화없다.
[img. ML에서의 가속 방법]
이때, 모델의 속도를 개선하기 위해, Multithreding 디자인 또는 Low-Precision arth metic, data flow 개선, in-memory computing capabilty 증가 등의 방법이 있다.
Hardwares (chip)
하드웨어 가속(Acceleration)을 통하여 latency를 줄이고, throughput을 늘리는 효과를 가질 수 있다.
- 이때, 하드웨어 가속(Acceleration)은 잘 수행할 수 있는 특정 목적에 맞게 하드웨어를 이용하거나 설계하는 것이다.
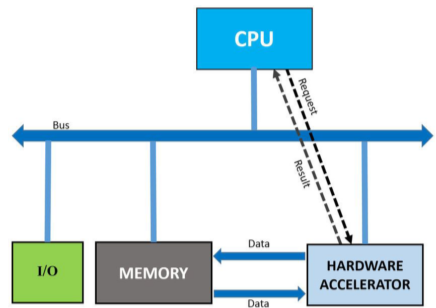
[img. about hardware acceleration]
Processing Unit은 많은 종류가 있다, ARM이 대세
| 명칭 | 의미 | 설명 |
|---|---|---|
| CPU | Central Processing Unit | 범용 |
| GPU | Graphic ProcessingUnit | 이미지, 컴퓨터 그래픽, 게임 |
| DPU | Data ProcessingUnit | 데이터 |
| TPU | Tenor ProcessingUnit | 2차원 이상의 array, NPU에 속함 |
| NPU | Neural ProcessingUnit | 딥러닝 |
| IPU | Inelligence ProcessingUnit | 그래프코어에서 생산 |
| VPU | Vision ProcessingUnit | |
| FPGA | Field Programmable Gate Array | 조립 가능, 아두이노 같은 것 |
| SoC | System on Chip | CPU,GPU,Memory,Camera등 모든 기능을 탑재 |
| ASIC | Applicatioin Specific Integrated Circuits | 특정 목정만을 위한 칩(냉장고, 밥솥 등) |
| Neuromorphic IC | Neuromorphic Integrated Circuit |
[img. Processing uint 차이]
IPU는 메모리와 코어와의 거리가 짧아 병목현상과 Latency가 적다.
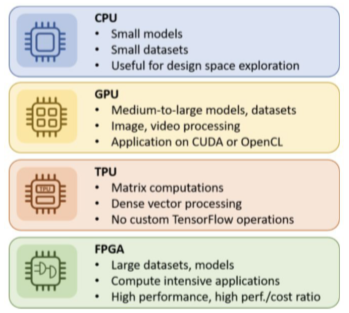
[img. 가장 많이 사용되는 4개의 Processing uint]
CPU는 범용 목적이며, 순차적인 업무에 전반적으로 성능이 좋음
GPU는 병렬 처리에 유리하며 그래픽 업무, 병렬 처리가 필요한 ML에 좋음
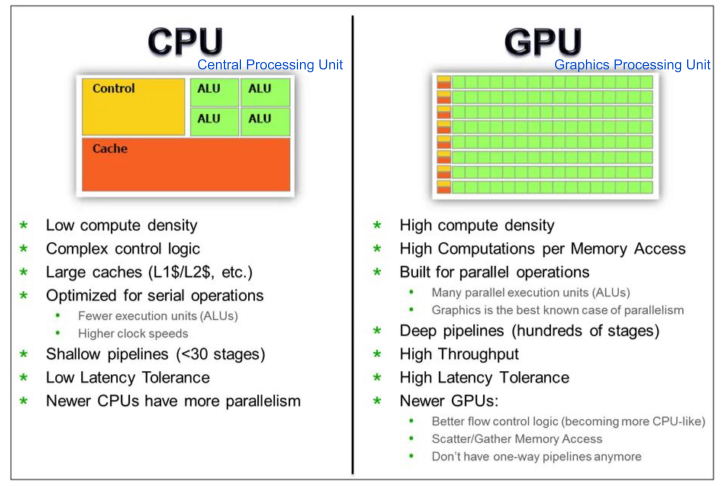
[img. CPU vs GPU]
Compression & Acceleration
Compression : 보통 소프트웨어 단에서 용량을 줄이는 등에 사용 (Space complexity로 계산)
Acceleration : 보통 로우레벨 또는 하드웨어 단에서 연산속도, Latency 등을 개선하는데 사용 (Time complexity로 계산)
칼같이 구분하진 않음
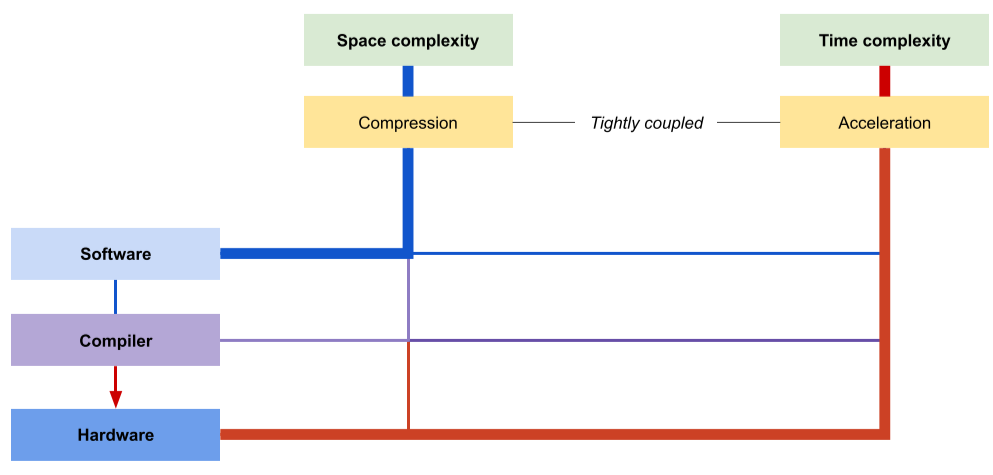
[img. Compression과 Acceleration의 차이]
하드웨어를 고려한 Compression이 더욱 효과적임
하드웨어 + 소프트웨어 co-design
Deep learning compiler
DL compiler는 다른 framework에서 만들어진 DL model을 Input으로 받아서 여러 hardware에 최적화된 DL code를 출력하는 compiler다.
- XLA, TVM, GLOW, ONNC 등이 존재함
multi-level IRs : 여러 단계를 걸쳐 시행
frontend/backend optimization : High level <-> lowlevel 구조
- frontend/high level은 하드웨어에 Independent 하다
- backend/low level은 하드웨어에 따라 다르다.
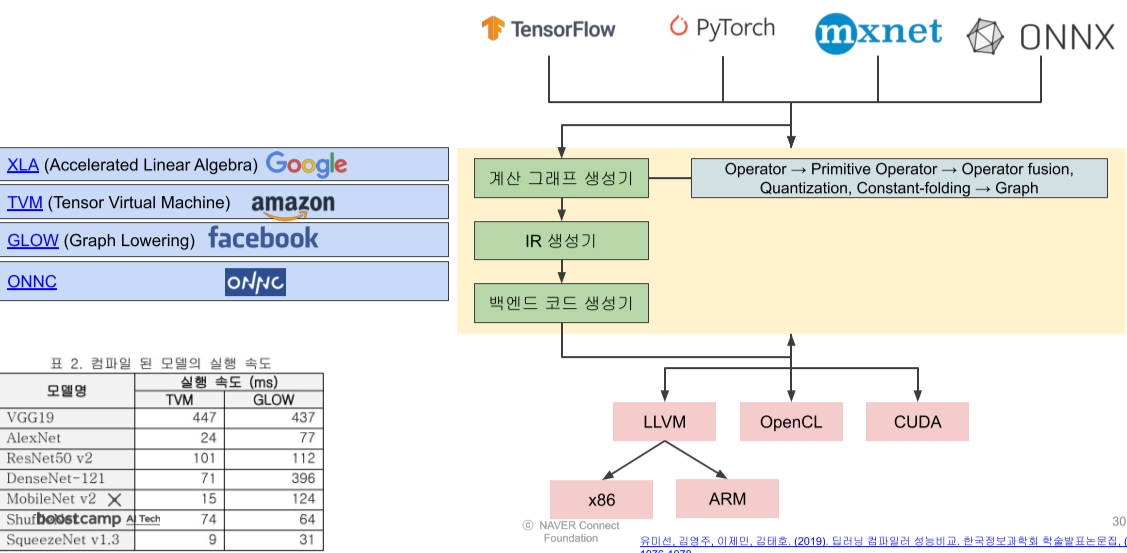
[img. High level과 low level의 예시]
LLVM
LLVM IR을 사용하여 언어 <-> 하드웨어 간의 번역을 통합함
컴파일러 수가 크게 줄어듦
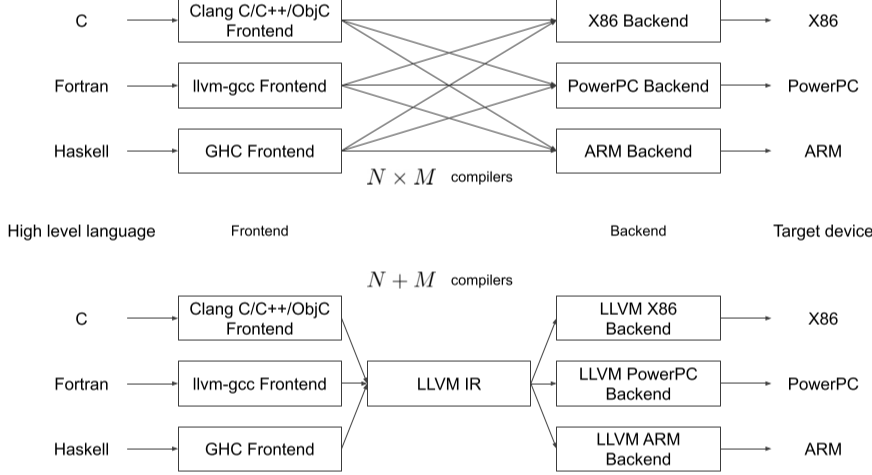
[img. LLVM의 장점]
MLIR(Multi-Level Intermediate Representation)
머신러닝 컴파일러 생성을 도와주는 library
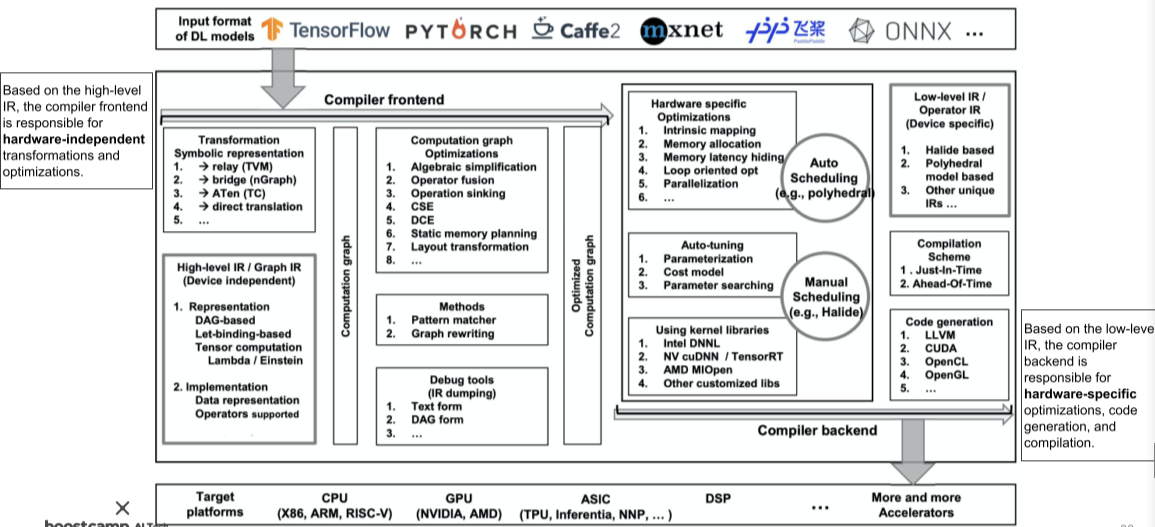
[img. 자세한 ML 모델의 컴파일 과정]
compiler backend optimization 예시
polytotype method : loop 문에 관한 optimization 방법
Locality of reference : 사용했던 데이터는 또 다시 쓸 확률이 높으므로, 메모리 위치를 조정해줌
- Temporal locality
- spatial locality
- Branch locality
- Equidistant locality
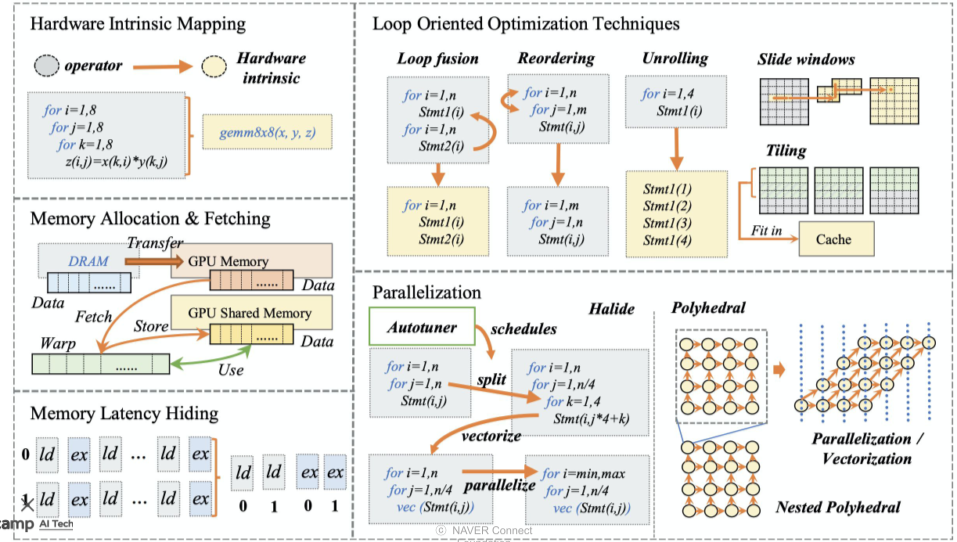
[img. Hardware단의 compile의 여러 예시]
Structured pruning + Mixed precision quantization = Harware-ware compression
단순히 소프트웨어 만으로 최적화하지 않고 hardware에 맞추어 최적화하는 것,
[img. Hardware-aware compression ]

[img. compression의 최신 트랜드]
가지치기(Pruning)
Weighted sum model
\[S = \sum^N_iw_ix_i=(w_1,w_2,\dots,w_N)\cdot(x_1,x_2,\dots,x_N)=W\cdot X, (W,X) \in \mathbb{R}^{N\times N}\][math. weighted sum 공식]
Pruning이란?
중요한 node만 남기는 방식으로 optimization
장점으로 추론 속도증가, 모델의 complexity 감소, Regularization으로 인한 generalization 성능 향상
단점으로 정보의 손실압축 형식, 하드웨어 기반 optimization이 까다로워짐, acc loss
그다지 중요하지 않은 정보는 weight가 0에 가깝게 생성되므로, 큰영향을 끼치지 않는다.
weight가 0에 가까운 neuron을 pruning하여 opimization할 수 있다.
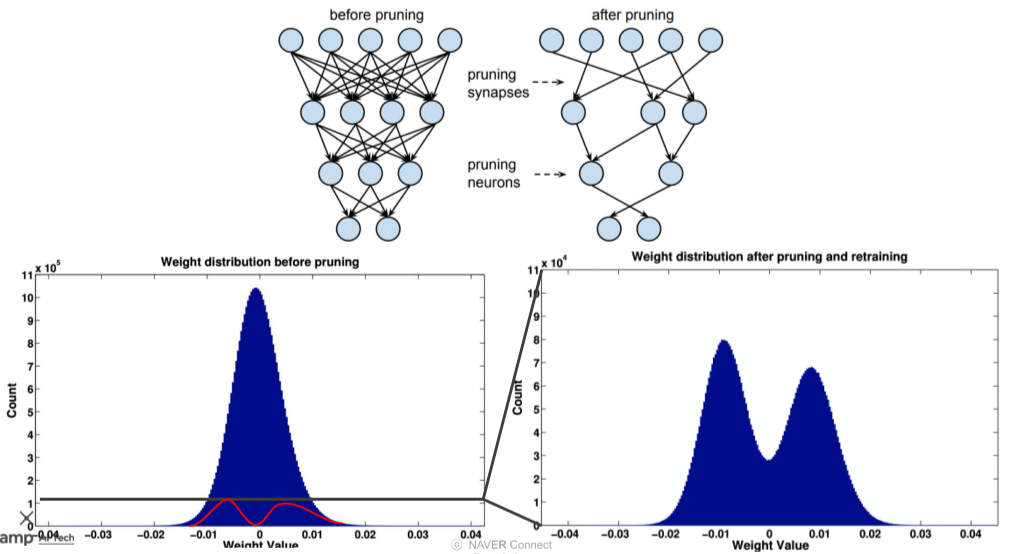
[img. Pruning의 결과]
Dropout 또한 Regularization을 위해 사용하며, 랜덤으로 Drop하게 되면 다른 모델처럼 되므로 앙상블과 비슷한 효과를 가질 수 있다.
Dropout과 Pruning의 차이는 Dropout은 매번 training마다 랜덤하게 끄고, Inference 시 다시 켜지지만, Pruning은 아니다.
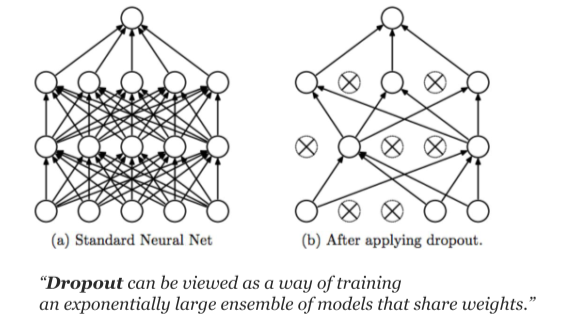
[img. Dropout]
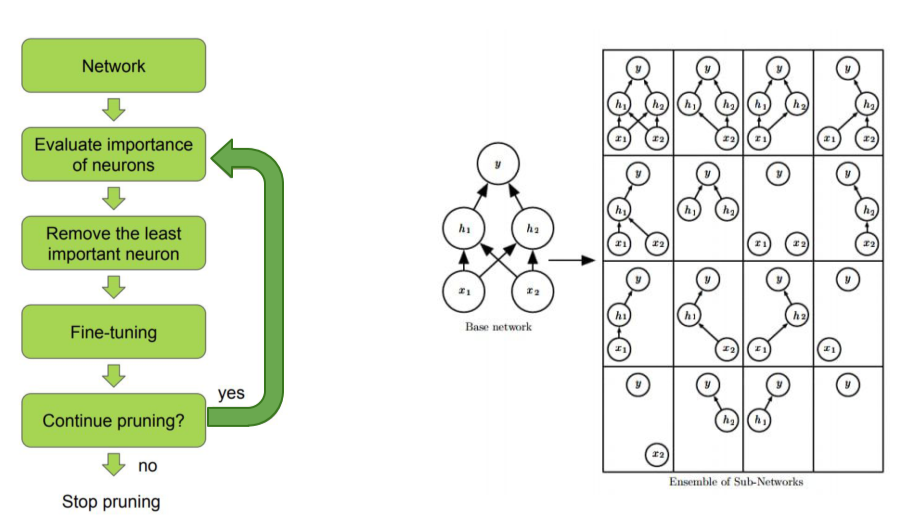
[img. Pruning(좌), Dropout(우)]
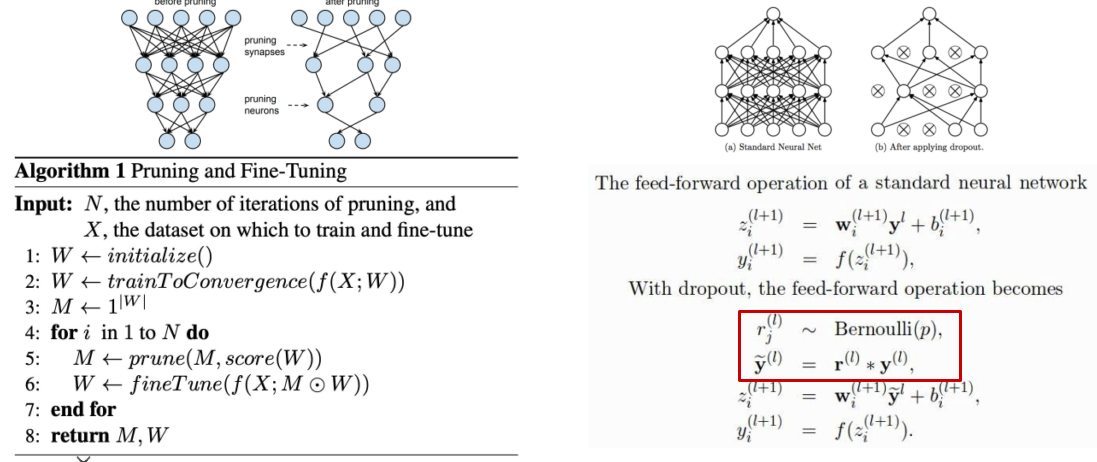
[img. Prunnig과 Dropout의 수식적 차이]
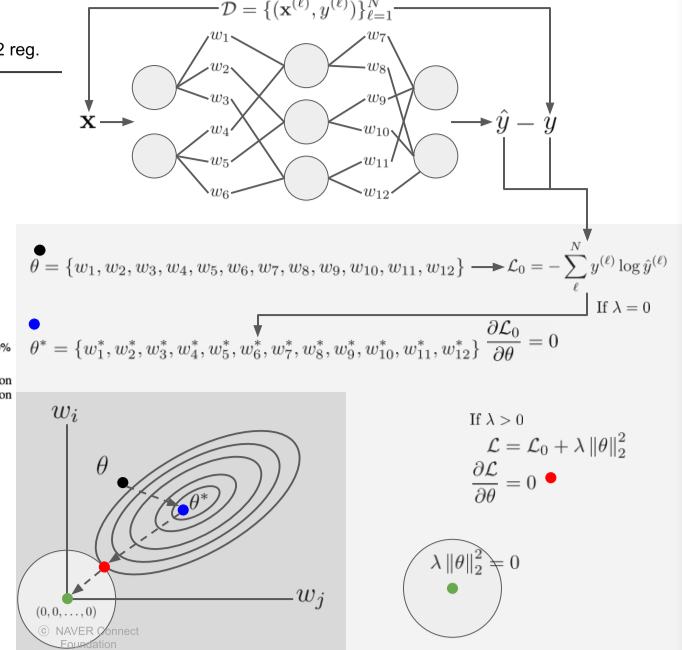
[img. Pruning시, Iterative하게하고, retrain을 하면 성능을 좀더 보존할 수 있다.]
[img. Regulariazation에 대한 설명]
여러가지 Pruning들
Pruning 방법은 분류에 따라 아주 많다
- Global Magnitude Pruning, Layerwise Magnitude Pruning, Random Pruning 등등…
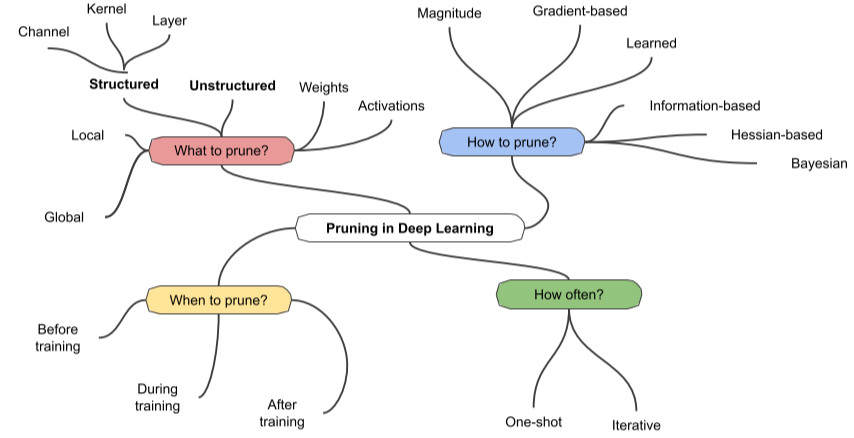
[img. Prunning의 분류 방법]
Unstructured VS Structured Pruning
Unstructured pruning은 weight 연산을 구분없이 사라지게 하며
- Neuron이 성긴 모양으로 생기게 되는 장점
Structured pruning은 커널이나, Layer 등의 구분을 두고, 해당 구분에서 통째로 사라지게 만든다.
- 하드웨어 등에서 좀더 잘 Pruning 해준다.
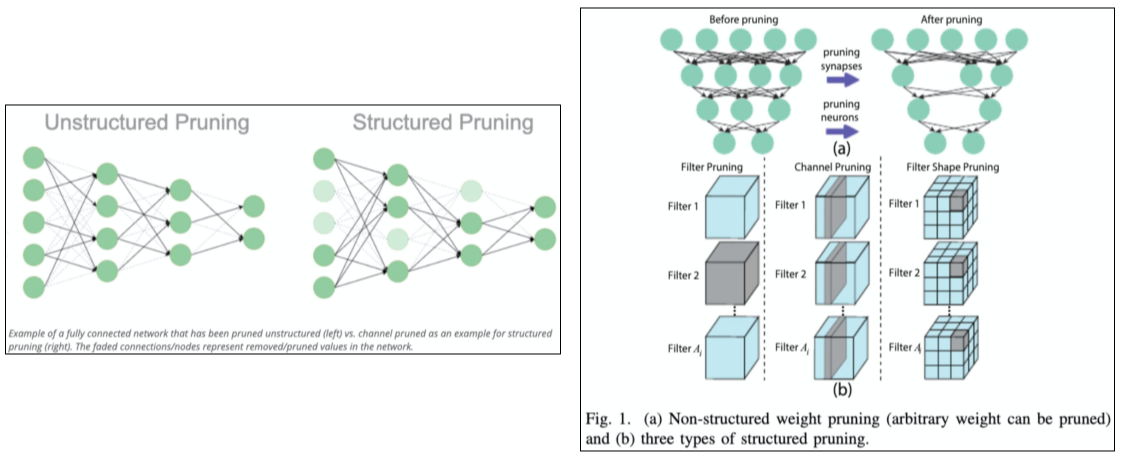
[img. Unstructure Pruning vs structured pruning]
Scratch-trained는 시작부터 다시 트레이닝 하는 거며,
Fine tuning은 Pretraing 된 것을 pruning 한것,
Unstructed Pruning은 Finetuning을 하여도 0 주변 weight가 되살아나지 않는다.
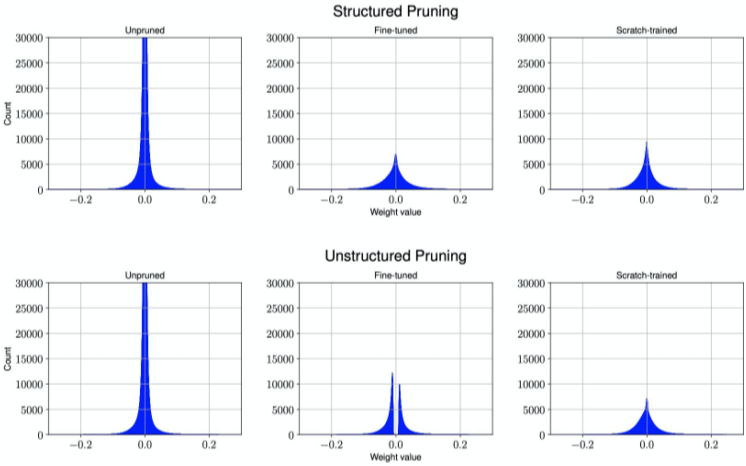
[img. 두 방법의 결과 그래프]
한꺼번에 Pruning 하면 Retraining 해도 Accuracy가 다시 오르지 않는다고 한다.
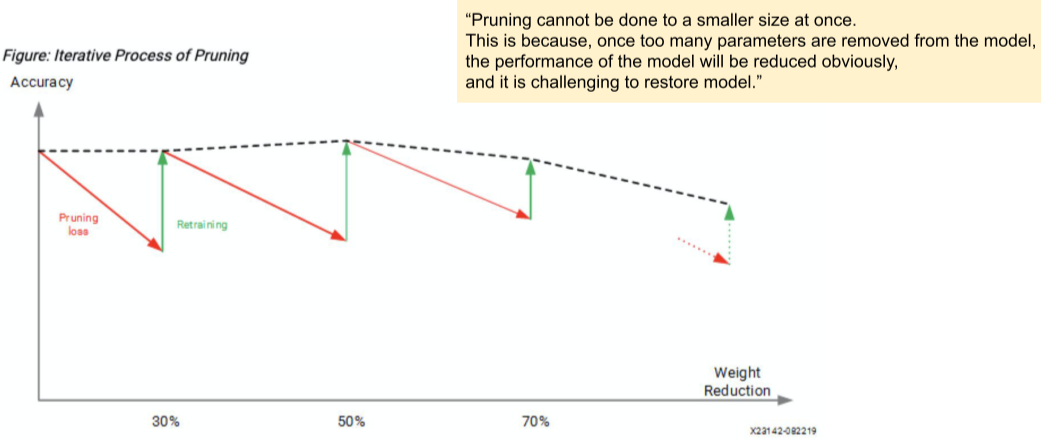
[img. 한꺼번이 아니라 조금씩 pruning한 결과]
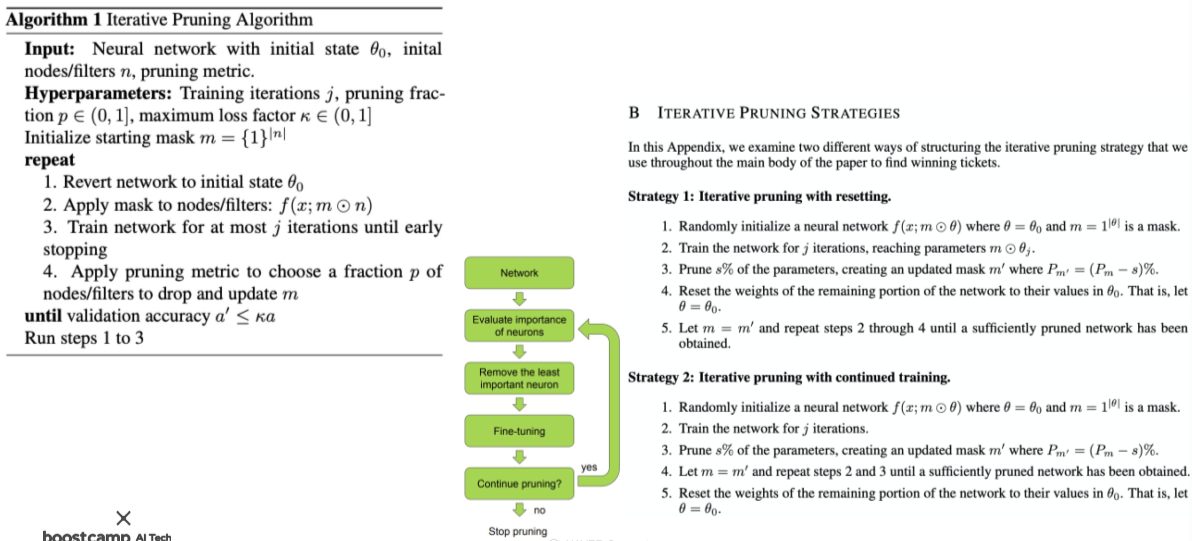
[img. 자세한 Pruning 과정]
Lottery Ticket Hypothesis
Lottery Ticket Hypothesis란, 같은 accuracy를 가진 Pruning한 network가 원래 기존의 원본 network 안에 subnetwork로 존재했을 것이라는 가설.
즉, 굳이 Pruning을 하지 않아도 처음부터 Pruning한 network 구조를 알 수 있으면 처음부터 Pruning한 Network(Lottery ticket)를 가지고 올 수 있다.
가설이므로 아직 증명은 안됨

[img. Lottery Ticket Hypothesis에 대한 개념]
retraining시 처음 Initial state의 W로 시작하지 않고, 어느정도 train된 $W_k$부터 시작하는 방법,
랜덤화를 위해 조금의 noise를 섞어준다.
어느 정도 training 구간을 skip 할 수 있으므로 training cost를 줄이면서 성능도 좋아진다.
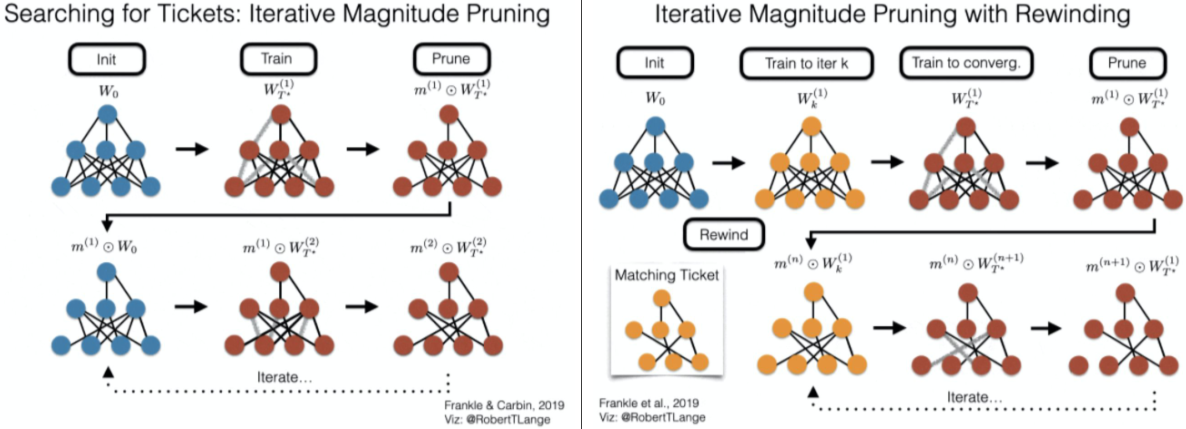
[img. Lottery Ticket을 구하는 방법 중 하나인 Rewinding]

[img. Rewinding algorithm]
양자화 (Quantization for model compression)
Fixed point, floating point
32-bit fixed-point는 앞에 지수 10자리를 정수부분, 뒤의 22 자리를 소수점을 표현하는데 사용
- 덧셈과 뺄셈시 erorr가 없음, 정수 분수 표현 가능
-
연산 속도가 빠르고 메모리 사용량, 전력 사용량이 적음
- 곱셈이 힘들고(수가 자주 표현범위를 넘어가므로), 수의 표현 범위가 작음
32bit floating-point는 가수부에서 일의 자리 + 소수점 부분을 표현하며, 앞의 지수부에서 10의 지수를 표현함
- 비교적 많이 사용되며, 아주 넓은 범위의 수를 손실없이 표현 가능
- hardware에 구현이 힘듦, 특히 ARM에서 구현 힘듦
- 과거에는 FPU(Floting point precessing unig)라는 CPU와 별개의 연산 장치가 연산했지만 요즘에는 CPU에 내장
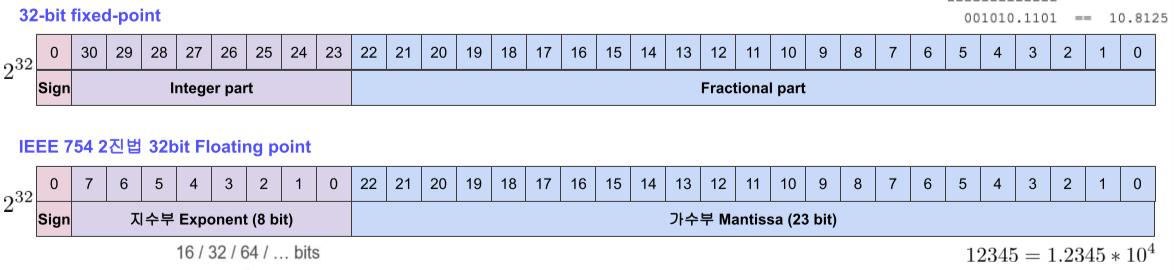
[img. fixed-point vs floating point]
소수점 연산은 수가 단계에 맞아떨어지는 정수와 달리 연속적인 수이므로 연산이 힘들고 복잡하다.
Quantization의 아이디어는 float으로 이루어진 AI weight를 연산이 빠른 정수형으로 바꾸는데에 있다.
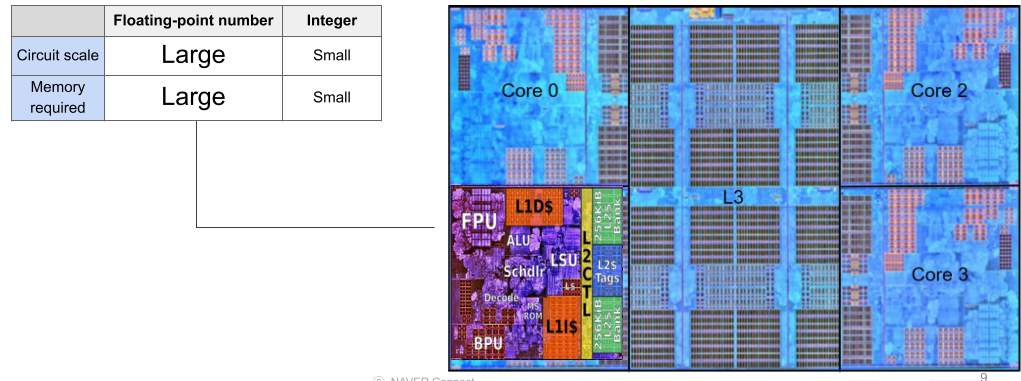
[img. 소수점 연산의 힘듦 : CPU 내의 FPU의 크기]
정확도 vs 정밀도
정확도(Precision) : 정답과 값들의 거리
정밀도(Variance) : 값 간의 모임 거리
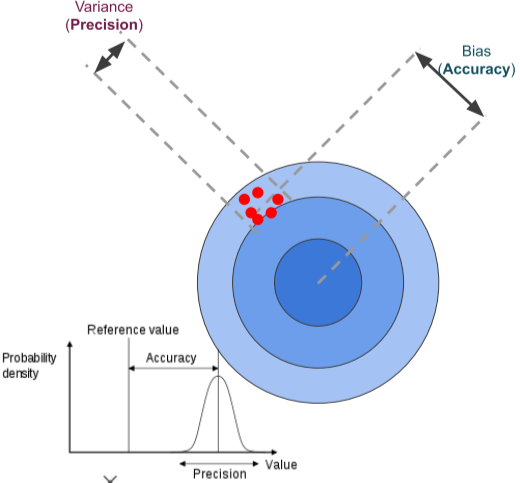
[img. Variance vs bias]
양자화(Quantization)
모델크기 감소, Inference 시간 감소에 효과적이며, 메모리 bandwidth 요구에 맞추는데 사용
기존에 float32형태의 weight 값들에서 int8형으로 mapping하여 속도의 향상을 얻을 수 있다
대신 lossy conversion이므로 정보가 조금 손실된다.
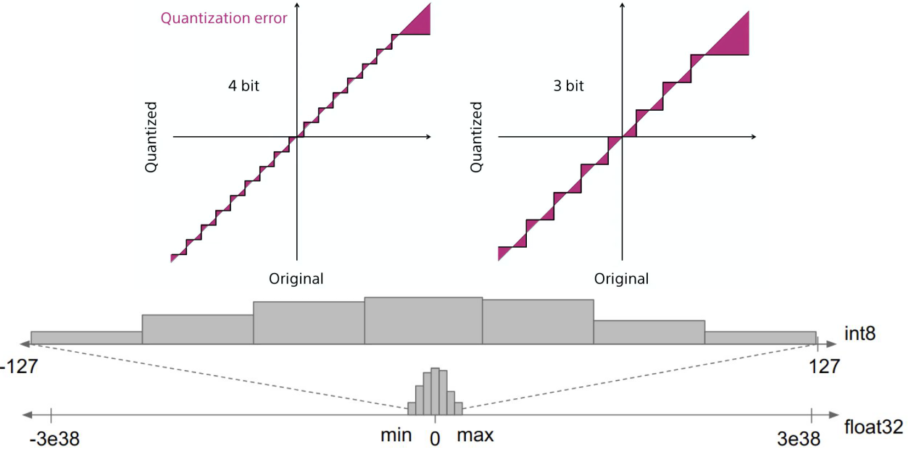
[img. 8비트 정수값에 맞게 mapping한 Quantization(아래)과 그에 따른 에러 그래프(위)]
[img. Deep Learning은 아주 많은 compuation을 필요로 한다.]
Affine quantization
Affine transformation : 공간 dimension이나 평행 선의 길이의 비율(parallel line segemnt)은 유지한채로 affine space로 변환하는 변환
모양은 유지한 채로, 비율만 변하는 변환? “닮음 변환”
Affine map은 결합 법칙이 성립함 $m_f(x-y)=f(x)-f(y)$
ex) $y=\sigma\left(\sum_{i=1}^nx_iw_i + b\right): ML의\ 선형변환의\ Activation\ 적용\ 전까지$
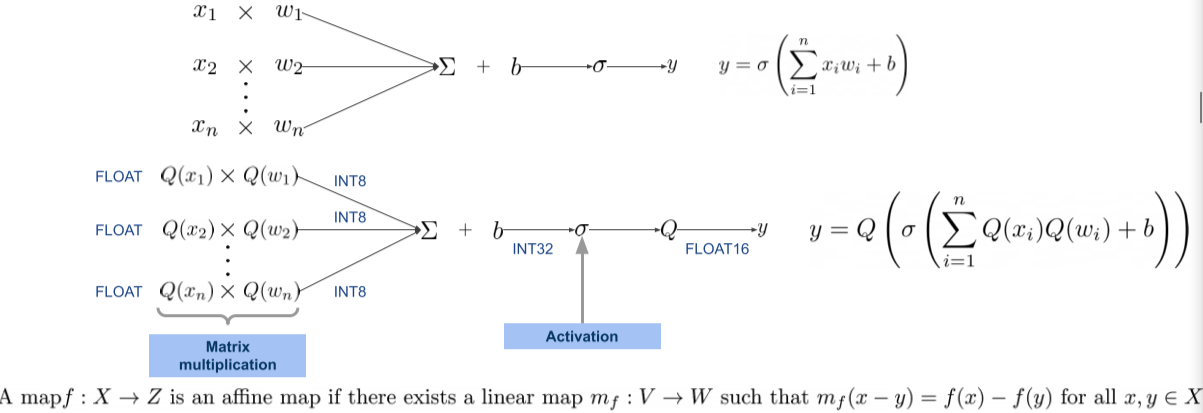
[img. Affine quantization의 예시]

[img. Quantization mapping의 과정]
Quantizing activation and weights
Weight뿐만 아니라 Activation또한 Quantization이 가능하다.
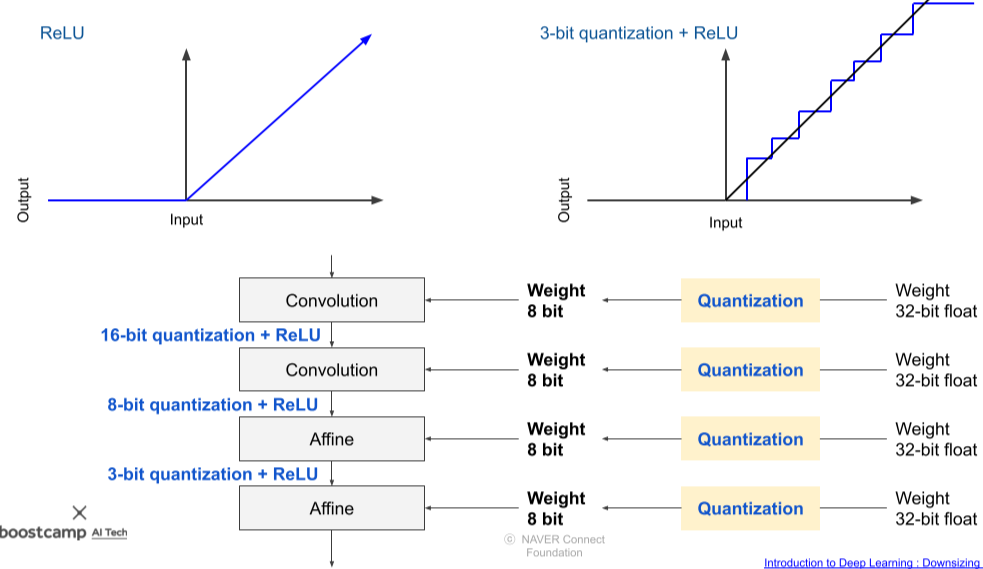
[img. 정수값마다 계단형으로 바뀐 activation]
하지만 Activation을 Quantization할 경우, Backpropagation 시 문제가 생긴다.
이를 해결하기 위해,
1) 계단식의 그래프와 가장 비슷한 기울기 1의 그래프로 쳐서 Backpropagation 한다.
2) 또는, Quantization을 할 때 smothing을 주어 미분가능한 형태로 만든다.
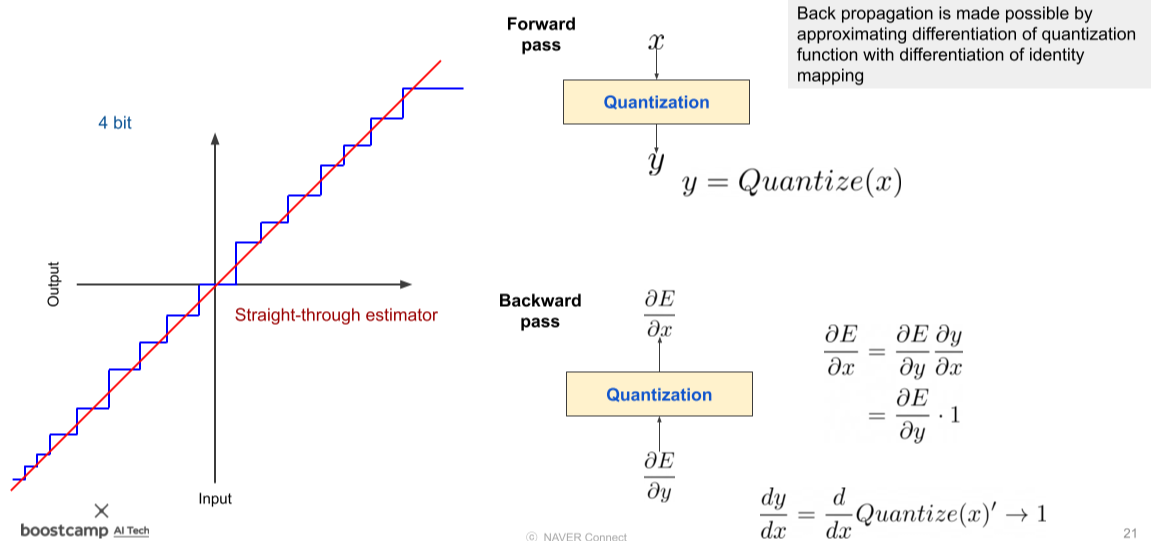
[img. Quantization에 의한 Backpropagation 문제 해결 1]
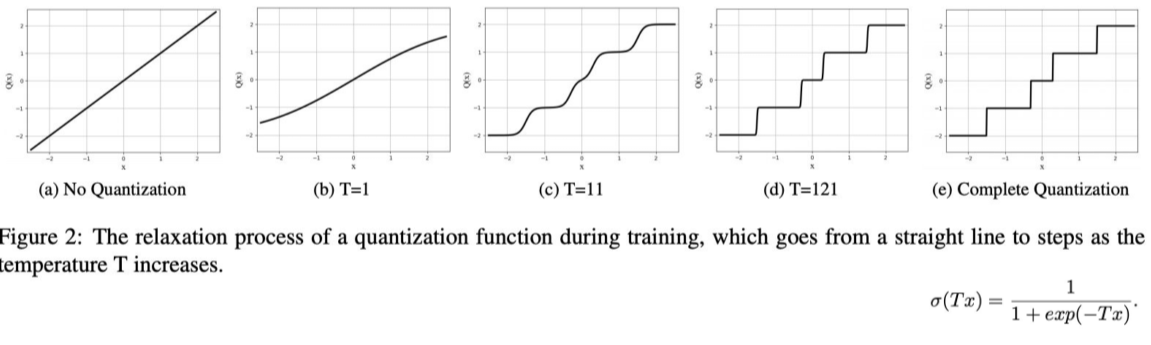
[img. Quantization에 의한 Backpropagation 문제 해결 2]
DoReFa-Net style 3-bit activation quantizer function 이나
Binarized Neural Networks 처럼
8단계(3bit)나 극단적으로 1bit(0,1)로만 activation을 바꾸는 방법도 있다.
Quantization의 종류
- Quantization 대상에 따라 : Weight, Activation
- Quantize 방법에 따라 : Dynamic(DQ, Acitvation들을 Inference 할 때 그 순간만 양자화, Weight는 처음부터 양자화 ), Static(양자화된 채로 아예 변형)
- Quantize 강도에 따라 : 1bit~16bit, Mixed-precision
- Quantize 시기에 따라: Post-training(PTQ, Training된 모델에 Quantize, 파라미터 size가 클수록 성능 하락 적음), Quantization aware training(QAT, Training 하면서 Quantization을 시뮬레이션, 성능하락 적음)
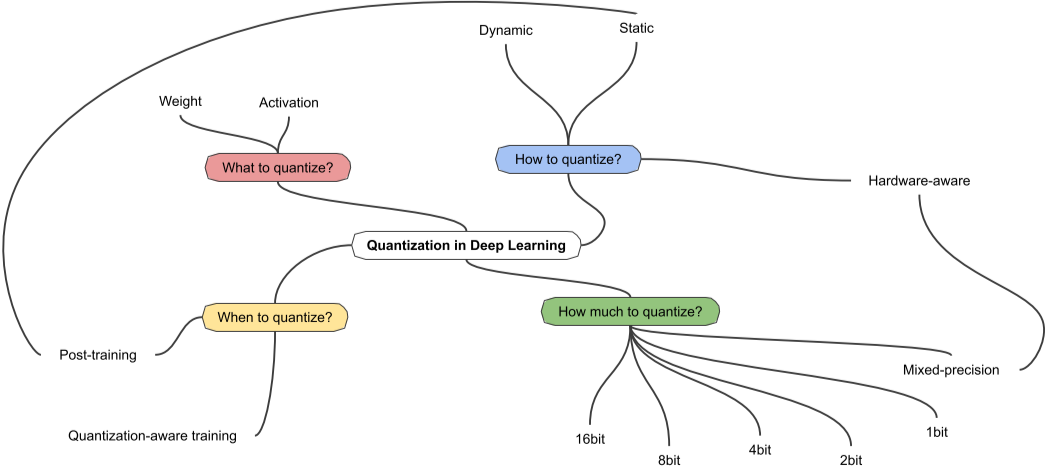
[img. Quantization의 종류 구분]
DQ, PTQ, QAT 모두 원본 Model과는 성능이 똑같지 않다.
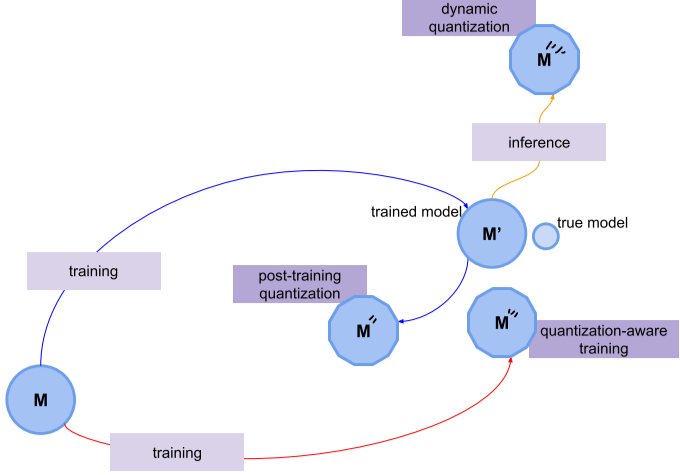
[img. DQ, PTQ, QAT에 대한 도식]
GPU, TPU 등의 큰 분류 뿐만 아니라, 제조사, 제조 모델, 운영체제나 라이브러리에 따라 지원하지 않을 수도 있다.
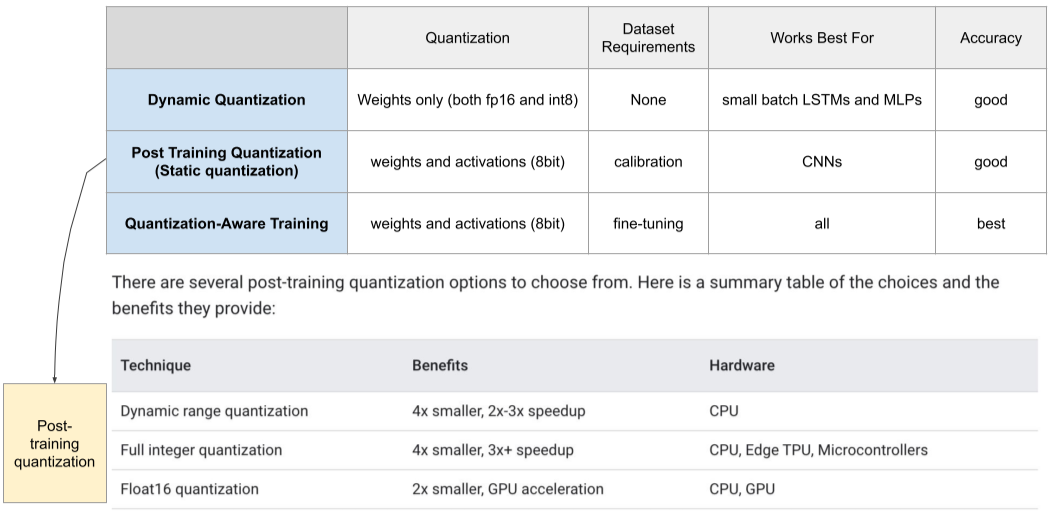
[img. Quantization 들의 장점과 하드웨어 제한]
[img. 여러가지 방법을 섞어서 Quantization을 할 수 있다.]
Hardware-aware-quantization
하드웨어에 따라 가능한 Quantization 방법이 다르고, 적절한 방법도 다르다.
강화학습과, 성능 측정을 통해 하드웨어 적합한 Policy를 찾아 적용 가능하다.
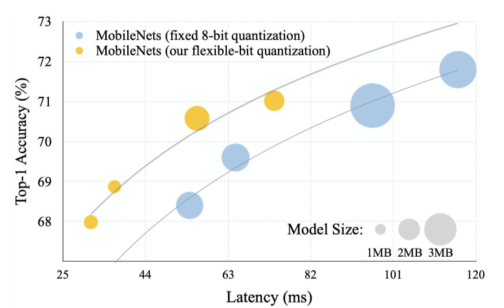
[img. bit 크기에 따른 quantization의 성능 비교]
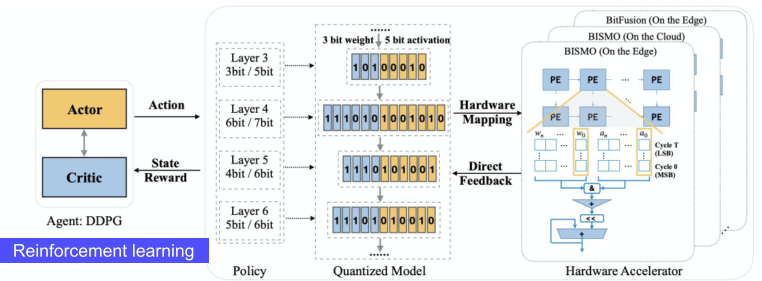
[img. 강화학습을 이용한 Hardware-aware quantization]
Quantization 결과 테이블 읽기
주로 여러가지 방법의 Quantization 간의 Latency와 용량, accuracy를 비교해본다.
Resnet의 경우 Batch Normalization layer 때문에 안되는 것으로 추정
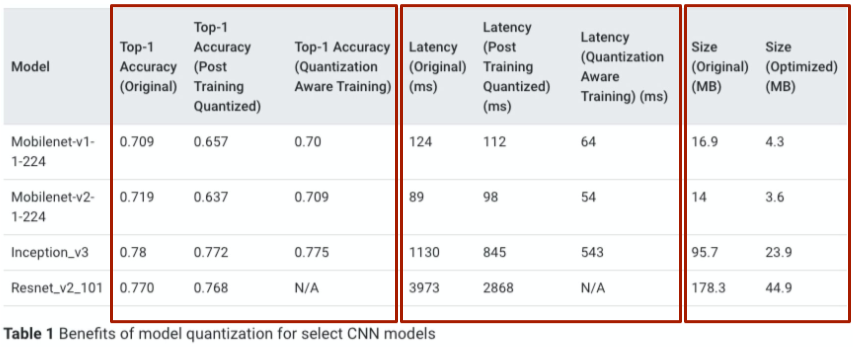
[img. Quantization 결과]
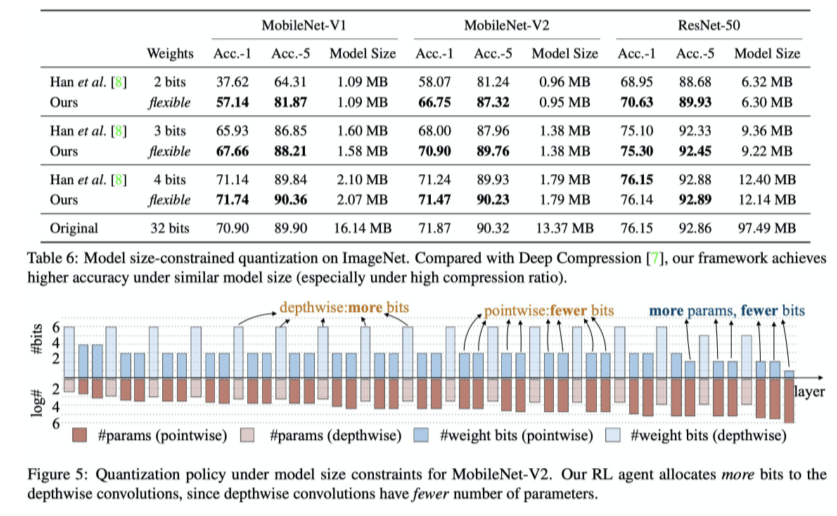
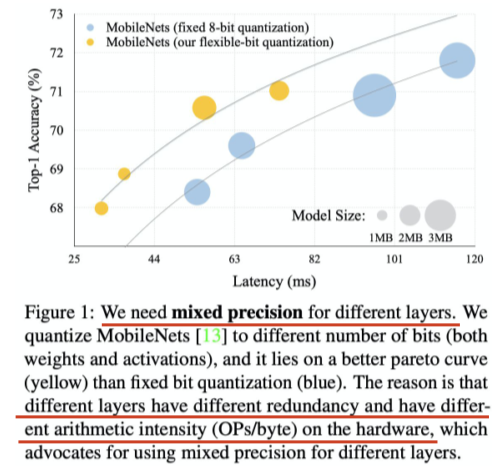
[img. Flexible bit를 이용한 Quantization 결과 비교 예시]
지식 증류 (Knowledge distillation for network compression)
Knowledge
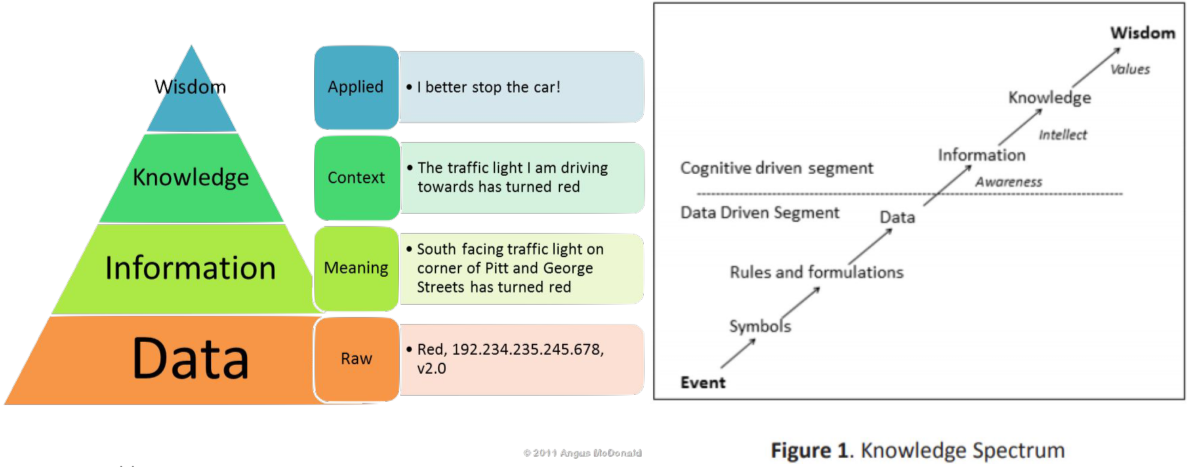
[img. Knowledge의 정의]
$C_K$는 Reference class(모든 확률을 더한 값?)
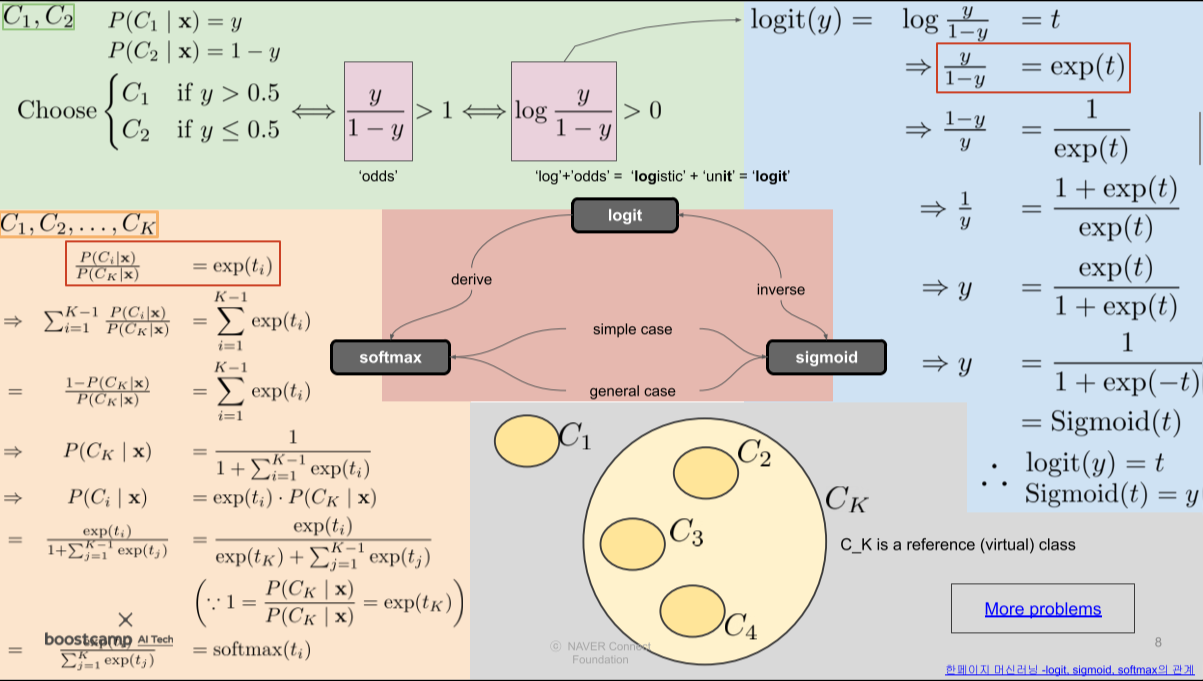
[img. logit, softmax, sigmoid의 정의]
Knowledge distillation
training 시와 deploment 간 필요한 setting과 parameter가 다르다.
그러므로 deploy를 위한 compressed된 model이 따로 필요하다.
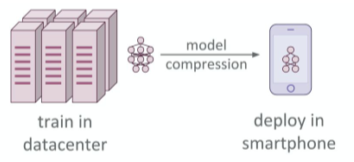
[img. train model과 deploy 모델 차이]
Transfer learning은 다른 도메인의 모델을 Task를 위해 기존의 모델을 통해 learning 하는 것이며,
Teacher-Student model은 같은 도메인 내에서 model size를 줄이기 위해 Learning 한다.

[img. knowledge distillation 방법 중 하나인 Teacher-student model]
Teacher-Student networks & Hinton loss
Teacher-student 모델로 생성된 최적화된 모델은 데이터에서 직접 트레이닝한 모델보다 비슷한 크기, 비슷한 파라미터 하에, 성능이 더 좋은 경향이 있다.
Teacher의 결과와의 차이인 distllation loss와 Ground-Truth와의 차이인 student loss를 합쳐서 종합 Loss(Hinton loss)를 만든다.
이때 $p_i$를 통하여 결과값인 class별 확률을 soft하게 만들어준다.
- $p_i$의 T는 Temperature로 knowledge distillation의 핵심이다.
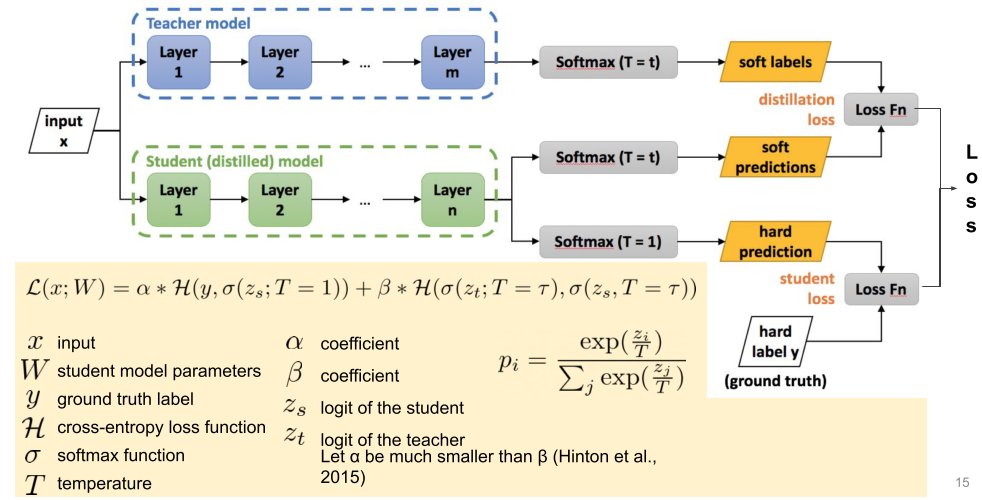
[img. Teacher-Student 모델의 개념도]
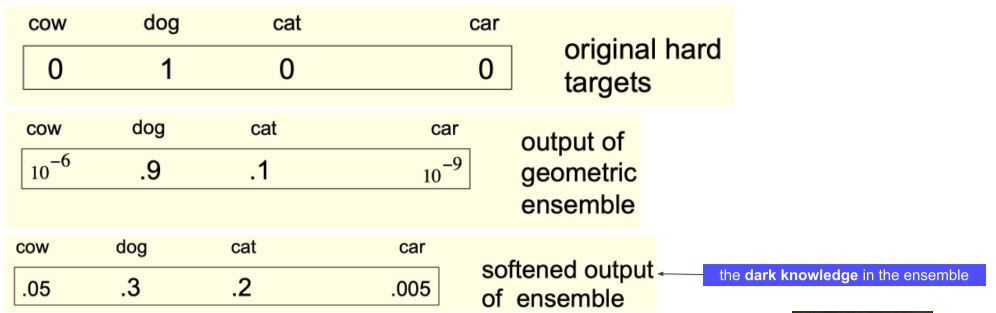
기존의 one-hot vector의 경우나, 확률 편차가 극도로 큰 ouput은 정보가 많이 없는 반면,
soften한 output의 경우, 개와 고양이의 정보값이 큰것으로 보아, 개와 고양이를 조금 헷갈려 한다는 것을 알 수 있다.(Dark knoweldge)
이 정보를 이용하기 위해 결과값을 soften 한다.
- 다 합쳐서 1이 되는 것은 모두 같아야 한다, 아래 그림은 나머진 숨긴 것
[img. 결과값을 soft하게 하는 이유]
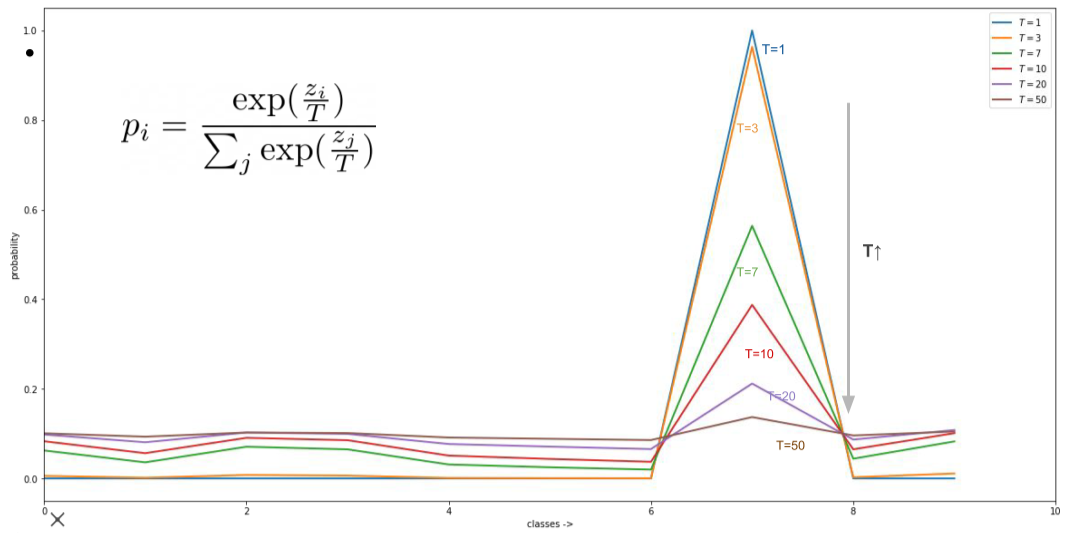
[img. T의 크기에 따른 softmax output]
Zero-mean assumption
knowledge distillation == model compression이 되려면 zero-mean Assumption이 True여야 한다.
zero-mean Assumption이란, logit들이 모두 Zero-mean일 경우를 의미한다.
\(\frac{\partial C}{\partial z_i}=\frac{1}{T}(q_i-p_i)=\frac{1}{T}\left(\frac{e^{z_i/T}}{\sum_je^{z_j/T}}-\frac{e^{v_i/T}}{\sum_je^{v_j/T}}\right)
\\\approx\frac{1}{T}\left(\frac{1+z_i/T}{N+\sum_jz_j/T}-\frac{1+v_i/T}{N+\sum_jv_j/T}\right)\\
\approx \frac{1}{NT^2}(z_i-v_i) : compression\\
z_i:distilled\ model\ logits, v_i:teacher\ model\ logits\)
[math. zero-mean assumption이 참이 되어야 성립하는 식]
여러 distillation들
이외에도 여러 distillation 방법들이 존재한다.
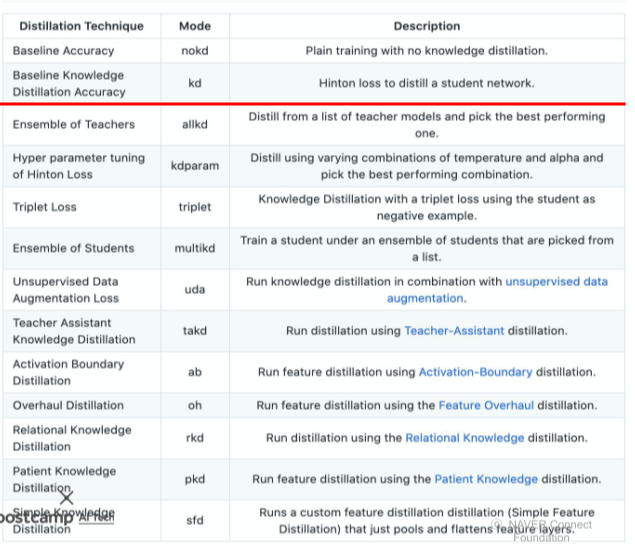
[img. 여러 distilation 기법, 우리가 배운 것은 밑줄 친 BLKL]
예를 들자면,
Overhaul Feature Distillation
- 중간에 Distillation 상황을 점검하고 결과값을 비교하는 Layer을 추가,
- feature를 뽑는 distillation output의 위치 ReLU이전으로 조정,
- partial L2 distance 제안
Data-Free Knowledge Distillation
- 데이터가 적거나 없을 때 사용할 수 있는 방법
- meta data로 data를 reconstruction 하여 사용함
- Pruning, Quantization, Matrix factorization 등의 방법도 data-free임.
행렬 분해(Low-rank approximation for model compression)
Three maps
- Matrix 또는 Tensor는 data modeling tool 이다.
Matrix와 달리 Tensor는 2차원 이상의 Matrix를 의미함.

[img. Matrix 또는 Tensor의 해석 방법 ]
- Matrix(Tensor)는 linear transformation(선형 변환) (map)

[img. 차원공간에서의 위치 변경이 가능함]
- terminology

[img. 행렬에 대한 전문용어]
행렬을 통하여 연립방정식 또한 표현 가능하다.
\(\left\{\begin{matrix}
x+2y+z=5\\-2x-3y+z=8 \\3x+5y+0z=2 \\
\end{matrix}\right. \Leftrightarrow \begin{bmatrix}
1 & 2 & 1\\
-2 & -3 & 1\\
3 & 5 & 0
\end{bmatrix}\begin{bmatrix}
x
\\
y
\\
z
\end{bmatrix}=\begin{bmatrix}
5
\\
8
\\
2
\end{bmatrix}\)
[img. 연립방정식의 행렬에 의한 표현]
Gaussian elimination
basis : n차원 공간을 결정하기 위한 n개의 벡터의 집합을 basis라고 한다고 함.
rank + nullity로 matrix의 dimension을 구할 수 있음

[img. Rank를 구하는데 사용]

[img. filter, matrix, tensor의 처리 방법]
Low-rank matrix approximations : large-scale learning problem kernel method에 필요한 툴
Kernel method
kernel: a central or essential part

[img. CNN에서의 Kernel]
kernel method를 통하여 고차원으로 변환할 때 연산량을 줄일 수 있다.
- 저차원에서 내적값을 미리 계산한 뒤, 변환

[img. kernel method의 고차원 변환에서의 사용]

[img. kernel method의 적용 연산 비교]
연산량이 줄어들지만 연산결과가 완전 같지는 않다.
optimization에서 많이 사용함


[imgs. ML에서 low-rank approximation을 이용한 파라미터 감소 예시]
Matrix decomposition
행렬을 n개의 행렬의 곱으로 나타내는 것,
approx 값일 때도 있고, equal 값일 때도 있다.
ML이전에 PCA, SVD 등을 이용한 추천 시스템 등에서 많이 사용함

[img. Matrix decomposition의 예시]
Eigen Vector: 변환 시켰을 때, 길이만 변하는 벡터
Eigen Value: 변환 시켰을 때, 길이만 변하는 벡터가 변한 길이의 량
위 두 개념을 이용해 행렬을 변환시킬 수 있다.

[img. Eigenvalue Decomposition]
Singular value decomposition (SVD): a generalization (nm case) of EVD
가로 세로 길이가 다른 행렬을 가로 세로 길이를 뒤바꾼 형태로 transpose하여, 정행렬과 정행렬의 transpose, 그리고 singular value의 제곱($\sum^2_{nn}$= Eigen value)으로 나타내는 방법
다항식의 인수분해로 비유할 수 있음

[img. SVD 예시]

[img. SVD를 이용한 PCA 차원축소]

[img. 다양한 방식의 decomposition]
Tensor decomposition

[img. Tensor의 예시]
각각 다차원 matrix나 tensor는 outer product를 통해 rank 1 짜리 matrix나 tensor로 표현 가능

[img. Matrix decomposition]
CP (Canonical Polyadic) decomposition
tensor 버전의 SVD (Rank1 짜리 tensor의 linear combination 표현)
Tucker의 경위 CP의 일반화된 버전 (Rank 1은 아니지만 조금더 저차원의 tensor로 표현)
두뇌의 신경 구조 분석 등을 위해 사용

[img. CP의 예시]
Tensor decomposition on network compression
모바일넷의 선형대수적 증명과 모바일넷 v2의 차이에 관한 논문에 대한 설명
network compression은 위에서 설명한 decomposition을 이용해 설명할 수 있는 경우가 많다.
_articles/AI/Lightweight/모델 경량화 기본.md