풀스택 웹🌐 개발자 지망생 🧑🏽💻
➕ 인공지능 관심 🤖
Categories
-
┣
▶ COMPUTER_SCIENCE
📂: 7 -
┣
▶ WEB
📂: 3 -
┣
▶ ETC
📂: 3-
┃
┣
ETCS
📄: 10 -
┃
┣
SUBBRAIN 개발기
📄: 5 -
┃
┗
YOS 개발기
📄: 1
-
┃
┣
-
┗
▶ AI
📂: 9-
┣
AITOOLS
📄: 3 -
┣
CV
📄: 2 -
┣
DEEP_LEARNING
📄: 1 -
┣
DATA_VIS
📄: 2 -
┣
GRAPH
📄: 1 -
┣
LIGHTWEIGHT
📄: 1 -
┣
MATH
📄: 1 -
┣
NLP
📄: 3 -
┗
STRUCTURED_DATA
📄: 2
-
┣
그래프 기본
- Graph Introduction
- 그래프를 이용한 기계학습
- 페이지 랭크 알고리즘
- 그래프를 이용한 바이럴 마케팅
- 그래프 군집 구조
- 추천 시스템
- 그래프의 벡터 표현
- 추천 시스템 심화
- 그래프 신경망(Graph Neural Network) 기본
- 그래프 신경망 심화
그래프(Graph) 기본
네이버 boostcamp AI Tech의 강의를 정리한 내용입니다
정점 집합과 간선 집합으로 이루어진 수학적 구조로, 다양한 복잡계(Complex Network)를 분석할 수 있는 언어
Graph Introduction
Graph란 무엇이고 왜 중요할까?
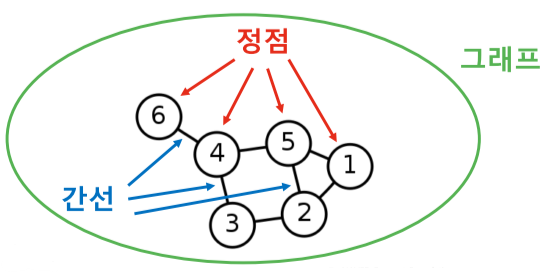
[img. 정점과 간선, 그래프의 그림]
- 정점(Vertex) : 노드(Node)라고도 불림. 관계를 가지거나 가지지 않는 하나의 객체
- 간선(Edge): 링크(Link)라고도 불림. 두 개의 정점을 연결하는 선
- 그래프(Graph): 네트워크(Network)라고도 불림. 정점 집합과 간선 집합으로 이루어진 수학적 구조
우리의 주변에는 친구관계, 통신, 인터넷과 같은 많은 구성 요소 간의 복잡한 상호작용인 복잡계(Complex System)이 있으며, 그래프는 이 복잡계를 표현하고 분석하기 위한 언어이다.
그래프 관련 인공지능 문제
- 정점 분류(Node Classification) 문제 : 정점의 특성, 연결에 따라 분류할 수 있는가?
- 트위터의 공유 관계를 분석하여 사용자의 정치적 성향 판단
- 연결 예측(Link Prediction) 문제: 앞으로 그래프의 성장이 어떻게 될 것인가?
- 페이스북 소셜 네트워크는 어떻게 진화할까?
- 추천(Recommendation) 문제: 한 정점이 어떠한 경향으로 간선을 만드는가?
- 상품, 영화 추천
- 군집 분석(Community Detection) 문제: 연결 관계로부터 사회적 무리(Social Circle)을 찾아낼 수 있을까?
- 연결 관계를 통한 가족 관계, 친구 관계, 대학 동기 들의 무리를 찾아내기
- 랭킹(Ranking) 및 정보 검색(Information Retrieval) 문제: 그래프 내부에서 찾고 싶은 정점 찾기
- 웹이라는 거대한 그래프로부터 찾고자 하는 웹페이지를 찾아내는 법
- 정보 전파(Information Cascading) 및 바이럴 마케팅(Viral Marketing) 문제: 어떻게 최대한 간선을 통하여 전파 시킬 수 있는가?
- 마케팅, 홍보 문제
그래프 관련 필수 기초 개념
그래프의 유형 및 분류
| 명칭 | 무방향 그래프(Undirected Graph) | 방향 그래프(Directed Graph) |
|---|---|---|
| 설명 | 간선엔 방향이 없는 그래프 | 간선엔 방향이 있는 그래프 |
| 예시 | 협업 관계 그래프, 페이스분 친구 그래프 등 | 인용 그래프, 트위터 팔로우 그래프 |
| 그림 | 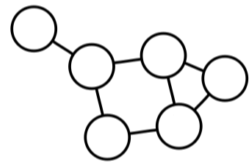 |
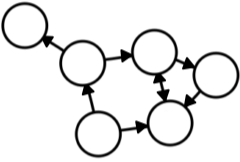 |
[fig. 방향성에 따른 그래프 분류]
| 명칭 | 가중치가 없는 그래프(Unweighted Graph) | 가중치 그래프(Weighted Graph) |
|---|---|---|
| 설명 | 간선에 가중치가 없는 그래프 | 간선에 가중치가 있는 그래프 |
| 예시 | 웹 그래프, 페이스북 친구 그래프 | 전화 그래프, 유사도 그래프 |
| 그림 |  |
 |
[fig. 가중치 여부에 따른 그래프 분류]
| 명칭 | 동종 그래프(Unpartite Grpah) | 이종 그래프(Bipartite Graph) |
|---|---|---|
| 설명 | 동종 그래프는 단일 종류의 정점만 포함 | 두 종류의 정점을 가지는 그래프, 다른 종류의 정점 사이에만 간선이 연결됨. |
| 예시 | 웹 그래프, 페이스북 친구 그래프 | 전자 상거래 구매 내역(사용자, 상품), 영화 출연 그래프(배우, 영화) |
| 그림 |  |
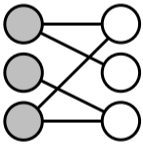 |
[fig. 정점의 종류에 따른 그래프 분류]

[fig. 방향성이 없고 가중치가 있는 이종 그래프의 예시]
그래프 관련 필수 기초 개념

[img. 그래프]
보통 정점들의 집합을 V, 간선들의 집합을 E, 그래프를 G = (V,E)로 표현
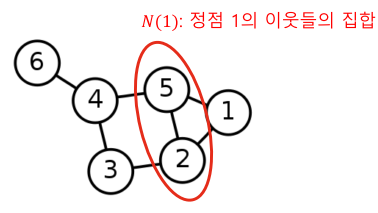
[img. 정점 1의 이웃 집합]
정점의 이웃(Nieghbor)은 그 정점과 연결된 다른 정점을 의미하며 v의 이웃 집합을 보통 N(v) 혹은 $N_v$로 표기, 위 그림의 경우 N(1) = {2,5}
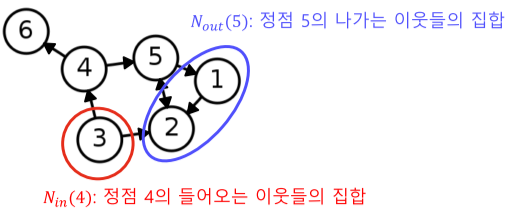
[img. 방향 그래프에서의 이웃]
방향성이 있는 그래프에서는 나가는 이웃과 들어오는 이웃을 구분하며,
- 정점 v에서 간선이 나가는 이웃(Out-Neighbor)의 집합을 보통 $N_{out}(v)$로 표기
- 정점 v에서 간선이 들어오는 이웃(In-Neighbor)의 집합을 보통 $N_{in}(v)$로 표기
- 그림의 경우, $N_{out}(5)={1,2},\ N_{in}(4)={3}$
그래프의 표현 및 저장
- NetworkX 그래프 Vis 코드 + 간선 저장 코드의 경우 LAB의 [Graph-1]Grpah_Basic.ipynb 참조
- 간선 리스트(Edge List) : 그래프를 간선들의 리스트로 저장
- 정점 간의 간선 유무를 알아보기 위해 모든 리스트를 다 확인해봐야함, 성능상 비효율적임.
| 무방향성 | 방향성 |
|---|---|
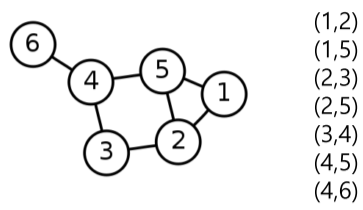 |
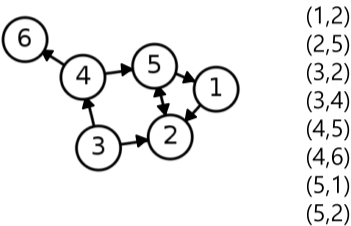 |
| 간선이 연결하는 두 정점들의 순서쌍(Pair)로 저장 | 방향성이 있는 경우에는 (출발점, 도착점) 순서로 저장 |
[fig. 간선리스트의 예시]
- 인접 리스트(Adjacent list) : 정점들의 이웃들을 리스트로 저장
- 간선 리스트에 비해 성능상 효율적임
| 그래프 | 도식 | 설명 |
|---|---|---|
| 무 방향성 | 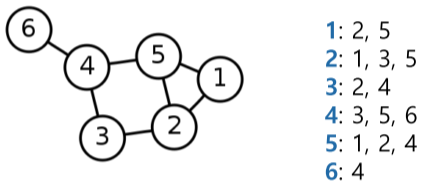 |
각 정점의 이웃들을 리스트로 저장 |
| 방향성 | 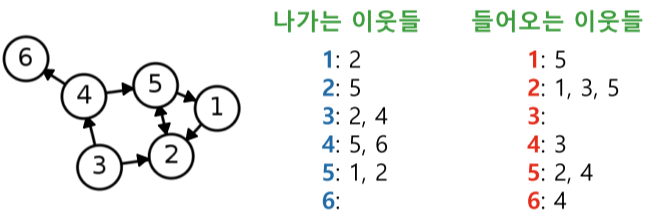 |
각 정점의 나가는 이웃들과 들어오는 이웃들을 각각 리스트로 저장 |
[fig. 인접리스트의 예시]
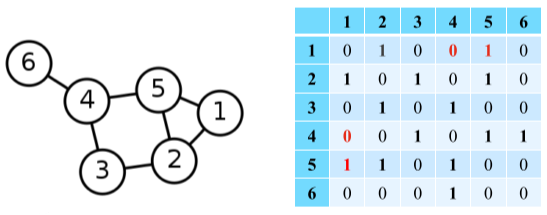
- 인접 행렬(Adjacency Matrix)
- 연산 성능 상 문제 없고 구현이 쉽지만 메모리 낭비가 심하다.
| 무방향성 | 방향성 |
|---|---|
 |
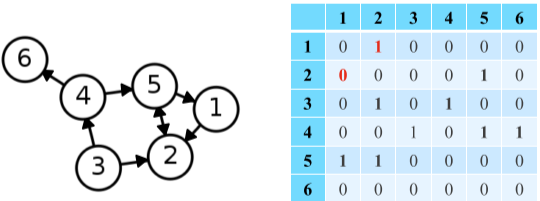 |
| 정점 수 $\times$ 정점 수 크기의 행렬 | 정점 수 $\times$ 정점 수 크기의 행렬 |
| 정점 i 와 j 사이에 간선이 있는 경우, 행렬 (i, j) 그리고 (j, i) 원소가 1 없는 경우 0 | 정점 i 에서 j 로 가는 간선이 있는 경우, 행렬 (i, j)가 1 없는 경우 0, 반대로, 정점 j에서 i로 가는 간선이 있는 경우, 행렬 (j,i)가 1 없는 경우 0 |
[fig. 인접 행렬의 예시]
그래프를 이용한 기계학습
실제 그래프 vs 랜덤 그래프
실제 그래프(Real Graph)란 다양한 복잡계로 부터 얻어진 그래프를 의미
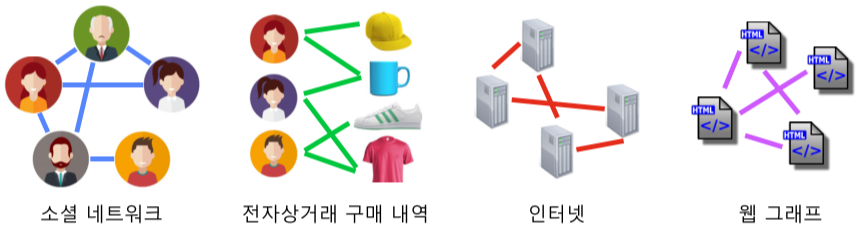
[img. 실제 그래프의 예]
랜덤 그래프(Random Graph)는 확률적 과정을 통해 생성한 그래프를 의미
- 에되스-레니 랜덤 그래프(Erdos-Renyi Random Graph) : $G(n,p)$
- n 개의 정점을 가짐
- 임의의 두 개의 정점 사이에 간선이 존재할 확률은 p, 모든 정점 사이가 동일함
- 정점 간의 연결은 서로 독립적(Independent)
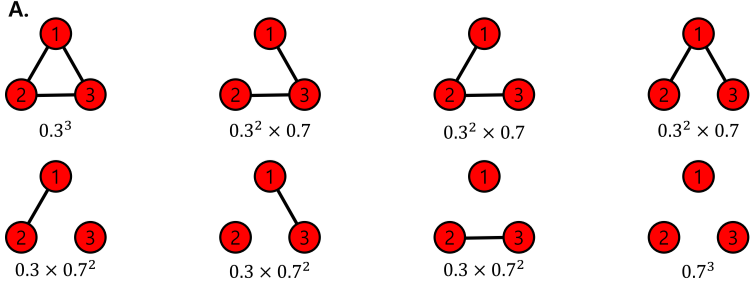
[img. $G(3,0.3)$일때 생성될 수 있는 그래프와 확률]
작은 세상 효과
| 개념 | 설명 |
|---|---|
| 경로(Path) | 첫번째로 u에서 시작해서 정점 v에서 끝나야 하며, 두번째로, 순열에서 연속된 정점은 간선으로 연결되어 있어야 함. |
| 경로의 길이 | 경로 상에 놓이는 간선의 수로 정의됨 |
| 정점 사이의 거리(Distance) | u와 v 사이의 최단 경로의 길이 |
| 최단 경로(Shortest Path) | u와 v사이의 거리가 최소가 되는 경로 |
| 그래프 지름(Diameter) | 정점 간 거리의 최댓값 |
[fig. 그래프의 개념 설명]
| 그래프 | 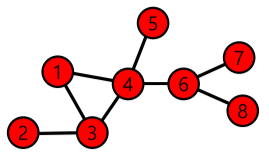 |
|---|---|
| 경로 예시 | 정점 1과 8사이의 경로는 [1,4,6,8], [1,3,4,6,8],[1,4,3,4,6,8] |
| 경로 길이 예시 | 경로 [1,3,4,6,8]의 길이는 4 |
| 거리 예시 | 정점 1과 8 사이의 최단 경로는 [1,4,6,8]로 거리는 3 |
| 지름 예시 | 정점 2에서 8까지 4 |
[fig. 그래프의 개념 예시]
작은 세상 효과(Small-world Effect) : 실제 그래프의 임의의 두 정점 사이의 거리는 생각보다 작다.
- 여섯 단계 분리(Six Degrees of Separation) 실험에서 6단계 만에 오마하에서 보스턴까지 편지를 전달
- MSN 메신저 사용자의 평균 거리는 7
- 랜덤 그래프에도 존재하지만 체인(Chain), 사이클(Cycle), 격자(Grid) 그래프에서는 작은 세상 효과가 존재 하지 않음.
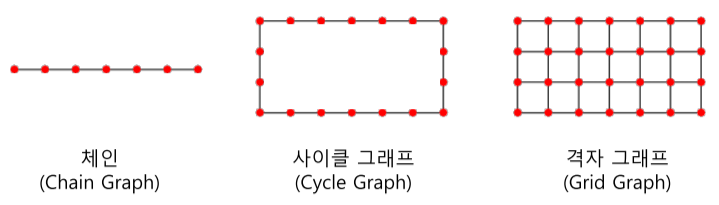
[img. 작지 않은 세상들]
연결성의 두터운-꼬리 분포
정점의 연결성(Degree)은 그 정점과 연결된 간선의 수, 해당 정점의 이웃들의 수를 의미
-
$d(v),\ d_v,\ N(v) $로 표기함.
| 연결성 | 그래프 |
|---|---|
| $d(1)=2\d(2)=3\d(3)=2\d(4)=3\d(5)=3\d(6)=1$ | 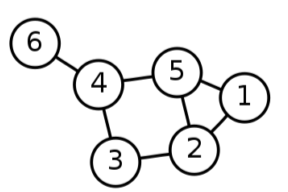 |
[fig. 연결성(이웃)의 예시]
- 정점의 나가는 연결성(Out Degree)은 그 정점에서 나가는 간선의 수를 의미
-
$d_{out}(v), N_{out}(v) $로 표시
-
- 정점의 들어오는 연결성(In Degree)은 그 정점에서 들어오는 간선의 수를 의미.
-
$d_{in}(v), N_{in}(v) $로 표시
-
| 연결성 | 그래프 |
|---|---|
| $d_{in}(1)=1,\ d_{out}(1)=1\d_{in}(2)=3,\ d_{out}(1)=1\d_{in}(3)=0,\ d_{out}(3)=2\d_{in}(4)=1,\ d_{out}(4)=2\d_{in}(5)=2,\ d_{out}(5)=2\d_{in}(6)=1,\ d_{out}(6)=0\$ | 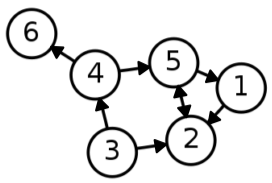 |
[fig. 방향 그래프의 연결성(이웃)의 예시]
실제 그래프의 연결성 분포는 두터운 꼬리(Heavy Tail)를 가짐 (ex)BTS와 강사님의 트위터 팔로워 수)
- 이는 연결성이 매우 높은 허브(Hub) 정점이 존재함을 의미.
반면에 랜덤 그래프의 연결성 분포는 정규분포와 유사함(ex) 인간의 키 분포).
- 허브 정점이 존재할 확률이 아주 적음.
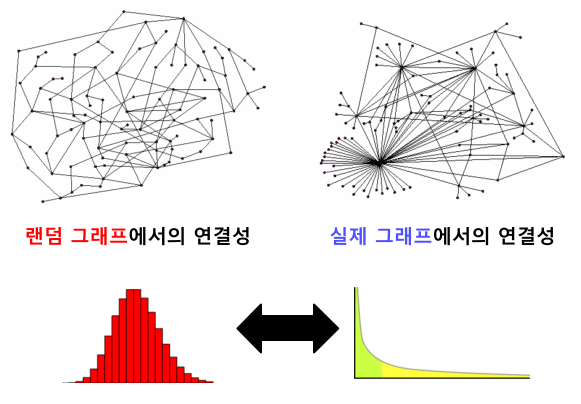
[img. 랜덤 그래프와 실제 그래프의 차이]
거대 연결 요소
연결 요소(Connected Component)는 다음 조건들을 만족하는 정점들의 집합을 의미합니다.
- 연결 요소에 속하는 정점들은 경로로 연결될 수 있습니다.
- 1.의 조건을 만족하면서 정점을 추가할 수 없습니다.
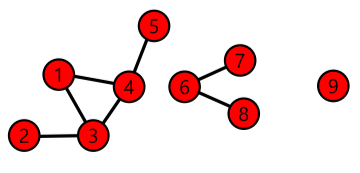
[img. {1,2,3,4,5}, {6,7,8}, {9} 총 3개의 연결 요소가 있다.]
실제 그래프에는 거대 연결요소(Giant Connected Component)가 존재하며, 대다수의 정점을 포함함.
랜덤 그래프에도 높은 확률로 거대 연결요소가 존재함.
- 단, Random Graph Theory에 의해 정점들의 평균 연결성이 1보다 충분히 커야함.
| 실제 그래프 | 랜덤 그래프 |
|---|---|
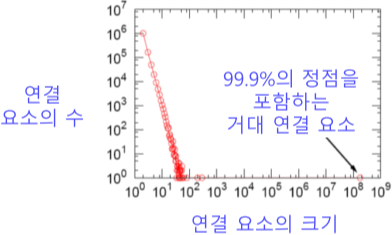 |
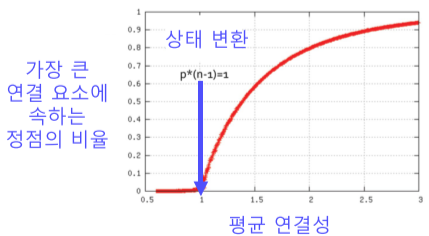 |
[fig. 실제 그래프 vs 랜덤 그래프에서의 거대 연결 요소]
군집 구조
군집(Community)이란 다음과 같은 조건을 만족하는 정점들의 집합.
- 집합에 속하는 정점 사이에는 많은 간선이 존재함
- 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재
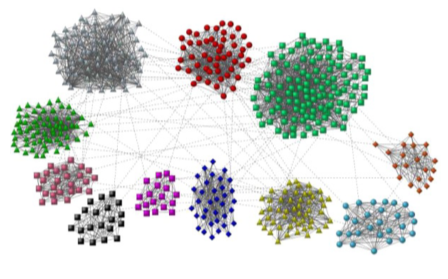
[img. 군집 그래프]
지역적 군집 계수(Local Clustering Coefficient)는 한 정점에서 군집의 형성 정도를 측정 가능
- 정점 $i$의 지역적 군집 계수($C_i$)는 정점 $i$의 이웃들의 쌍 중 간선으로 직접 연결된 것의 비율을 의미
- 연결성(이웃)이 0인 정점에서는 지역적 군집 계수 정의가 안됨.
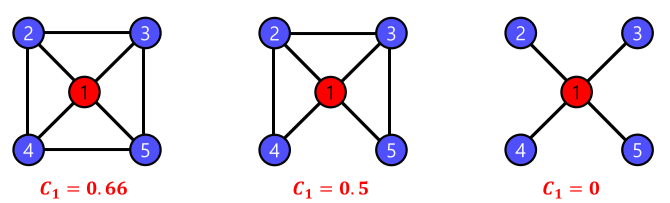
[img. 지역적 군집 계수의 예시]
전역 군집 계수(Global Clustering Coefficient)는 전체 그래프에서 군집의 형성 정도를 측정
- 그래프 G의 전역 군집 계수는 각 정점에서의 지역적 군집 계수의 평균
- 단, 지역적 군집 계수가 정의되지 않는 정점은 제외
실제 그래프에서 군집 계수가 높은(=군집이 많은) 이유
- 동질성(Homophily) : 서로 유사한 정점끼리 간선으로 연결될 가능성이 높음
- 같은 인종간 관계 그래프
- 전이성(Transitivity) : 공통 이웃은 간선 연결이 생길 확률이 높음
- 친구에게 친구를 소개
반면 랜덤 그래프는 간선 연결 확률이 독립적(Independent)이므로 지역적, 전역 군집 계수가 높지 않음.
군집 계수 및 지름 분석
Lab의 [Graph-2]Graph_Property.ipynb 참조
| 균일 그래프(Regular Graph) | 작은 세상 그래프(Small-world Graph) | 랜덤 그래프(Random Graph) | |
|---|---|---|---|
| 군집 계수 | 큼 | 큼 | 작음 |
| 지름 | 큼 | 작음 | 큼 |
페이지 랭크 알고리즘
페이지 랭크의 배경
웹은 웹페이지와 하이퍼링크로 구성된 거대한 방향성 있는 그래프.
- 웹페이지 : 정점 + 키워드 정보
- 하이퍼링크: 간선
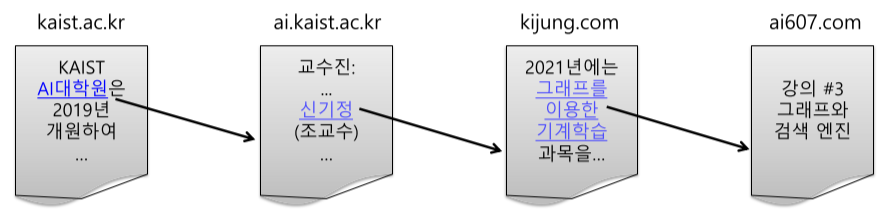
[img. 웹은 그래프이다.]
검색엔진의 발전
- 웹을 거대한 디렉토리로 정리
- 웹페이지의 수가 증가하며 카테고리의 수와 깊이가 무한정 커짐
- 카테고리 구분이 모호하고 저장과 검색이 어려움
- 웹페이지에 포함된 케워드에 의존한 검색엔진
- 사용자가 입력한 키워드에 대해 키워드를 여럿 포함한 웹페이지를 반환
- 악의적인 웹페이지에 취약하다는 단점(축구라는 단어가 여러번 포함된 성인 사이트)
사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾기 위해 PageRank 알고리즘을 활용함.
- 래리 페이지와 세르게이 브린이 발표
페이지랭크의 정의
하이퍼링크를 통한 웹페이지의 투표를 통해 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾을 수 있음
- 웹페이지 u가 v를 하이퍼링크로 연결(투표)한다면, v는 관련성이 높고 신뢰하고 있다는 것을 의미.(논문과 비슷)
- 즉, 들어오는 간선이 많을 수록 신뢰할 수 있다.
- 단, 악의적인 인용 등이 있으며 이를 막기위해 가중 투표를 도입
가중 투표: 관련성이 높고 신뢰할 수 있는 웹사이트의 투표에 더 높은 점수를 주는것
- 그러한 웹사이트가 높은 관련성과 신뢰성을 얻으려면, 투표를 많이 받아야함. => 재귀 구조
이러한 웹페이지의 관련성 및 신뢰도를 페이지랭크 점수라고 함.
- 웹페이지는 각각의 나가는 이웃에게 $\frac{자신의\ 페이지랭크\ 점수}{나가는\ 이웃의\ 수}$만큼의 가중치로 투표를 함
- 웹페이지의 페이지랭크 점수는 받은 투표의 가중치 합으로 정의됨.
[math. 페이지랭크 점수의 정의]
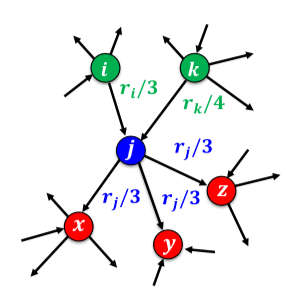
[img. $r_j$가 웹페이지 j의 페이지랭크의 점수일 때, 예시]
-
위 그림에서 웹페이지 j의 투표시 가중치는 $r_j$/3
-
웹페이지 j의 페이지랭크 점수 $r_j=r_i/3+r_k/4$
| 정점 별 페이지랭크 | 웹페이지 그래프 |
|---|---|
| $r_y=r_y/2+r_a/2\r_a=r_y/2+r_m\r_m=r_a/2$ | 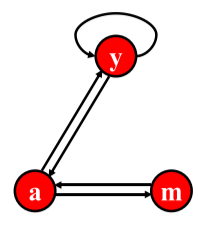 |
[fig. 웹페이지 별 페이지랭크 점수 연립 방정식]
페이지 랭크는 임의 보행(Random Walk)의 관점에서도 정의 가능.
-
웹서퍼가 t번째 방문한 웹페이지가 웹페이지 i일 확률을 $p_i(t)$
-
웹서퍼가 무한히 방문해 t가 무한히 커지면, 다음이 성립
[math. 임의 보행 관점에서의 페이지랭크]
\[r_j=\sum_{i\in N_{in}(j)}\frac{r_i}{d_{out}(i)}: 투표\ 관점에서\ 정의한\ 페이지랭크\ 점수\ r\\ p_j=\sum_{i\in N_{in}(j)}\frac{p_i}{d_{out}(i)}:임의\ 보행\ 관점에서\ 정의한\ 정상\ 분포\ p\][math. 투표 관점의 페이지 랭크 점수 == 임의 보행 관점에서의 정상 분포]
페이지랭크의 계산
반복곱(Power Iteration)을 이용해 페이지 랭크 점수 가능
- 각 웹페이지 i의 페이지랭크 점수 $r_i^{(0)}$를 동일하게 $\frac{1}{웹페이지의\ 수}$로 초기화
- 아래 식을 이용하여 각 웹페이지의 페이지랭크 점수를 갱신
[math. 페이지랭크 점수 갱신 식]
- 페이지랭크 점수가 수렴($r^t와\ r^{t+1}이\ 유사해질때\ 까지$)하였으면 종료, 아닌 경우 2로 회귀
graph LR
y((y))-->a
y-->y
a((a))-->y
a-->m
m((m))-->a
| 반복 | 0 | 1 | 2 | 3 | | 수렴 |
| :—: | —- | —- | —- | —– | —- | —- |
| $r_y$ | 1/3 | 1/3 | 5/12 | 9/24 | | 6/15 |
| $r_a$ | 1/3 | 3/6 | 1/3 | 11/24 | … | 6/15 |
| $r_m$ | 1/3 | 1/6 | 3/12 | 1/6 | | 3/15 |
[fig. 페이지랭크 점수 갱신의 예시]
단, 언제나 수렴하지 않을 수도 있으며, 합리적인 점수로 수렴하는 것도 보장하지 않는다.
- 수렴하지 않는 예시
graph LR
a((a))-->b
subgraph 스파이더트랩
b((b))--->c((c))--->b
end
스파이더 트랩(Spider Trap) : 들어오는 간선은 있지만 나가는 간선은 없는 정점 집합
| 반복 | 0 | 1 | 2 | 3 | 수렴 | |
|---|---|---|---|---|---|---|
| $r_a$ | 1/3 | 0 | 0 | 0 | X | |
| $r_b$ | 1/3 | 2/3 | 1/3 | 2/3 | … | X |
| $r_c$ | 1/3 | 1/3 | 2/3 | 1/3 | X |
[fig. 수렴하지 않는 스파이더 트랩의 예시]
- 반복 1, 2, 1, 2,가 무한히 반복
- 합리적인 점수로 수렴하지 않는 예시(0으로 수렴함)
graph LR
a((a))-->b
subgraph 막다른 정점
b((b))
end
들어오는 간선은 있지만 나가는 간선은 없는 막다른 정점(Dead End) 문제
| 반복 | 0 | 1 | 2 | 3 | | 수렴 |
| :—: | —- | —- | —- | —- | —- | —- |
| $r_a$ | 1/2 | 0 | 0 | 0 | | 0 |
| $r_b$ | 1/2 | 1/2 | 0 | 0 | … | 0 |
[fig. 막다른 정점의 예시]
- 전부 0으로 수렴
위와 같은 문제를 해결하기 위해 순간이동(Teleport) 도입
수정된 웹서퍼의 순간이동 행동
- 현재 웹페이지에 하이퍼링크가 없으면, 전체 웹페이지 중, 균일 확률로 임의의 웹페이지로 순간이동
- 현재 웹페이지에 하이퍼링크가 있다면, 앞면이 나올 확률이 $\alpha$인 동전을 던집니다.
- $\alpha : 감폭 비율 (Dampling\ Factor)$, 보통 0.8 정도임.
- 앞면이라면, 하이퍼링크 중 하나를 균일한 확률로 선택해 클릭 (이전 웹서퍼와 동일)
- 뒷면이라면, 전체 웹페이지 중, 균일 확률로 임의의 웹페이지로 순간이동
순간이동의 도입으로 인해 페이지 랭크 점수 계산은 다음과 같이 변한다.
- 각 막다른 정점에서 (자신을 포함) 모든 다른 정점으로 가는 간선을 추가
- 아래 수식을 사용하여 반복곱을 수행
\(r_j=\left(\sum_{i\in N_{in}(j)}\left( \alpha\frac{r_i}{d_{out}(i)}\right)\right)_{가}+\left((1-\alpha)\frac{1}{|V|}\right)_나\\|V|: 전체\ 웹페이지의\ 수\\
식\ 가:하이퍼링크를\ 따라\ 정점\ j에\ 도착할\ 확률\\식\ 나: 순간이동을\ 통해\ 정점\ j에\ 도착할\ 확률\)
[math. 순간이동에 의한 새로운 페이지랭크 점수 계산식]
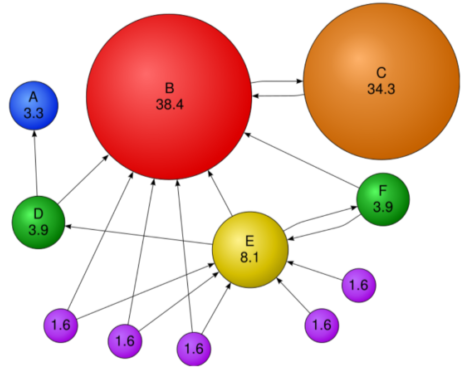
[img. 수정된 페이지랭크 점수 예시]
- C는 1표만 받지만 B의 귀중한 한표라서 점수가 큼
- 1.6 보라색 들은 들어오는 간선이 없지만 Teleport에 의해서 점수 획득
페이지 랭크 실습
Lab의 [Graph-3]PageRank.ipynb 참조
그래프를 이용한 바이럴 마케팅
그래프를 통한 전파의 예시
- SNS를 이용한 마케팅, 정보, 단체 행동 등이 전파됨.
- 컴퓨터 네트워크 장비의 고장, 파워 그리드의 정전 전파
- 사회에서의 질병 전파
이러한 전파 과정을 체계적으로 이해하고 대처하기 위해서 수학적 모형화가 필요함.
- 의사 결정 기반 전파 모형
- 확률적 전파 모형
의사 결정 기반 전파 모형
주변 정점(사람)들의 의사결정을 고려하여 각자 의사결정을 내리는 경우에 사용하는 모형
- 각 국가별 주요 사용 SNS, 비디오 테이프 표준화 등이 있음
간단한 형태의 의사결정 기반의 전파 모형으로, 선형 임계치 모형(Linear Threshold Model)이 있음
| 사용 기술 | A | B | A,B |
|---|---|---|---|
| 도식 | 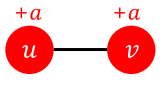 |
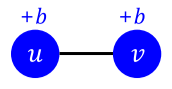 |
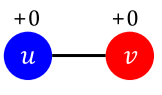 |
| 증가하는 행복 | +2a | +2b | 0 |
[fig. u, v 두 사람이 A, B라는 호환되지 않는 기술을 사용시 얻는 행복]
- 위 두 사람은 행복이 증가하지 않는 0보다, +2a, +2b를 비교하여 더 이득이 되는 방향으로 바꿀 것이다.
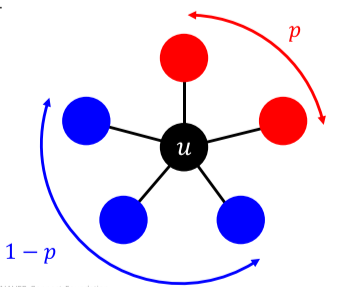
[fig. 임계치 q를 구하기 위한 모형]
p 비율의 u의 이웃이 A를 , 1-p 비율의 u의 이웃이 B를 선택했을 때,
- A를 골랐을 때의 u의 행복이 ap, B를 골랐을 때의 u의 행복이 b(1-p)라고 할 때
- u는 ap > b(1-p)일 때, A를, ap < b(1-p)일 때, B를 고를 것이다.
- 이 식을 바꾸어 $p > \frac{b}{a+b}$일 때 A를 고르며 이를 임계치 q$(=\frac{b}{a+b})$라고 한다.
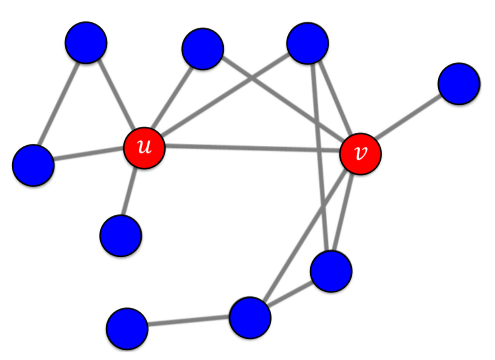
[img. u와 v가 처음으로 A 기술를 사용한 얼리어 답터(시드집합)일 때의 상황]
만약 A기술과 B 기술의 행복 a, b가 같고, u와 v가 해당 기술을 처음 사용한 얼리어답터(시드집합, Seed Set)이라고 가정하면, 해당 모형의 경과는 다음과 같다.
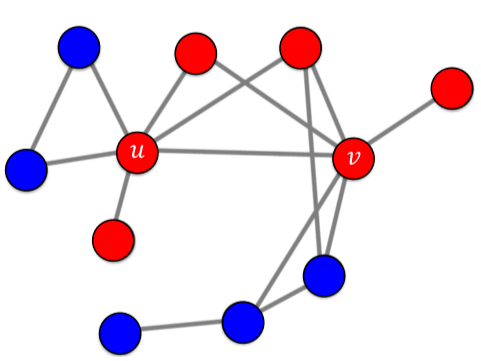
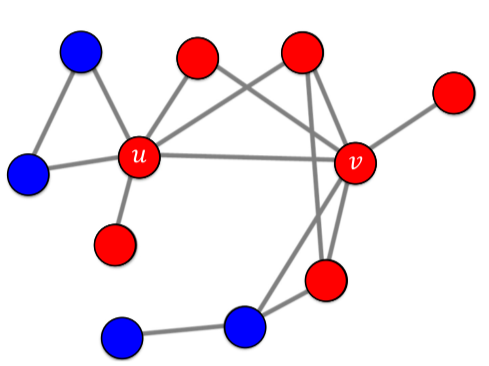
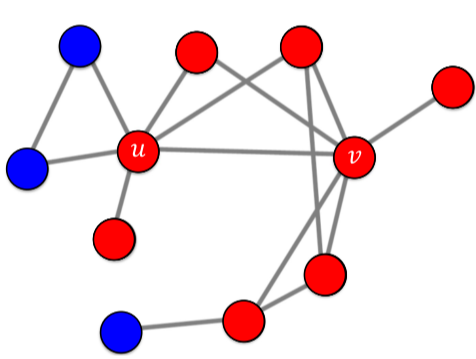
| 1 | 2 | 3 | 4 |
|---|---|---|---|
 |
 |
 |
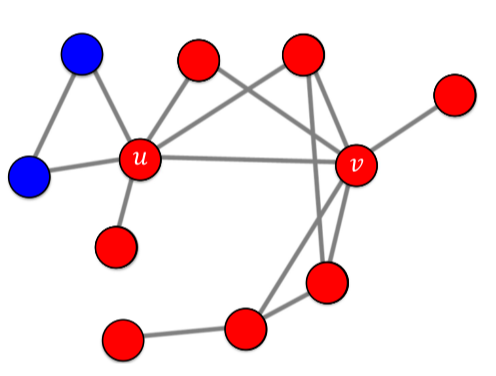 |
[fig. A기술의 선형 임계치 모형 전파, 4번 이후로 더이상 전파는 없다.]
- 4번 이후로 2개의 파란 정점은 A기술을 사용하는 간선이 u 하나 뿐이며, 이는 33%으로 50%를 넘기지 못하므로 전파되지 않는다.
확률적 전파 모형
질병, 정전 등의 모형에서는 위의 의사결정 기반 모형이 어울리지 않다.
- 누구도 질병에 걸리도록 의사결정을 내리는 사람은 없기 때문이다.
질병에 걸리는 것은 확률적 과정이므로 확률적 전파 모형을 고려해야 한다.
그 예시로 독립 전파 모형(Independent Cascade Model)이 있다.
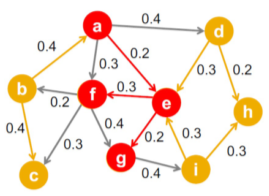
[img. 독립 전파 모형은 보통 방향성이 있고 가중치가 있는 그래프를 가정한다.]
간선 (u, v)의 가중치 $p_{uv}$는 u가 감염자, 이웃 v가 감염자가 아닐 때, u가 이웃 v를 감염시킬 확률을 의미한다.
이때 서로 다른 이웃이 전염될 확률은 독립적이다.
- 예를 들어, u가 감염되었을 때 u가 v를 감염시킬 확률은 u가 w를 가염시킬 확률과 독립적이다.
이전 모형과 마찬가지로 첫 감염자들을 시드 집합(Seed Set)이라고 부르며, 더이상 새로운 감염자가 없을 때까지 감염시킨다.
감염자의 회복을 가정하는 SIS, SIR 등의 다른 전파 모형도 있음
바이럴 마케팅과 전파 최대화 문제
바이럴 마케팅은 소비자들로 하여금 상품에 대한 긍정적인 입소문을 내게 하는 기법이다.
소문의 시작점(시드 집합, Seed Set)이 중요하며, 누굴 고르냐에 따라 전파되는 범위가 크게 영향을 받는다.
- 소셜 인플루언서(Social Influencer)들이 높은 광고비를 받는 이유
- 영국 윌리엄 왕자 부인 케이트 미들턴의 이름을 딴 미들턴 효과 라는 용어도 있음
| 시드 집합의 선택에 따른 전파 크기 비교 |
|---|
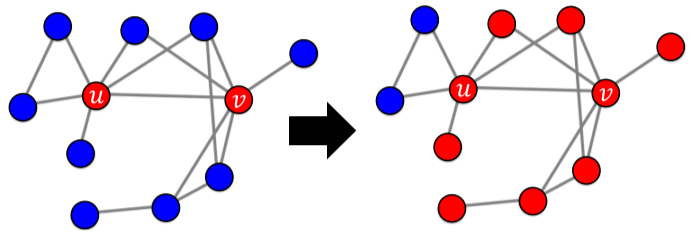 |
| 2 정점을 제외하고 모두 전파 |
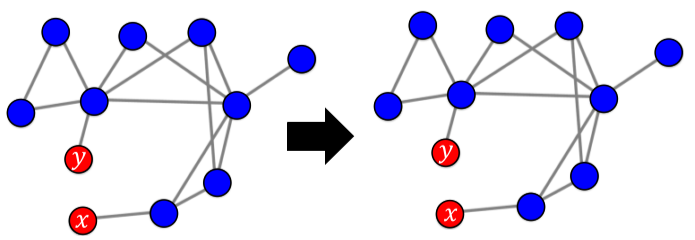 |
| 첫 2명을 제외하고 전파되지 않았음. |
[img. 이전 선형 임계치 모형의 시드집합 선택에 따른 결과 비교]
이러한 이유로 그래프, 전파 모형 그리고 시드 집합의 크기가 주어졌을 대 전파를 최대화하는 시드 집합을 찾는 문제를 전파 최대화(Influence Maximization) 문제라고 부름.
- 하지만 최고 효율의 시드 집합을 찾는 이 문제는 아주 어려운 문제이다.
-
V 개의 정점의 그래프에서 시드 집합의 크기를 k개로 제한하여도 경우의 수가 $(\frac{ V }{k})$개이다. - 사람이 10000명, 찾을 인플루언서가 10명이어도 약 $2.75\times 10^{33}$개 정도의 수
- 이론적으로 NP-hard 문제임이 증명됨
- NP-난해(NP-hard) : 적어도 NP(푸는 시간이 $O(n)$ 이상 드는 문제) 문제 이상은 어려운 문제를 의미
너무나도 어려운 문제이므로 최고의 시드 집합을 찾는 것은 불가능하며, 휴리스틱 위주로 정답에 가까운 시드 집합을 찾아야한다.
- 휴리스틱으로 찾은 답은 최적의 답임이 보장되지 않는다.
-
휴리스틱 방법 - 정점의 중심성(Node Centrality)
- 시드 집합의 크기가 k개로 고정되어 있을시, 정점의 중심성이 높은 순으로 k개 정점을 선택
- 페이지랭크 점수, 연결 중심성, 근접 중심성, 매개 중심성 등이 있음
-
탐욕 알고리즘(Greedy Algorithm)
-
시드 집합의 원소, 즉 최초 전파자를 한번에 한 명씩 선택하는 방법
-
최초 전파자 간의 조합의 효과를 고려하지 않고, 근시안적으로 최초 전파자를 선택하는 과정을 반복함.
-
즉, 정점의 집합을 {1,2, …, V }라고 할 때 1) 집합 {1},{2},…,{ V }를 비교하여, 전파를 최대화하는 시드 집합을 찾는다. - 이때, 전파의 크기 비교 방법은 시뮬레이션을 반복하여 생긴 평균 값을 사용함.
2) 집합 {x}가 뽑히면, 집합 {x, 1}, {x, 2}, …, {x, V }를 비교하여 전파를 최대화 하는 시드 집합을 찾음. 3) 집합 {x, y}가 뽑히면 또 집합 {x, y, 1}, {x, y, 2}, …, {x, y, V }를 비교하여 전파 최대화 집합을 찾음 4) 위 과정을 목표하는 크기의 시드 집합에 도달할 때까지 반복
- 독립 전파 모형일 시, 이론적으로 최저 성능 정확도가 보장됨(보장 됬으므로 휴리스틱은 아님)
\(r_{greedy}\geq (1-\frac{1}{e}) * r_{optimal} \\ where\ (1-\frac{1}{e})\approx0.632\\ r_{greedy}:\ 탐욕\ 알고리즘으로\ 찾은\ 시드\ 집합의\ 의한\ 전파의\ (평균)크기\\ r_{optimal}:\ 이론상\ 최고의\ 시드\ 집합에\ 의한\ 전파의\ (평균)크기\)
[math. 탐욕 알고리즘의 최저 성능]
-
전파 모형 시뮬레이터 구현
Lab의 [Graph-4]Influence_Model.ipynb 참조
그래프 군집 구조
군집 구조와 군집 탐색 문제
군집(Community)의 정의 : “기계학습을 이용한 그래프 학습에서 군집 구조” 참조
온라인 소셜 네트워크의 군집들은 사회적 무리(Social Circle)을 의미하는 경우가 많음
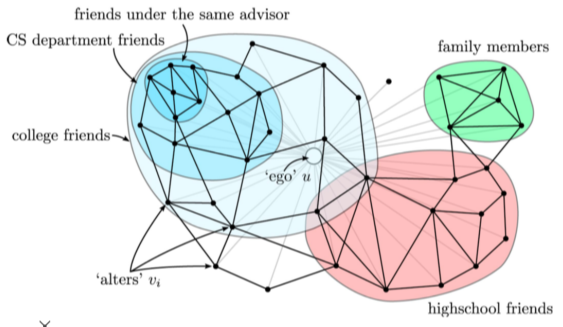
[img. SNS에서의 사회적 군집]
군집을 분석하여 조직내 부정 행위 군집, 분란을 탐색하거나, 키워드 군집 등을 확인할 수 있다.
그래프 내부에 군집들을 적절하게 나누는 문제를 군집 탐색(Community Detection) 문제라고 하며, 각 정점이 한 개의 군집에 속하도록 나누며, 비지도 기계학습 문제인 클러스터링(Clustering)과 상당히 유사함.
- 클러스터링 : feature들의 벡터 인스턴스를 그룹으로 묶음
- 군집 탐색: 군집의 정점들을 그룹으로 묶음
군집 구조의 통계적 유의성과 군집성
배치 모형(Configuration Model)은 각 정점의 연결성(Degree, 이웃의 수)을 보존한 상태에서 간선들을 무작위로 재배치하여 얻은 그래프이다.
- 임의의 두 정점 사이에 간선이 존재할 확률은 두 정점의 연결성에 비례
- 아래 예시 이웃들은 각 1, 3, 2 ,2 이며, 이웃의 수가 1, 3, 2, 2 로만 같게 연결하면 됨(누구와 연결되는 지는 관계 없음)
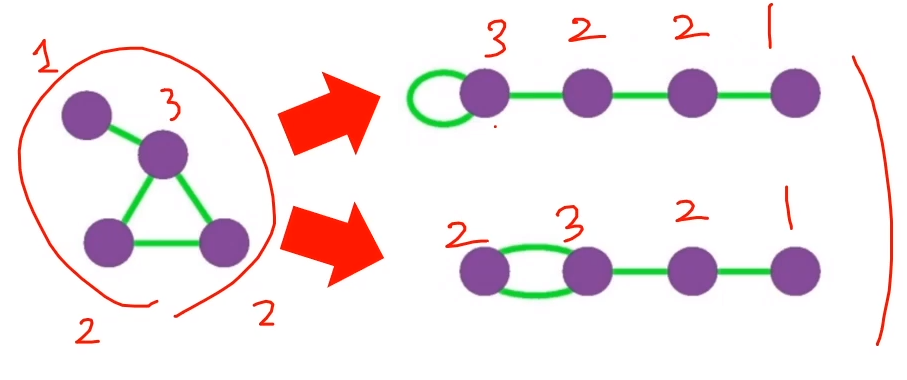
[img. 배치모형의 형성]
군집성(Modularity): 군집 구조의 통계적 유의성
- 이를 이용해 군집 탐색의 성공 여부를 판단할 수 있으며 다음과 같이 계산됨.
\(\frac{1}{2|E|}\sum_{s\in S}(그래프에서\ 군집\ s\ 내부\ 간선\ 수 - 배치\ 모형에서\ 군집\ s\ 내부\ 간선\ 수의\ 기대값)\)
[math. 군집성의 계산]
- -1 ~ +1 사이의 값을 가지며, 0.3~0.7 정도의 값을 가질 때 통계적으로 유의미한 군집임.
- 그래프와 군집들의 집합 S가 주어졌을 때, 각 군집 $s \in S$가 군집의 성질을 잘 만족하는 지 알아보기 위해, 군집 내부의 간선의 수를 그래프와 배치 모형에서 비교.
- 다만 배치 모형은 무작위로 형성되므로 기대값을 비교
- 즉, 무작위로 연결된 배치 모형과 비교하여 통계적 유의성을 판단함.
- 배치모형 대비 그래프에서 군집 내부 간선의 수가 월등히 많을 수록 성공한 군집 탐색.
군집 탐색 알고리즘
- Girvan-Newman(걸반-뉴먼) 알고리즘
전체 그래프에서 시작해서 점점 작은 단위를 검색하는 하향식(Top-Down) 군집 탐색 알고리즘
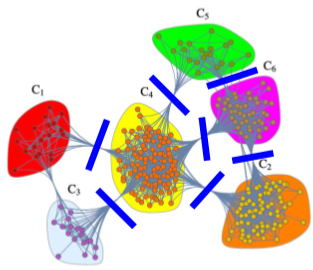
[img. Girva-Newman 알고리즘]
1) 전체 그래프에서 시작
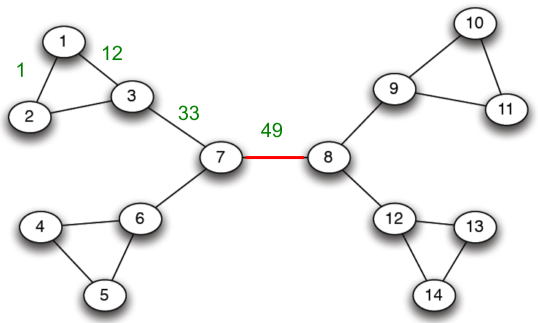
2) 매개 중심성이 높은 순서로 간선을 제거하면서, 군집성을 변화를 기록
- 매개 중심성(Betweenness Centrality) 간선 : 다른 군집을 연결하는 다리(Bridge) 역할의 간선
- 매개 중심성 : 정점 간의 최단 경로에 놓이는 횟수
[math. 매개 중심성의 계산]
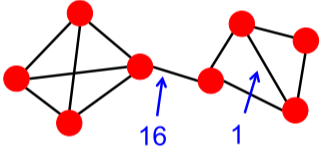
[img. 매개 중심성의 예시, 16이 다리 역할을 한다.]
3) 간선 제거 때마다 재계산하여 매개 중심성 갱신, 군집성을 기록하고, 간선이 모두 제거될 때 까지 반복.
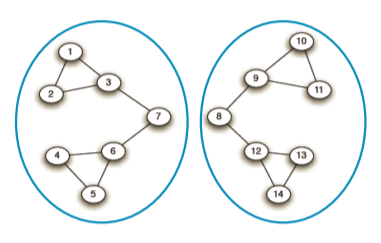
| 1 | 2 | 3 | 4 |
|---|---|---|---|
 |
 |
 |
 |
[math. 간선의 제거, 제거 정도 따라 다른 입도(Granularity)의 군집 구조가 나타남 ]
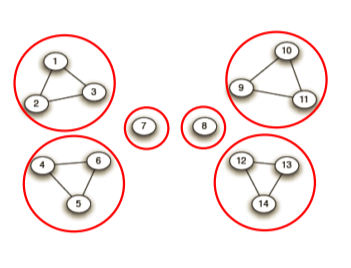
4) 군집성이 가장 커지는 상황을 복원
- 기록한 군집성을 비교하여 군집성이 최대가 되는 지점으로 복원
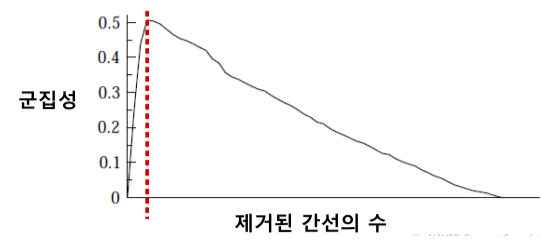
[img. 군집성이 최대가 되는 시점]
5) 이때, 서로 연결된 정점들, 즉 연결 요소를 하나의 군집으로 간주
- Louvain 알고리즘
개별 정점에서 시작해 큰 군집을 형성하는 대표적인 상향식(Bottom-Up) 군집 탐색 알고리즘
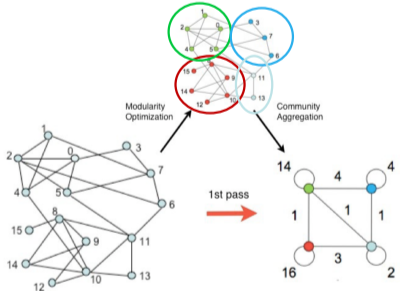
[img. Luvain 알고리즘]
1) Louvain 알고리즘은 개별 정점으로 구성된 크기 1의 군집들로부터 시작
2) 각 정점 u를 기존 혹은 새로운 군집으로 이동하며, 이 때, 군집성이 최대화되도록 군집을 결정
3) 더 이상 군집성이 증가하지 않을 때까지 2)를 반복
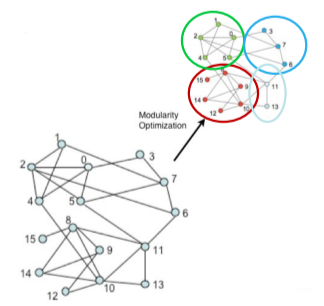
[img. 첫 시작시 각 정점을 군집으로 친다.]
4) 각 군집을 하나의 정점으로 하는 군집 레벨의 그래프를 얻은 뒤 3) 을 수행
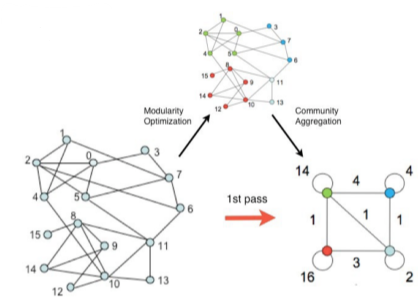
[img. 각 군집을 하나의 정점으로 바꿈]
5) 한 개의 정점이 남을 때까지 4)를 반복
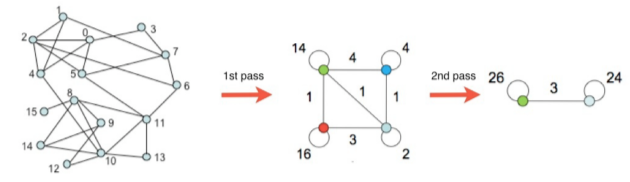
[img. 군집의 수가 줄다가 최종적으로는 군집이 하나만 남게 된다.]
중첩이 있는 군집 탐색
실제 그래프의 군집들은 중첩되어 있는경우가 많다.
중첩 군집 탐색은 주어진 그래프의 확률을 최대화하는 중청 군집 모형을 찾는 과정이다.
- 최우도 추정치(Maximum Likelihood Estimate)를 찾는 과정이라고도 한다.
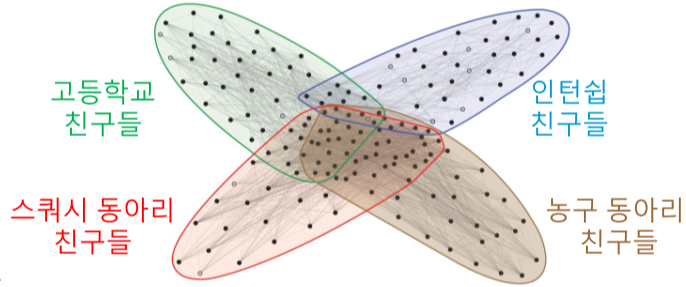
[img. 실제 사회에서의 중첩 군집]
중첩 군집 모형의 가정
-
각 정점은 여러 개의 군집에 속할 수 있음
-
각 군집 A에 대하여, 같은 군집에 속하는 두 정점은 $P_A$확률로 간선으로 직접 연결됨
-
두 정점이 여러 군집에 동시에 속할 경우 간선 연결 확률은 독립적임
-
두 정점이 군집 A와 B에 동시에 속할 경우, 두 정점이 간선으로 직접 연결될 확률은
1-(1-$P_A$)(1-$P_B$).
-
-
어느 군집에도 함께 속하지 않는 두 정점은 낮은 확률 $\epsilon$으로 직접 연결됨.
위의 중첩 군집 모형으로 주어진 그래프의 확률을 다음과 같이 계산할 수 있다.
그래프의 확률
=
그래프의 각 간선의 두 정점이 (모형에 의해) 직접 연결될 확률
X
그래프에서 직접 연결되지 않은 각 정점 쌍이 (모형에 의해) 직접 연결되지 않을 확률
[code. 그래프 확률 계산식]
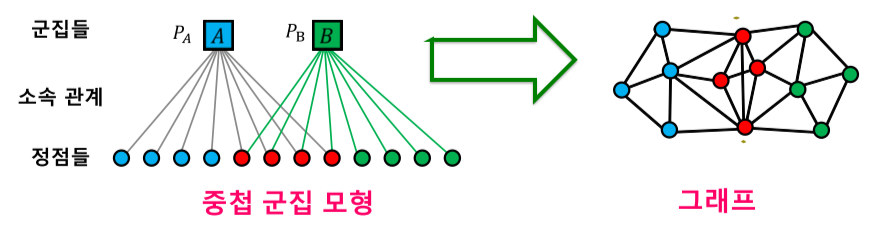
[img. 그래프 확률 계산]
중첩 군집 탐색을 용이하게 하기위해 완화된 중첩 군집 모형을 사용할 수 있다.
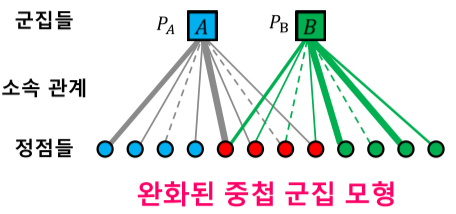
[img. 완화된 중첩 군집 모형의 느슨한 소속감]
군집에 속하거나 속하지 않거나, 둘 뿐만아니라 그 중간 상태를 표시하기 위해 정점이 각 군집에 속해 있는 정도를 실숫값으로 표현 가능
실숫값으로 표현되므로 경사하강법 등의 최적화 도구로 모형을 탐색할 수 있다.
Girvan-Newman 알고리즘 구현 및 적용
[Graph-5]Girvan-Newman_Algorithm_Real_World_Graph_Community_Detection.ipynb
추천 시스템
우리 주변의 추천 시스템
아마존, 넷플릭스, 유튜브, 페이스북 등에서 추천 시스템을 이용한다.
추천 시스템은 사용자 각각이 구매할 만한 혹은 선호할 만한 상품을 예측하거나 선호를 추정함.
- 즉 미래의 간선을 예측하는 문제 또는,
- 누락된 간선의 가중치를 추정하는 문제
로 해석 가능하다.
사용자 구매 기록을 그래프로 표현 가능하며,
- 구매 기록 같은 암시적(Implicit) 선호와
- 평점같은 명시적(Explicit) 선호가 존재한다.

[img. 추천 시스템의 문제에 대한 해석]
내용 기반 추천 시스템
각 사용자가 구매/만족했던 상품과 유사한 것을 추천하는 방법
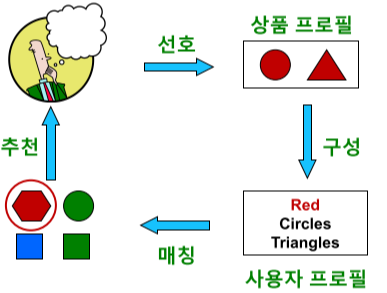
[img. 내용 기반 추천의 4단계]
-
상품 프로필(Item Profile) 수집 단계
- 상품 프로필 : 해당 상품의 특성을 나열한 벡터
- ex) 영화 : [로맨스, 코미디, 액션, 공포] = [0,1,0,0] => 원-핫 인코딩 형태
-
사용자 프로필(User Profile) 구성 단계
- 사용자 프로필 : 선호한 상품의 상품 프로필을 선호도를 사용하여 가중 평균하여 계산한 벡터
- ex) 여러 영화 프로필의 가중 평균 : [로맨스, 코미디, 액션, 공포] = [0.1,0.9,0.2,0.3] => 원-핫 인코딩 형태
-
사용자 프로필과 다른 상품들의 상품 프로필을 매칭하는 단계
-
사용자 프로필 벡터 $\vec u$와 상품 프로필 벡터 $\vec v$ 일 때, 코사인 유사도를 계산
\(코사인\ 유사도 = \frac{\vec u \cdot \vec v}{\left\|\vec u\right\|\left\|\vec v\right\|}\)
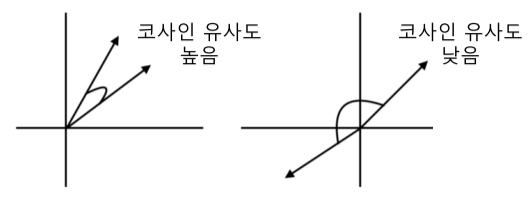
[img. 코사인 유사도 계산]
-
즉, 두 벡터 사이각의 코사인 값을 계산
-
코사인 유사도가 높을 수록, 해당 사용자가 과거 선호했던 상품들과 해당 상품이 유사함
-
-
사용자에게 상품을 추천하는 단계
- 코사인 유사도가 높은 상품들을 추천
| 장점 | 단점 |
|---|---|
| 1. 다른 사용자의 구매 기록이 필요하지 않음 2. 독특한 취향의 사용자에게도 추천이 가능 3. 새 상품에 대해서도 추천이 가능 4. 추천의 이유를 제공할 수 있음 - 예시 : 로멘스영화를 많이 보니 로맨스 영화 추천했음 |
1. 상품에 대한 부가 정보가 없는 경우에는 사용 불가능 2. 구매 기록이 없는 사용자에게 사용 불가능 3. 과적합(Overfitting)으로 지나치게 협소한 추천 가능성 |
[fig. 내용 기반 추천 시스템의 장단점]
협업 필터링
유사한 취향의 사용자들을 이용해 추천하는 방법
- 사용자와 유사한 취향의 사용자들을 찾기
- 유사한 취향의 사용자들이 선호한 상품 찾기
- 선호한 상품을 사용자에게 추천
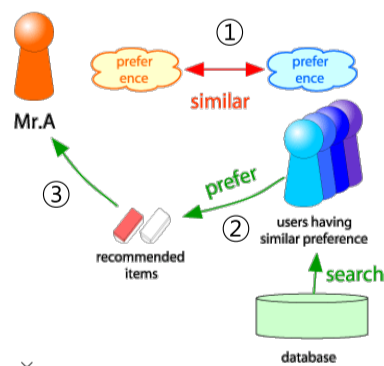
[img. 협업 필터링의 3단계]
취향의 유사성은 상관계수(Correlation Coefficient)를 통해 측정
\(sim(x,y)=\frac{\sum_{s\in S_{xy}}(r_{xs}-\bar{r}_x)(r_{ys}-\bar{r}_y)}{\sqrt{\sum_{s\in S_{xy}}(r_{xs}-\bar{r}_x)^2}\sqrt{\sum_{s\in S_{xy}}(r_{ys}-\bar{r}_y)^2}}\\
r_{xs}:사용자\ x의\ 상품\ s에\ 대한\ 평점\\
\bar{r_x}:사용자\ x가\ 매긴\ 평균\ 평점\\
S_{xy}:사용자\ x와\ y가\ 공동\ 구매한\ 상품들\)
[math. 상관계수 식]
- 통계에서 나온 개념임
| 반지의제왕 | 겨울왕국 | 라푼젤 | 해리포터 | 미녀와 야수 | |
|---|---|---|---|---|---|
지수 |
4 |
1 |
2 |
5 |
? |
제니 |
5 |
1 |
? |
4 |
2 |
| 로제 | 2 | 5 | 5 | ? | 4 |
[fig. 취향 유사도 계산]
지수와 로제의 취향 유사도는 다음과 같다.
\(0.88=\frac{(4-3)(5-3)+(1-3)(1-3)+(5-3)(4-3)}{\sqrt{(4-3)^2+(1-3)^2+(5-3)^2}\sqrt{(5-3)^2+(1-3)^2+(4-3)^2}}\\\)
둘의 취향은 상당히 비슷함
이런 식으로 비슷한 사람들을 모아 위에서 구한 취향의 유사도를 가중치로 사용한 평점의 가중 평균을 통해 평점을 추정
\(평점\ \hat{r}_{XS}=\frac{\sum_{y\in N(x;s)}sim(x,y)\cdot r_{ys}}{\sum_{y\in N(x;s)}sim(x,y)}\\
N(x;s): 상품\ s를\ 구매한\ 사용자\ 중에\ x와\ 취향이\ 가장\ 유사한\ k명의\ 사용자들\)
[math. 평점의 추정]
마지막으로 사용자가 구매하지 않은 상품들의 추정한 평점 중에서 가장 평점이 높은 상품을 추천.
| 장점 | 단점 |
|---|---|
| 상품에 대한 부가 정보가 없는 경우에도 사용 가능 | 1. 충분한 수의 평점 데이터가 누적되어야 효과적 2. 새 상품, 새로운 사용자에 대한 추천 불가능 3. 독특한 취향의 사용자(비슷한 사람 적음)에게 추천 힘듬 |
[fig. 협업 필터링의 단점]
추천 시스템의 평가
| 실제 데이터 | 가린 데이터 | 추정한 데이터 |
|---|---|---|
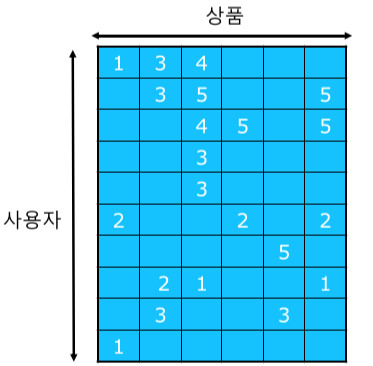 |
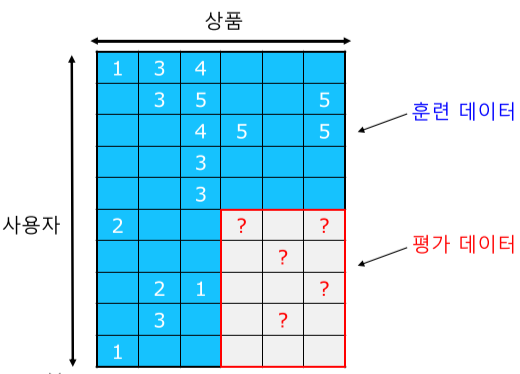 |
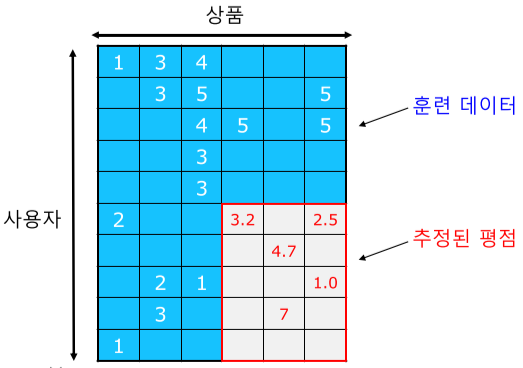 |
[fig. 추천 시스템의 평가 방법]
- 실제 데이터를 훈련(Training) 데이터와 평가(Test) 데이터로 분리한 뒤
- 평가 데이터를 가리고 추천 시스템으로 추정한 뒤
- 이를 실제 데이터와 지표를 비교하여 평가한다.
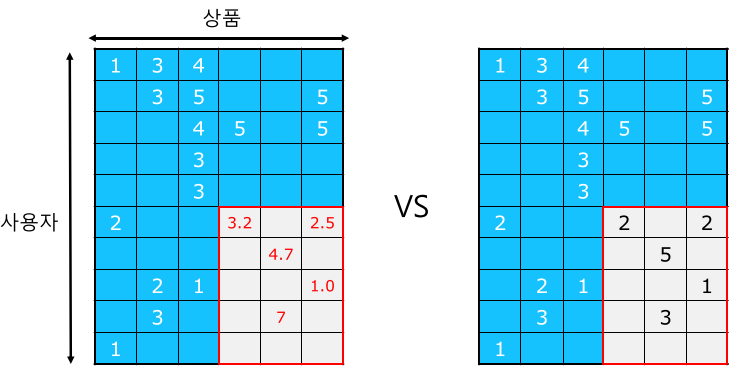
[img. 추정한 평가데이터 vs 실제 데이터]
오차를 측정하는 지표로 평균 제곱 오차(Mean Squared Error, MSE)와 평균 제곱근 오차(Root Mean Squared Error, RMSE)가 많이 사용됨.
\(MSE =\frac{1}{|T|}\sum_{r_{xi}\in T}(r_{xi}-\hat{r}_{xi})^2\\
RMSE = \sqrt{\frac{1}{|T|}\sum_{r_{xi}\in T}(r_{xi}-\hat{r}_{xi})^2}\\
where\ T: 평가\ 데이터\ 내의\ 평점들을\ 집합\)
[math. 추천 시스템의 오차 측정 지표 식]
이외에도 다음과 같은 지표 등이 사용됨.
- 추정한 평점으로 순위를 매긴 후, 실제 평점으로 매긴 순위와의 상관 계수
- 추천한 상품 중 실제 구매로 이루어진 것의 비율
- 추천의 순서 혹은 다양성까지 고려하는 지표
협업 필터링 구현
Lab의 [Graph-6]Collaborative_Filtering.ipynb 참조
그래프의 벡터 표현
정점 표현 학습
그래프의 정점들을 벡터의 형태로 표현하는 것, 정점 임베딩(Node Embedding)이라고도 부름.
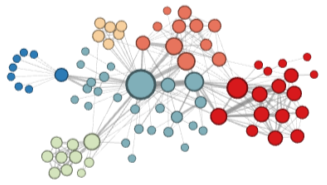
정점이 표현되는 벡터 공간을 임베딩 공간이라고 부름.
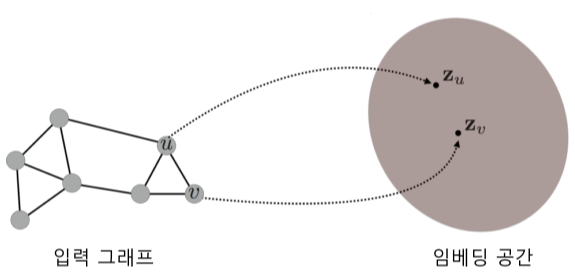
[img. 임베딩 공간의 예시]
정점 표현 학습의 입력은 그래프이며, 주어진 그래프의 각 정점 u에 대한 임베딩 벡터 표현 $z_u$가 정점 임베딩의 출력
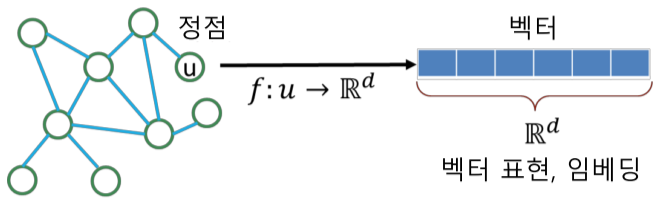
[img. 벡터 표현의 예시]
이러한 정점 임베딩의 결과로 벡터 형태의 데이터를 위한 도구를 그래프에도 적용할 수 있음.
- 분류기(로지스틱 회귀분석, 다층 퍼셉트론)
- 군집 분석 알고리즘(K-Means, DBSCAN)
- 정점 분류(Node Classification), 군집 분석(Community Detection)
정점간 유사도를 임베딩 공간에서도 보존하는 것을 목표로 하며, 유사도로는 내적(Inner Product)을 사용
\(similarity(u,v) \approx z_v^{\top}z_u=\left\|z_u\right\|\cdot\left\|z_v\right\|\cdot\cos(\theta)\)
[math. 두 정점 벡터의 내적==유사도]
- 두 벡터가 클수록, 같은 방향을 향할수록 큰 값을 갖게 됨.
- 이 이외에도 여러가지 유사도 측정 방법이 있음
즉 정점 임베딩은
- 그래프의 정점 유사도를 정의하는 단계
- 정의한 유사도를 보존하도록 정점 임베딩을 학습하는 단계
로 이루어짐
인접성 기반 접근법
두 정점이 인접할 때(둘을 직접 연결하는 간선이 있을 때) 유사하다고 간주하는 방법
인접 행렬(Adjacency Matrix) A의 u행 v열 원소 $A_{u,v}$는 원소 u와 v가 인접한 경우 1, 아니면 0이며, 이를 유사도로 가정

[img. 그래프의 인접행렬 표현]
손실함수(Loss Function)가 최소가 되는 정점 인베딩을 찾는 것이 목표이며, 이를 위해 (확률적) 경사하강법을 사용.
\(손실함수\ \mathcal{L} = \sum_{(u,v)\in V\times V}\left\|z_u^\top z_v - \sum_u A^k_{u,v}\right\|^2\\
\sum_{(u,v)\in V\times V} : 모든\ 정점\ 쌍에\ 대하여\ 합산,\\ z_u^\top z_v:임베딩\ 공간에서의\ 유사도,\ A_{u,v}: 그래프에서의\ 유사도\)
[math. 인접성 기반 접근법의 손실 함수(Loss Function)]
다만 이 방법은 정점 간의 거리가 고려되지 않는다.
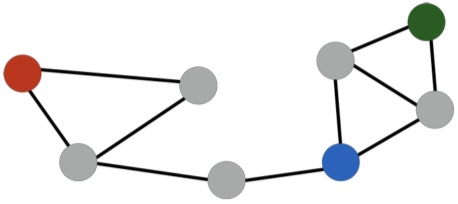
[img. 인접성 기반 유사도 판단의 한계 예시]
빨간색 정점과 파란색 정점의 거리는 3, 다른 군집 소속
초록색 정점과 파란색 정점의 거리는 2, 같은 군집 소속이지만 인접성만 고려할 시, 두 경우 유사도가 0 이다.
-> 인접성 기반은 군집과 거리 등의 속성을 무시한다.
거리/경로/중첩 기반 접근법
- 거리 기반 접근법
두 정점 사이의 거리가 충분히 가까운 경우 유사하다고 간주
'’충분히’‘의 기준 거리를 가정한 그보다 거리가 작거나 같으면 1, 크면 0으로 유사도를 간주
- 경로 기반 접근법
두 정점 사이의 경로가 많을 수록 유사하다고 간주
u와 v 사이의 경로는 u에서 시작해서 v에서 끝나야하며, 순열에서 연속된 정점은 간선으로 연결되어야 함.
두 정점 u와 v의 사이의 경로 중 거리가 k 인 것의 수를 $A^k_{u,v}$라고 할 때
- 이는 인접 행렬 A의 K 제곱의 u행 v열 원소와 같음.
[math. 경로 기반 접근법의 손실함수]
- 중첩 기반 접근법
두 정점이 많은 이웃을 공유할 수록 유사하다고 간주
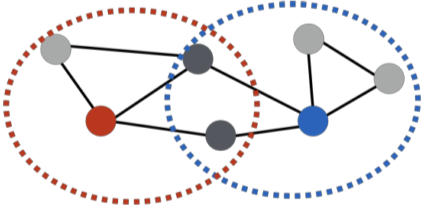
[img. 빨간색 정점은 파란색 정점과 2명의 이웃을 공유한다.(==유사도 2)]
\(공통\ 이웃\ 수\ S_{u,v}=|N(u)\cap N(v)|=\sum_{w\in N(u)\cap N(v)}1\\
손실함수\ \mathcal{L}=\sum_{(u,v)\in V\times V} \left\| z_u^{\top}z_v-S_{u,v} \right\|^2\\
N(x): 정점\ x의\ 이웃\ 집합\)
[math. 중첩 기반 접근법에서의 손실함수]
손실함수를 이용하며, 이때 공통 이웃수가 아닌 자카드 유사도 혹은 Adamic Adar 점수를 기반으로 사용할 수도 있다.
\(자카드\ 유사도(Jaccard\ Similarity): \frac{N_u\cap N_v}{N_u\cup N_v}\\
Adamic\ Adar\ 점수: \sum_{w\in N_u\cap N_v}\frac{1}{d_w}, d_w: 연결성\)
[math. 공통 이웃 수 대신 사용가능한 지표]
- 자카드 유사도(Jaccard Similarity) : 공통 이웃의 수 대신 비율을 계산
- Adamic Adar 점수 : 공통 이웃 각각에 가중치를 부여하여 가중합을 계산
- 그 이웃의 연결성이 클수록(=이웃이 많을 수록) 가중치가 낮은데, 유명한 사람을 연결한 경우는 큰 의미가 없는 경우가 많기 때문이다
- 트와이스를 팔로우한 두 사람은 관계없을지도 모르지만, 김철수씨를 팔로우한 두 사람은 친구일 확률이 높다.
임의보행 기반 접근법
한 정점에서 시작하여 임의보행을 할 시, 다른 정점에 도달할 확률을 유사도로 간주
- 임의 보행이란 현재 정점의 이웃 중 하나를 균일한 확률로 선택하며 이동하는 과정을 반복하는 것
시작 정점 주변의
- 지역적 정보 ( 무작위 보행시 시작 주변을 마구 돌아다닐 확률이 높으므로)
- 그래프 전역 정보 (거리나 제한을 두지 않으므로 마음대로 돌아다닐 수 있으므로)
둘을 모두 고려한다는 장점이 있음
임의 보행 기반 접근의 순서
- 각 정점에서 시작하여 임의보행을 반복 수행
- 각 정점에서 시작한 임의보행 중 도달한 정점들의 리스트를 구성
- 정점 u에서 시작한 임의보행 중 도달한 정점들의 리스트를 $N_R(u)$라고 함
- 정점의 중복 허용
- 정점 u에서 시작한 임의보행 중 도달한 정점들의 리스트를 $N_R(u)$라고 함
- 손실함수를 최소화하는 임베딩을 학습함
[math. 임의보행에서의 손실함수와 도달 확률]
-
임의 보행 확률 $P(v z_u)$는 (u에 도달할 확률(내적))/(전체 정점들 도달할 확률의 합(내적))으로 구한다. - 유사도 $z_u^{\top}z_n$가 높을 수록 도달 확률이 높음.
또한, 임의보행의 방법에 따라 다음과 같이 구분된다.
- DeepWalk
- 기본적인 임의보행, 현재 정점의 이웃중 하나를 균일한 확률로 선택하여 이동
- Node2Vec
- 2차 치우친 임의보행(Second-order Biased Random Walk)을 사용
- 현재 정점(v)과 직전에 머물렀던 정점(u)을 모두 고려하여 다음 정점을 선택
- 즉, 직전 정점의 거리를 기준으로 경우를 구분하여 차등적인 확률을 부여
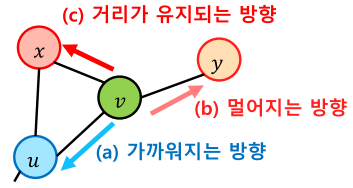
[img. 2차 치우친 임의 보행의 선택]
| Node2Vec | K-means 군집 분석 결과 |
|---|---|
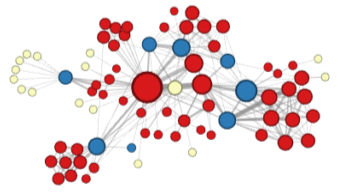 |
 |
| 멀어지는 방향에 높은 확률 부여 | 가까워지는 방향에 높은 확률 부여 |
| 정점의 역할(다리 역할, 변두리 정점 등)이 같은 경우 인베딩이 유사 | 같은 군집(Community)에 속하는 경우 임베딩이 유사 |
[fig. 부여하는 확률에 따라 다른 종류의 임베딩 획득]
손실 함수의 근사법
\(\mathcal{L}=\sum_{u\in V}\sum_{v\in N_R(u)}-\log(P(v|z_u))\\
P(v|z_u)=\frac{\exp(z_u^{\top}z_v)}{\sum_{n\in V}\exp(z_u^{\top}z_n)}\\
\sum_{u\in V}, \sum_{n\in V}: 중첩된\ 합 \rightarrow 정점\ 수의\ 제곱에\ 비례하는\ 시간이\ 소요\)
[math. 기존의 손실함수와 느린 이유]
기존 손실함수는 정점이 많은 경우 천문학적 수 이상의 연산이 필요하다.(1억의 정점은 10000조번 연산)
따라서 많은 경우 근사식을 사용함
\(P(v|z_u)=\frac{\exp(z_u^{\top}z_v)}{\sum_{n\in V}\exp(z_u^{\top}z_n)}\\
\approx \log(\sigma(z_u^{\top}z_v))-\sum^k_{i=1}\log(\sigma(z_u^{\top}z_v)),n_i\sim P_V\\
\sigma(x) : sigmoid\ 함수,\ P_V: 확률\ 분포\)
[math. 임의보행 확률의 근사식]
- 모든 정점에 대해서 정규화하지 않고 몇 개의 정점을 뽑아서 비교하며, 이를 네거티브 샘플이라고 함.
- 연결성에 비례하는 확률로 샘플을 뽑으며 많이 뽑을 수록 안정적인 학습이 이루어짐.
변환식 정점 표현 학습의 한계
앞에서 배웠던 방법들은 모두 변환식(Transductive) 방법으로, 학습의 결과로 정점의 임베딩 자체를 얻는다는 특성이 있다.
- 정점을 임베딩으로 변화시키는 함수, 즉 인코더를 얻는 귀납식(Inductive) 방법(9강에서 배움)과 대조
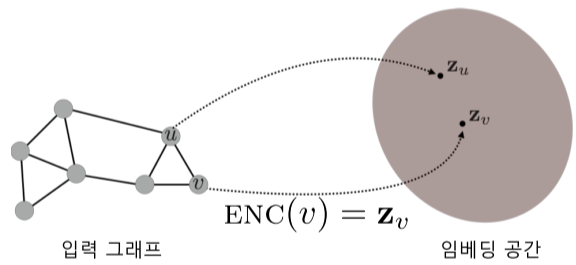
[img. 귀납식 방법 도식화]
변환식 임베딩의 한계
- 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩을 얻을 수 없음
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해야 함.
- 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용 불가능
- 엄밀히 말하면 3번째는 변환식 임베딩의 한계가 아닌, 위에 소개된 방법들의 한계이다.
이를 극복하기 위해 귀납식 임베딩 방법이 존재하며 대표적인 방법으로 그래프 신경망(Graph Neural Network)
Node2Vec을 사용한 군집 순석과 정점 분류
Lab의 [Graph-7]Node2Vec.ipynb 참조
추천 시스템 심화
넷플릭스 챌린지 소개
넷플릭스에서 수많은 사용자별 영화 평점 데이터 사용하여 성능을 10% 이상 향상시키는 것이 목표

[img. 당시 평균 제곱근 오차]
기본 잠재 인수 모형
잠재 인수 모형(Latent Factor Model)의 핵심은 사용자와 상품을 벡터로 표현하는 것
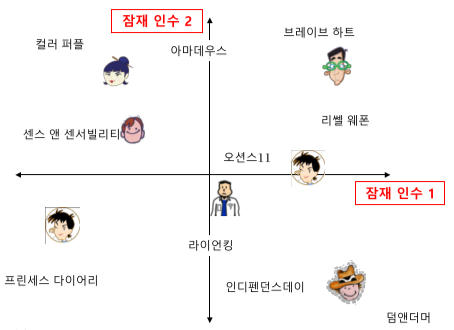
[img. 사용자와 영화를 임베딩한 예시]
잠재 인수 모형에서는 고정된 인수 대신 효과적인 인수(잠재 인수, Latent Factor)를 학습하는 것이 목표
임베딩의 목표는
사용자 x의 임베딩 $p_x$, 상품 i의 임베딩을 $q_i$라고 하며, 사용자 x의 상품 i에 대한 평점을 $r_{xi}$라 할때,
내적 $p_x^\top q_i$와 평점 $r_{xi}$를 유사하도록 하는 것이다.
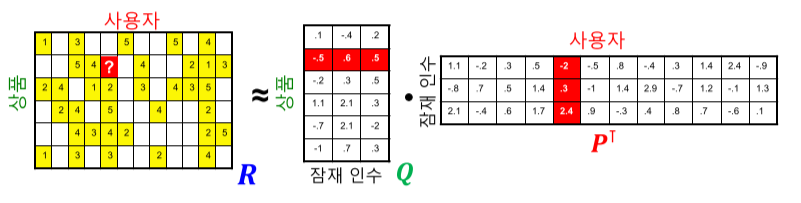
[img. 행렬 차원에서 본 임베딩의 목표]
- 위 행렬 차원에서는 R과 비슷해지는 Q과 $P^\top$을 찾는 것이 목표이다.
[math. 잠재 인수 모형에서의 손실 함수]
- 오른쪽의 모형 복잡도 항을 추가하여 정규화하여 과적합(Overfitting)을 방지한다.
- 과적합 이란 기계학습 모형이 훈련 데이터의 잡음(Noise)까지 학습하여, 평가 성능이 오히려 감소하는 현상
- 정규화를 통하여 절대값이 너무 큰 임베딩을 방지(너무 튀는 값 방지)
위 손실함수를 최소화 하기 위해 (확률적) 경사하강법을 사용함.
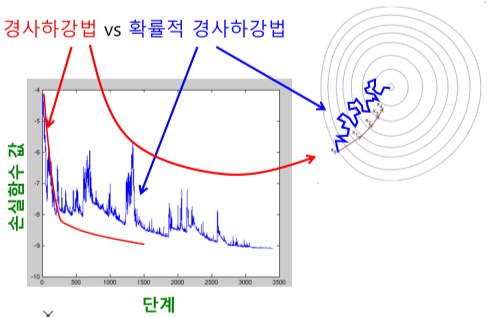
[img. 경사하강법 vs 확률적 경사하강법]
- 경사하강법: 손실함수를 안정적으로 하지만 느리게 감소(step은 더 확실히 들어가지만 연산이 느림)
- 확률적 경사하강법: 손실함수를 불안정하지만 빠르게 감소, 더 많이 사용됨
고급 잠재 인수 모형
단순히 사용자와 상품의 임베딩만으로 평점을 고려하는 것보다 더 현실적이고 오차가 적은 모형을 만들기 위해 두 가지를 추가로 고려하였다.
- 편향(bias)과 평균
- 사용자의 편향은 해당 사용자의 평점 평균과 전체 평점 평균의 차
- 나연의 평점이 4.0, 평균 평점이 3.7 이라면 나연의 사용자 편향은 0.3
- 다현의 평점이 3.5, 평균 평점이 3.7 이라면 다현의 사용자 편향은 -0.2
- 상품의 편향은 해당 상품에 대한 평점 평균과 전체 평점 평균의 차
- 영화 클레멘타인의 평점 평균이 3.0이고 평균 평점이 3.7이라면 상품 편향은 -0.7
- 시간적 평향
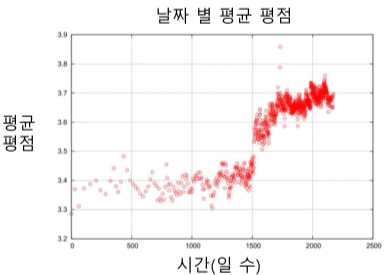
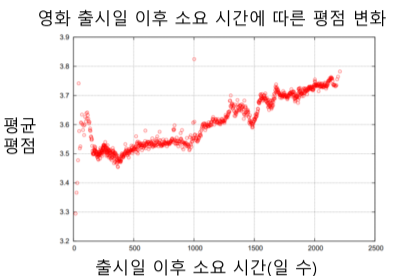
[img. 넷플릭스의 시스템 업데이트에 의한 평점 상승과, 영화 출시 이후에 평점 상승 경향 ]
- 평점이 시간에 따라 달라지는 경향을 추가로 고려
[img. 위 두가지를 고려하여 개선한 예상 평점]
\(\sum_{(i,x)\in R}{(r_{xi}-(\mu+b_x(t)+b_i(t)+p_x^\top q_i))^2}+{[\lambda_1\sum_x\left\|p_x\right\|^2+\lambda_2\sum_i\left\|q_i\right\|^2+\lambda_3\sum_x b_x^2+\lambda_4\sum_ib_i^2]}\)
[math. 최종적으로 개선된 손실 함수]
넷플릭스 챌린지의 결과

[img. 위의 방법들을 고려한 RMSE]
- 후에 추가로 앙상블 기법을 활용해 목표 오차에 도달하게 되고 같은 성능의 다른 팀보다 20분 제출이 더 빨랐던 BellKor 팀이 우승하게 된다.
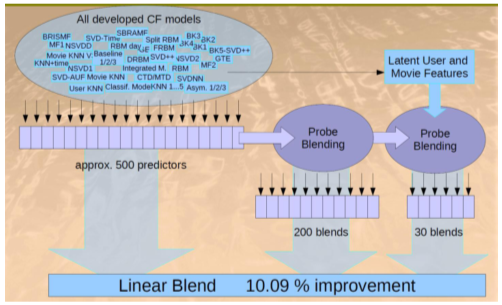
[img. 앙상블 기법]
Surprise 라이브러리와 잠재 인수 모형의 활용
Lab의 [Graph-8]Latent_Factor_based_Recommendation_System.ipynb 참조
그래프 신경망(Graph Neural Network) 기본
귀납식 임베딩은 다음과 같은 장점을 가진다.
- 학습이 진행된 이후에 추가된 정점에 대해서도 임베딩 획득 가능
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해둘 필요 없음
- 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 있음
$ENC(v) = 그래프\ 구조와\ 정점의\ 부가\ 정보를\ 활용하는\ 복잡한\ 함수$
[math. 귀납식 임베딩은 인코더 함수를 활용한다.]
그래프 신경망(GNN, Graph Neural Network)이란?
그래프 신경망(GNN, Graph Neural Network) : 출력으로 인코더를 얻는 귀납식 임베딩의 대표적인 방법
그래프 신경망의 구조
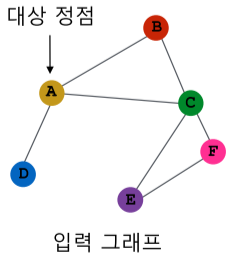
| 그래프 신경망은 *그래프(인접 행렬 형식A, | V | x | V | )와 정점의 속성(Attribute) 벡터($X_u$)*를 입력을 받음. |
- 속성은 속성의 갯수 만큼의 차원을 가지며, 성별, 연령, 정점 중신성, 군집 계수 등이 있음
| 입력 그래프 | 계산 그래프 |
|---|---|
 |
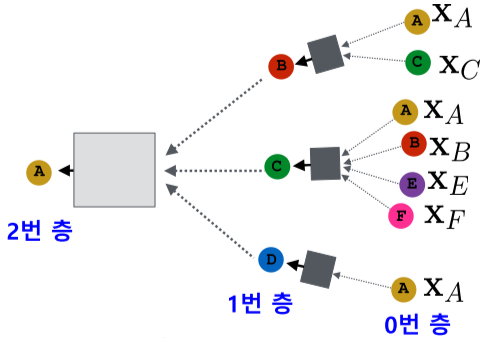 |
[fig. 대상 정점에 따른 그래프 신경망의 계산 그래프 ]
특정 정점의 임베딩을 얻기 위해 이웃 정점들의 임베딩을 집계하는 과정을 반복하는 방식
- 각 집계 단계를 층(Layer)라고 부르며, 각 층마다 임베딩을 계산
- 층의 갯수는 Hyperparameter인 듯?
- https://arxiv.org/pdf/1706.02216.pdf
- 최초의 0번 층의 입력은 각 정점의 속성 벡터($X_u$)를 이용
- 대상 정점 별 집계되는 구조를 계산 그래프(Computation Graph)라고 부름
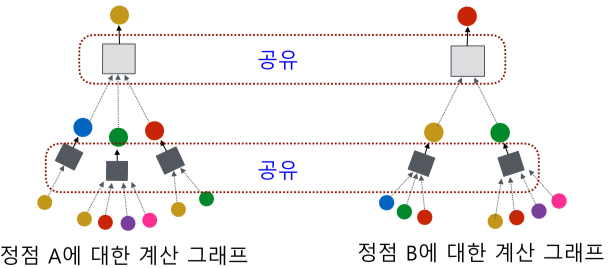
[img. 층 별 집계함수는 모두 공유함]
이웃의 정점의 임베딩을 이용해 특정 정점의 임베딩을 구할 때의 집계 함수를 이용하며, 각 층마다 모두 공유하며,
1) 이웃들 정보의 평균을 계산하고
2) 신경망에 적용
하는 단계를 거침.
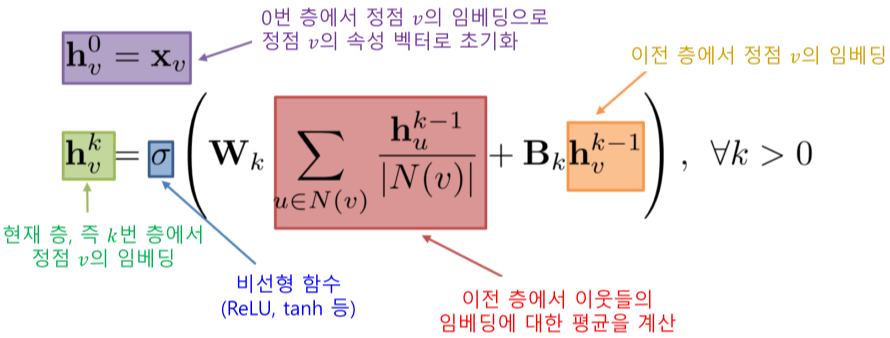
[img. k층에서의 임베딩($h^k_v$)을 구하는 집계함수 식]
마지막 층의 임베딩 결과 $h_v^k$가 해당 정점의 출력 임베딩이 되며, 학습 변수(Trainable Parameter)는 층별 신경망의 가중치인
- $W_k$
- $B_k$
이다.
그래프 신경망의 학습
그래프 신경망의 학습을 위해 가장 먼저 손실 함수를 결정해야 하며, 정점간 거리를 보존하는 것이 목표이다.
- 즉 임베딩 공간에서의 거리와 실제 그래프에서의 거리가 비슷한 것이 목표
- 주로 비지도 학습에서의 목표임
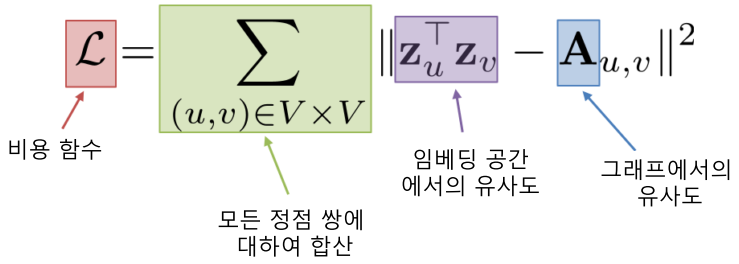
[img. 인접성 기반 유사도를 이용한 손실 함수 정의]
만약, 지도 학습인 후속 과제(Downstream Task)가 있다면,
해당 후속과제의 손실함수를 이용하는 것 또한 가능(종단종(End-to-End) 학습)
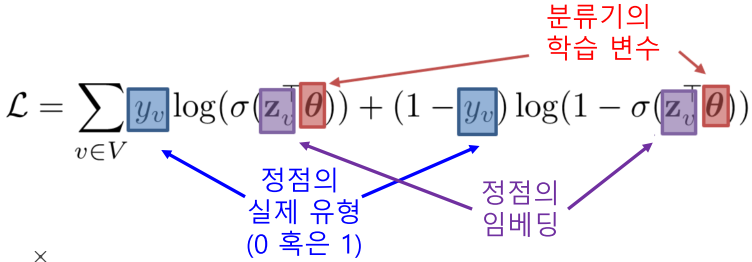
[img. 정점 분류기의 경우 손실함수를 교차 엔트로피(Cross Entropy)로 사용 가능]
- 정점 분류 문제는 정점이 어떠한 class를 가지는 가를 분류하는 문제(사람인가? 봇인가?)
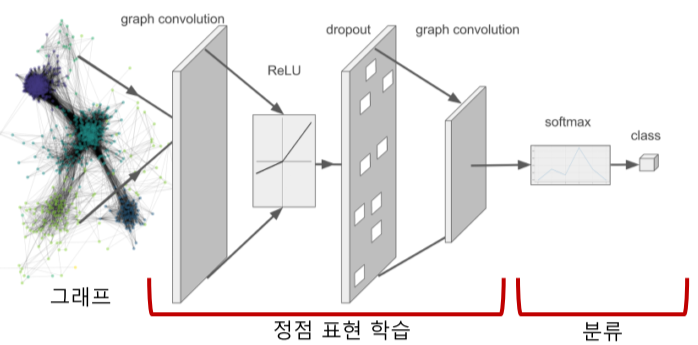
[img. 후속 과제의 학습 모델 예시]
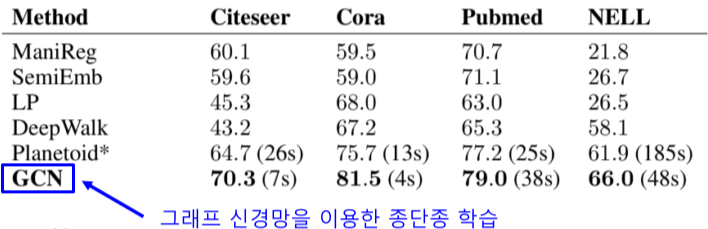
[img. GCN(아래에서 배울 Graph Convolutional Network)이 성능이 제일 높다.]
GNN End-to-End 학습이 변환적 정점 임베딩 + 분류기 학습 보다 정확도가 대체로 높음
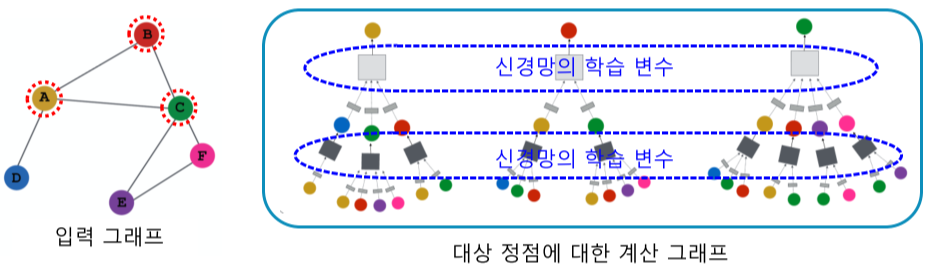
[img. 학습할 정점(A,B,C)와 그를 위한 학습 데이터 구성]
학습할 정점에 따라 다른 학습 데이터를 구성한 후, 오차역전파(Backpropagation)을 통해 손실함수를 최소화하며 학습 변수를 학습시키는 형식으로 학습이 진행된다.
그래프 신경망의 활용
그래프 신경망을 통해 이전에 언급했던 장점들이 발휘되게 된다.
- 이미 학습한 집계함수를 사용하여 학습에 사용되지 않은 정점의 임베딩을 얻을 수 있음
- 예를 들어[img. 학습할 정점(A,B,C)와 그를 위한 학습 데이터 구성]에서 이미 정점 A,B,C를 학습하기 위해 학습한 집계함수(구체적으로는 집계함수 학습변수의 가중치)를 다른 정점 임베딩에 사용할 수 있다.
- 학습이 끝난 이후 추가된 정점의 임베딩 또한 위와 마찬가지로 쉽게 구할 수 있음
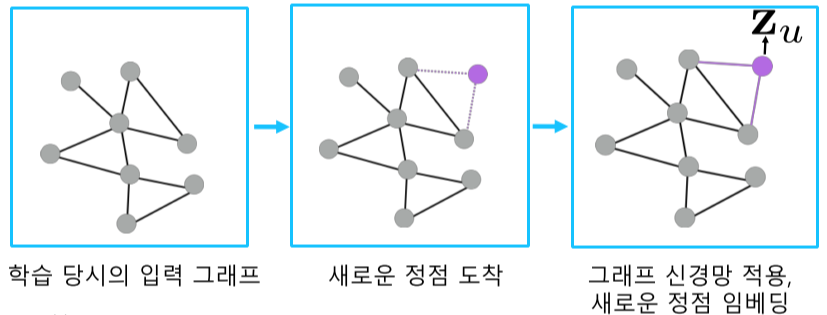
[img. 그래프의 정점 추가 시, 새로운 정점 임베딩의 학습]
- 학습 된 그래프 신경망의 집계함수를 새로운 그래프에 적용 가능
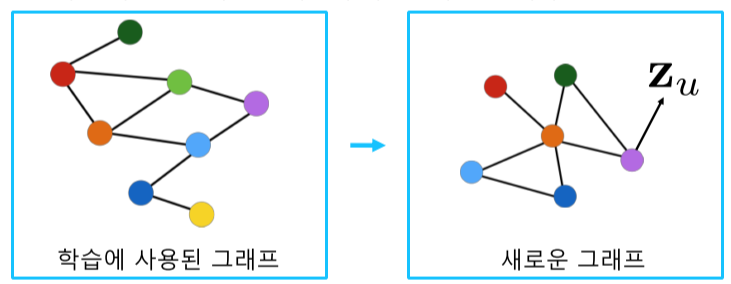
[img. 서로 다른 단백질의 상호작용 그래프를 예시로 들 수 있다.]
그래프 신경망 변형
- 그래프 합성곱 신경망(Grpah Convolutional Network, GCN)
그래프 합성곱 신경망(Graph Convolutional Network, GCN)은 집계함수로 기존의 GNN과 2가지가 다르다.
1) 학습변수가 GNN의 2개($W_k, B_k$)와 달리 $W_k$ 하나로 통합
| 2) 정규화 방법 : 현재 정점 v만의 연결성만 사용하던 GNN과 달리 현재 정점 v와 이전 정점 u의 기하 평균($\sqrt{ | N(u) | N(v) | }$)을 사용한다. |
- 기하 평균은 비선형 그래프에서 많이 사용됨, 그냥 산술 평균은 비선형 그래프에서 나올 수 없는 값이 나올 확률이 큼
\(h_v^k = \sigma\left(W_k\sum_{u\in N(v)\cup v}\frac{h_u^{k-1}}{\sqrt{|N(u)||N(v)|}}\right),\ \forall k \in \{1,\dots,K\}\)
[math. GCN의 집계함수]
- GraphSAGE
GraphSAGE의 집계함수 기존의 GNN과 2가지가 다르다.

[img.GraphSAGE의 집계 함수]
1) 이전 층에서의 자신의 임베딩과 이전 층에서 이웃들의 임베딩 연산 결과를 더하는 것이 아니라 연결(Concatenation)
-
GNN에서는 둘의 합을 구하였다($h_v^k=\sigma\left( W_k\sum_{u\in N(v)}\frac{h_u^{k-1}}{ N(v) }+B_kh_v^{k-1}\right)$).
2) 이웃들의 임베딩의 연산 결과를 평균을 통하여 구하는 것이 아닌, AGG 함수로 구함.
- AGG 함수는 평균, 풀링, LSTM 등이 사용됨
\(Mean:\ AGG = \sum_{u\in N(v)} \frac{h_u^{k-1}}{|N(v)|}\\ Pool:\ AGG = \gamma(\{Qh_u^{k-1},\forall u \in N(v)\})\\ LSTM:\ AGG = LSTM([h_u^{k-1},\forall u \in \pi(N(v))])\)
[math. GraphSAGE가 이웃들의 임베딩을 합치는 방법]
합성곱 신경망과의 비교
| 그래프 신경망 | 그래프 합성곱 신경망 |
|---|---|
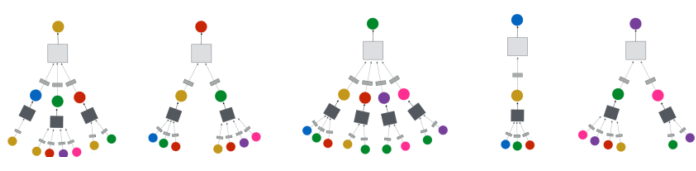 |
 |
| 집계하는 이웃의 수가 정점의 연결성에 따라 다름 | 집계하는 이웃의 수가 모두 동일 예시에는 주변 이웃 8개+ 자기자신 1개의 픽셀을 집계 |
[fig. 그래프 신경망 vs 그래프 합성곱 신경망]
그래프의 인접 행렬(A)에는 그래프 합성곱 신경망이 아닌 그래프 신경망만을 적용해야함.
- 인접행렬의 인접원소는 이미지와 달리 무작위로 구성되어있음,
- 따라서 주변 원소가 관계없는 임의의 원소인 경우가 많음
- 따라서 의미없는 정보가 이웃으로 집계가 되면 잘못된 결과가 나온다.
DGL 라이브러리와 GraphSAGE를 이용한 정점 분류
Lab의 [Graph-9]Using_GDL_Library-1.ipynb 참조
그래프 신경망 심화
그래프 신경망에서의 어텐션
이웃들의 정보를 동일한 가중치로 평균을 내는 기본 그래프 신경망과 연결성을 고려한 가중치로 평균을 내는 그래프 합성곱 신경망과 달리,
그래프 어텐션 신경망(Graph Attention Network, GAT)에서는 셀프-어텐션(Self-Attention)을 활용해 가중치 자체도 학습함.
- 이를 통해 이웃 별로 미치는 영향을 다르게 줄 수 있음.

[img. 그래프에 셀프 어텐션 구조를 적용]
각 층에서 정점 i로부터 이웃 j로의 가중치 $a_{ij}$는 다음과 같은 과정을 통해 계산 됨
| 단계 | 설명 | 수식 |
|---|---|---|
| 1 | 해당 층의 정점 i의 임베딩 $h_i$에 신경망 W를 곱해 새로운 임베딩을 얻습니다. | $\tilde h_i=h_iW$ |
| 2 | 정점 i와 정점 j의 새로운 임베딩을 연결한 후, 어텐션 계수 a를 내적. - 어텐션 계수 a는 모든 정점이 공유하는 학습 변수 |
$e_{ij}=a^\top[CONCAT(\tilde h_i,\tilde h_j)]$ |
| 3 | 2)의 결과에 소프트맥스(Softmax)를 적용 | $a_{ij}=softmax_j(e_{ij})=\frac{\exp(e_{ij})}{\sum_{k\in \mathcal{N}i \exp(e{ik})}}$ |
[fig. 그래프 어텐션 신경망 가중치 학습 단계]
또한, 여러 개의 어텐션을 동시에 학습하는 멀티 헤드 어텐션 또한 가능.
\({h}'_i=\underset{1\leq k\leq K}{CONCAT}\sigma\left(\sum_{j\in \mathcal{N}_i}a_{ij}^kh_jW_k\right)\)
[math. 멀티 헤드 어텐션에서의 정점 임베딩]
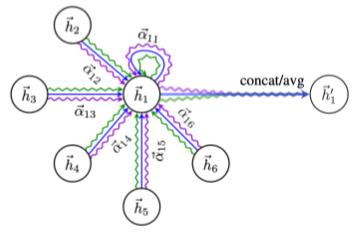
[img. 세 개의 어텐션을 사용한 GAT]
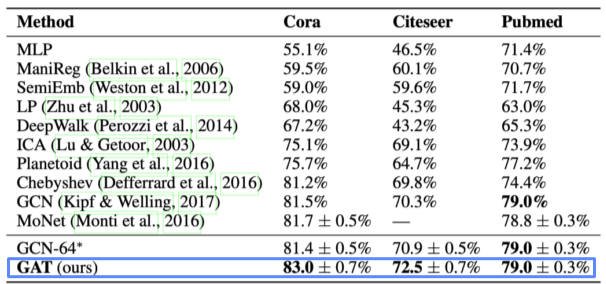
[img. 어텐션의 결과, 성능이 좋아짐]
그래프 표현 학습과 그래프 풀링
그래프 표현학습 또는 그래프 임베딩은 그래프 전체를 벡터의 형태로 표현하는 것
- 그래프 임베딩은 벡터 형태로 표현된 그래프 자체를 의미하기도 함
- 개별 정점이 아닌 그래프 자체를 벡터 형태로 표현한다는 점이 정점 임베딩과 다름
- 그래프 분류, 화합물 분자 구조 특성 예측 등에 활용
그래프 풀링(Graph Pooling) : 정점 임베딩들로부터 그래프 임베딩을 얻는 과정
- 정점 간의 평균 같은 단순한 방법보다 좋은 성능을 보임
- 그래프 풀링 방법 중 하나로 미분가능한 풀링(Differentiable Pooling, DiffPool)이 있다
- 군집을 임베딩 벡터로 바꾸어 가며 하나의 벡터로 바꾸는 방식
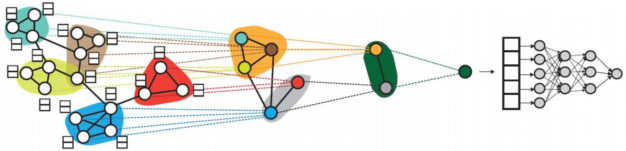
[img. 미분가능한 풀링의 도식]
미분 가능한 그래프 풀링에서는 다음과 같은 3가지 목적을 위해 기존의 GNN의 사용함.
- 개별 정점 임베딩 얻기
- 정점들을 군집으로 묶기
- 군집들을 합산해서 더 큰 군집을 만들기
지나친 획일화(Over-smoothing) 문제
지나친 획일화(Over-Smoothing) 문제는 그래프 신경망의 층의 수가 증가하며 정점 임베딩이 서로 유사해지는 현상이다.
- 정점 간의 거리가 생각보다 작기 때문에, 적은 수의 층만으로도 다수의 정점의 임베딩을 포함해 버리기 때문(작은 세상 효과)

[img. 지나친 획일화의 예시]
이로 인해 그래프 신경망의 층을 늘렸을 때, 오히려 성능이 감소하는 현상이 나타남
-
실제로는 다른 특색을 가진 정점을 비슷한 정점이라고 오판단하기 때문
-
보통 2~3개 층이 정확도가 가장 높음
잔차항(Residual)을 넣으면 조금 효과가 있지만 제한적이다.
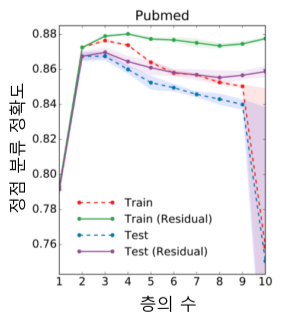
[img. 층 수에 따른 정확도 그래프]
\(h_u^{(l+1)}=h_u^{(1+1)}+h_u^{(l)}\)
[math. 잔차항(Residual)을 사용하는 방법]
지나친 획일화를 해결하기 위해 2가지 해결 방법에 대해 알아보자
- JK 네트워크(Jumping Knowledge Network)
마지막 층에 모든 층의 임베딩을 더해주는 방식

[img. JK 네트워크 도식]
지나친 획일화를 완전히 해결하는 방법은 아니며, 조금 완화해준다.
- APPNP(Approximate personalized propagation of neural predictions)
- 신경망 예측의 대략적인 개인화 전파?
- PPNP의 빠른 버전
0번째 층에서만 신경망을 적용, 그 이외에 층은 단순화한 집계함수를 사용
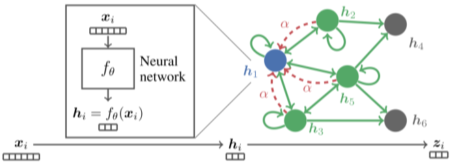
[img. APPNP 도식]
\(Z^{(0)} = H = f_\theta(X)\\
Z^{(k+1)} = (1 − \alpha)\tilde{\hat{A}}Z^{(k)} + \alpha H\\
Z^{(K)} = softmax\left((1 − \alpha)\tilde{\hat{A}}Z^{(K-1)} + \alpha H\right)\\
\alpha : teleport\ probability, H: prediction matrix, the teleport set,\\
X : feature\ matrix, f_\theta = a\ neural\ network\ with\ parameter\ set\ \theta\\
\tilde{\hat{A}}: the\ symmetrically\ normalized\ adjacency\ matrix\ with\ self-loops\)
[math. APPNP에서의 학습 과정]
- 정확히 말하면 PageRank 알고리즘 개선에 사용된 식이다.
- https://arxiv.org/pdf/1810.05997.pdf
층의 수가 늘어날 수록 성능 향상은 줄어들지만 층의 증가에 따른 정확도 감소 효과는 극복함.
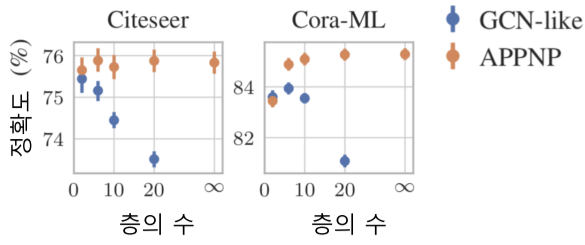
[img. APPNP의 성능]
그래프 데이터 증강(Data Augmentation)
그래프의 누락되거나 부정확한 간선을 보완하고, 임의 보행을 통해 정점간 유사도를 계산하여 유사도가 높은 정점 간의 간선을 추가하는 방법
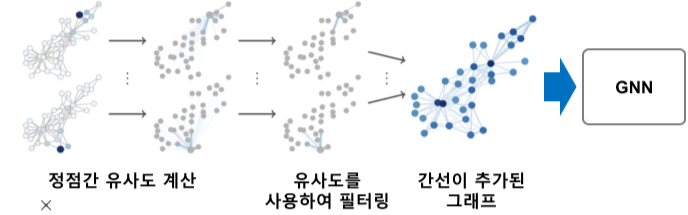
[img. 데이터 증강의 예시]
AI비전의 이미지 증강 처럼, 그래프 데이터 증강을 통하여 정확도를 개선할 수 있다.
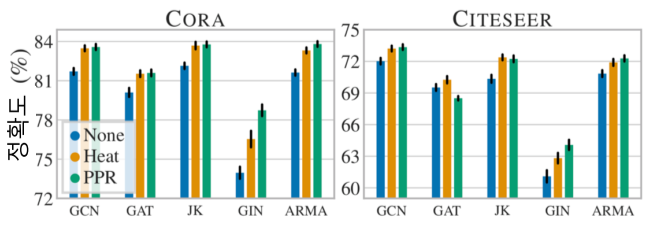
[img. 그래프 데이터 증강 효과]
GraphSAGE의 집계 함수 구현
Lab의 [Graph-10]Using_GDL_Library-2.ipynb 참조
_articles/AI/Graph/그래프 기본.md