avatar

풀스택 웹🌐 개발자 지망생 🧑🏽‍💻
➕ 인공지능 관심 🤖

Categories

Recent views

  • 1
  • 2
  • 3
  • 4
  • 5

딥러닝 기본

  1. Historical Review
  2. 뉴럴 네트워크(Neural Networks) - MLP
  3. Convolutional Neural Networks
  4. Modern CNN
    • Computer Vision Applications
    • Sequential Models - RNN
    • Transformer 모델
    • Generative Models(생성 모델)

    딥러닝 기본(Deep learning Basic)

    본 자료는 Naver BoostAI camp의 강의를 정리한 내용입니다

    Historical Review

    소개

    • 구현(코딩) 실력, 수학 스킬, 최신 논문 기술 등의 능력이 중요하다.

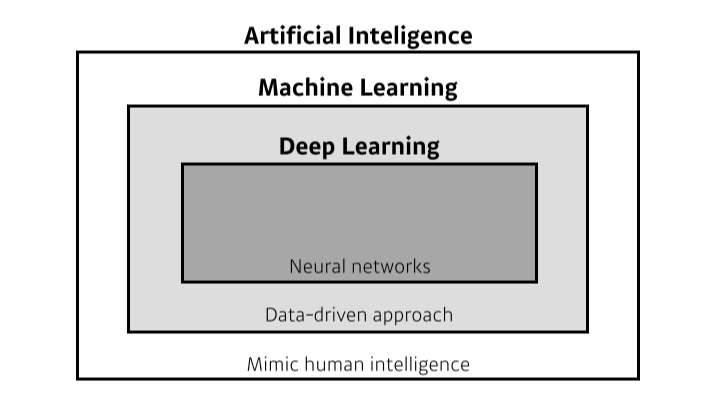
    [img 0. 인공지능의 대분류]

    • 인공지능 : 인간의 지능을 흉내
    • 머신러닝 : 데이터를 통해 인공지능을 학습

    • 딥 러닝 : 심층 신경망을 활용한 모델 이용하는 머신러닝, network를 깊게 쌓음

    • 딥러닝에 필요한 4가지 요소
      • 모델이 학습할 데이터 : 풀고자할 문제에 따라 필요한 데이터가 다르다.
        • Detection, Classification, Visual QnA 등
      • 데이터로 학습, 판단할 모델 : 데이터를 필요한 데이터로 바꿔주는 것
        • AlexNet, GoogLeNet, GAN 등
      • 모델 학습 방법인 loss 함수 : 모델을 학습하는 방법
        • 단순히 줄이는 것이 아니라 학습하지않은 데이터등에도 동작해야함.
        • MSE, CE, MLE 등
      • loss 함수를 최소화할 알고리즘 : loss 를 어떻게 줄일 것인가?
        • SGD, Adagrad 등이 있음
        • 추가로 Ensemble, MixUp, Dropout 등 테크닉이 있음

    딥러닝의 역사

    Denny Britz의 Deep Learning’s Most Importat Ideas - A Bref Historical Review를 참조함

    • 2012 - AlexNet: 최초로 인공지능 대회에서 1등을 한 DeepLearning 방법론. 시초
    • 2013 - DQN : 강화학습에 쓰인 방법론, Q Learning 접목, Deepmind의 작품
    • 2014 - Encoder/Decorder : 인공지능 번역에 쓰이는 방법론, 다른 언어의 연속으로 번역
    • 2014 - Adam Optimizer : 효과 좋은 optimizer, 왠만하면 잘된다라는 뜻이라고 함.
    • 2015 - Generative Adversarial Network(GAN) : 새로운 것을 생성하는 데 많이 사용하는 AI
    • 2015 - Residual Networks(ResNet) : 너무 깊어진 Network layer의 성능 저하를 막아줌
      • input을 추가로 넣어주는 것
    • 2017 - Transformer : attention 구조를 이용한 google의 방법론
    • 2018 - BERT(fine-tuned NLP models) : Transformer + bidirection 구조를 활용한 모델
      • Bidirectional Encoder Representations from Transformers의 약자
    • 2019 - Big Language Models(GPT-X) : OpenAI에서 만든 BERT의 Language 모델, 굉장히 많은 parameter로 이루어짐
    • 2020 - Self-Supervised Learning: SimCLR( a simple framework for contrastive learning of visual representations)의 줄인말, 학습 데이터 외의 라벨을 모르는 데이터를 활용, 지도 학습 + 비지도 학습
      • 시뮬레이터, 도메인 지식을 활용해 학습 데이터를 추가로 만드는 연구도 활발히 이뤄지는 중

    뉴럴 네트워크(Neural Networks) - MLP

    Neural Networks

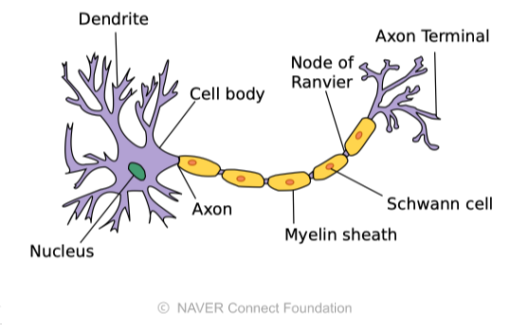
    [img 1. 두뇌 속의 신경망]

    동물의 생물학적 신경망에서 영감을 받은 컴퓨팅 시스템 - wikipedia

    • 생물학적 구조만 비슷할 뿐, 실제 작동원리와는 관계없음.

    • 행렬의 곱과 비선형 연산의 반복을 통하여 함수(논리)를 근사추정하는 것.

      • neural networks are function approximators that stack affine transformations followed by nonlinear transformations.

    Linear Neural Networks

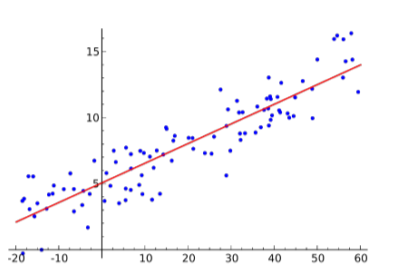
    [img 2. 선형 모델 그래프]

    • Data: $\mathcal{D} = {(x_i,y_i)}^N_{i=1}$ : input 값과 output 값이 각각 하나

    • Model: $\hat{y} = wx+b,\ \hat{y} : 모델의\ 예상치$ : 선형 그래프로 이루어짐

    • Loss: $loss =\frac{1}{N}\sum^N_{i=1}(y_i-\hat{y_i})^2$ : 실제 값과 얼마나 다른가에 대한 척도, 보통 MSE loss 함수로 loss 측정
    \[\frac{\partial loss}{\partial w} = \frac{\partial}{\partial w} \frac{1}{N}\sum^N_{i=1}(y_i - \hat{y_i})^2 = \frac{\partial}{\partial w} \frac{1}{N}\sum^N_{i=1}(y_i - wx_i-b)^2 =-\frac{1}{N}\sum^N_{i=1}-2(y_i-wx_i-b)x_i \\ \frac{\partial loss}{\partial b} = \frac{\partial}{\partial b} \frac{1}{N}\sum^N_{i=1}(y_i - \hat{y_i})^2 = \frac{\partial}{\partial b} \frac{1}{N}\sum^N_{i=1}(y_i - wx_i-b)^2 =-\frac{1}{N}\sum^N_{i=1}-2(y_i-wx_i-b)\]

    [math 2. backprogation을 이용한 w와 b의 편미분값 구하기]
    \(w = w - \eta\frac{\partial loss}{\partial w},\ b = b-\eta \frac{\partial loss}{\partial b}\)
    [math 2-1. loss 값을 줄이기 위한 새로운 w와 b 업데이트]

    • 이러한 방식으로 최적값을 구하는 것을 gradient descent라고 한다.

    • matrix 연산을 통하여 여러 차원의 input과 output 또한 해결 가능

      • matrix 연산은 두 벡터 공간 상의 변환을 의미함

    Activation function and Multi-layer Perceptron

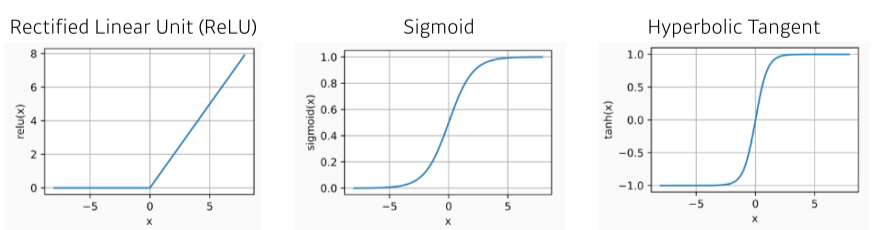
    [math 3. Activation fucntion의 종류와 그래프 모양]

    • 각 문제, 데이터마다 사용해야할 Activation function이 다르다.

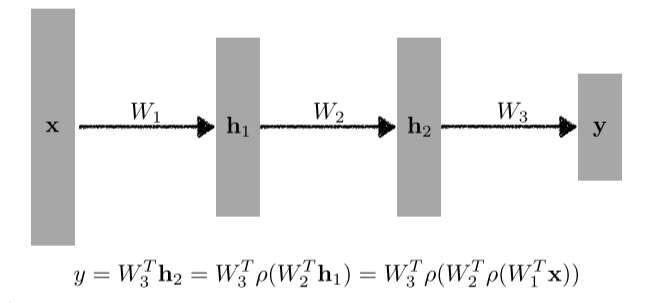
    [img 3. Multi-Layer Perceptron]

    • 이러한 여러 matrix 연산과 matrix 연산 사이의 activation function에 의해 nonlenar transform을 거쳐서 여러 층의 neural network가 된다.

    • 각 문제마다 loss function을 다르게 하게 된다.

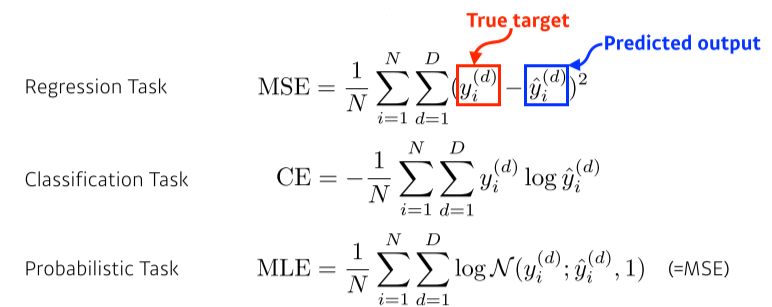
      • Regression Task : 선형 문제 (집 크기 vs 집 가격) 같은 문제에서는 MSE 등을 사용
      • Classification Task : 분류 문제(손글씨 숫자 구분) 같은 문제는 CE 등을 사용(가장 높은 확률의 class를 선택)
      • Probabilistic Task : 확률 문제(나이 맞추기 ) 같은 문제에는 MLE를 사용.

    [img 3. Multi-Layer Perceptron]

    • 실습은 https://colab.research.google.com/drive/14lEFtnt3kEn-LiwTKTwpUB-3VQ0Xx84W#scrollTo=3AS5BdrMw1E9 또는 mlp.ipynb 파일 참조

    Optimization

    관련 실습 : https://colab.research.google.com/drive/1p4H1mZpa41n3C8fQCtknQ0NfJGtEUIl6#scrollTo=B-uu6x8DFwZ9 혹은 optm.ipynb 참조

    용어의 정의

    • Gradient Descent(경사 하강): 반복 1차 미분을 통하여 loss의 국소 최소점을 찾는 알고리즘

    • First-order iterative optimization algorithm for finding a local minimum of a differntiable function.

    • Generalization(일반화): training error와 test error의 차이가 적음을 의미.

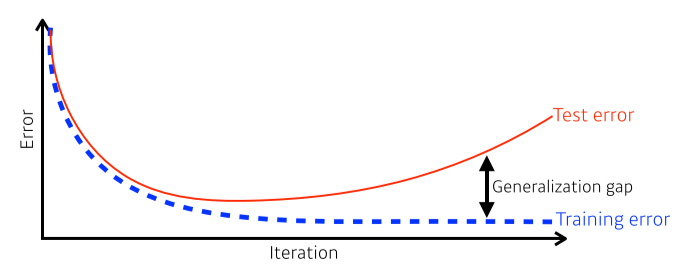
      [img 4. generalization의 그래프]

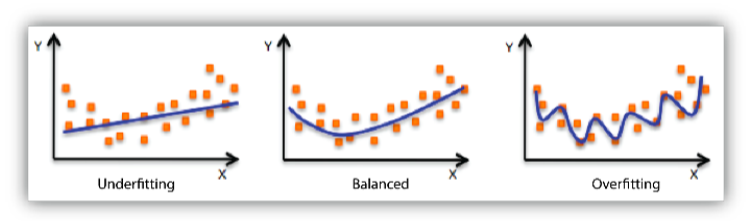
      [img 4-1. fitting의 도식화]

      • underfitting은 너무 training을 안해서 그래프가 적절하지 않음
      • overfitting은 너무 training을 많이해서 유연성이 없고, 해당 데이터 이외의 데이터에 부적합

    • Cross-validation(교차 검증, 또는 k-fold validation)

      • 데이터를 k개로 나눈 뒤 학습 데이터와 검증(validation) 데이터를 바꿔가며 hyper parametr를 정하는 모델 검증 기술

      • training, validation, test 데이터로 나누게 된다.

      • parameter : 최적해에서 찾는 값(weight, bias 등)
      • hyper-parameter: 내가 시작할 때 주는 값(loss function, learning rate 등)

    • Bias(편향) and Variance(분산도): 분산이 적은 것이 좋다.

      • 우리가 줄이는 cost는 사실 여러 부분으로 나뉘며 무엇을 줄일 지 생각해봐야한다.
      • noise가 많은 데이터면 bias와 variance를 둘다 줄이는 것이 힘드므로 골라야함

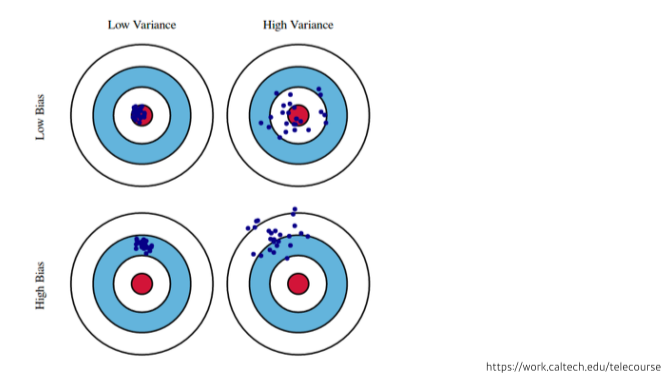
    [img 4-2. bias, variance 그림]
    \(Given\ \mathcal{D} = \{(x_i,t_i)\}^N_{i=1},\ where t = f(x)+ \epsilon\ and\ \epsilon \sim \mathcal{N}(0, \sigma^2)\\ \stackrel {\mathbb{E}\left[(t-\hat{f})^2\right]}{cost} = \mathbb{E}\left[(t-f +f-\hat{f})^2\right]=\dots=\stackrel {\mathbb{E}\left[(f-\mathbb{E}[\hat{f}]^2)^2\right]}{bias^2}+\stackrel {\mathbb{E}[(\mathbb{E}[\hat{f}]-\hat{f})^2]}{variance}+\stackrel {\mathbb{E}[\epsilon]}{noise}\)
    [math 4. cost(loss)의 구성]

    • bootstrapping : 학습 데이터를 일부만(예를 들어 80%만) 쓴 데이터를 각기 달리하여 여러개 만들어 랜덤 샘플링하여 학습시켜 보는것
      • 학습결과가 일정하면 데이터가 일정한 것이고, 결과가 각양각색이면 편차가 큰 것이다.
      • 이렇게 만든 여러 학습 데이터의 여러 모델의 평균이나 voting을 취하기도 함.(앙상블)
    • bagging(Bootstrapping aggregating) vs boosting
      • bagging : bootstraping으로 만들어진 여러개의 모델 (앙상블 기법)
      • boosting : 전체 데이터로 학습 해본 뒤, 해당 모델로 결과를 측정해 잘 예측못하는 데이터만 모아서 가중치를 더 크게 준 뒤, (랜덤 뽑기에 더 많이 할당?) 새로운 모델로 만든 뒤 이전 모델과 합치는 형식으로 진행 (앙상블 기법의 한 종류)

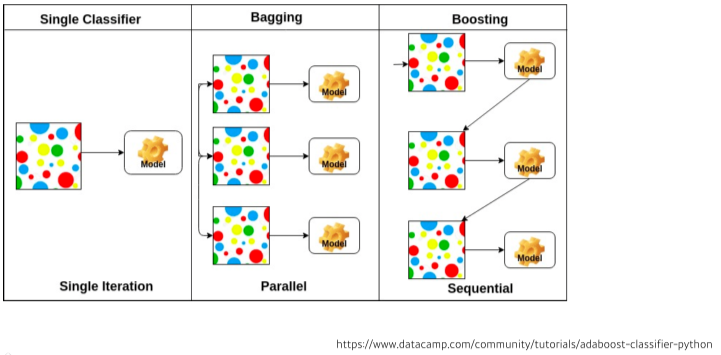
    [img 4-3. bagging boosting 그림]

    Practical Gradient Descent Methods

    Gradient Descent Methods
    • Stochastic gradient descent
      • update with the gradient computed from a single sample
      • 하나의 샘플마다 경사를 계산
    • Mini-batch gradient descent
      • update with the gradient computed from a subset of data
      • batch 크기의 샘플마다 경사를 계산
      • 가장 자주 사용함
    • Batch gradient descent
      • update with the gradient computed from the whole data
      • 한번에 모든 샘플을 활용하여 경사를 계산
    Batch-size Matters
    • 일반적으로 batch size가 너무 작으면 너무 오래걸리고, 크면 계산량이 너무 많다.
    • 연구 결과 batch-size가 작을 수록 유리하다는 것이 실험적으로 증명됨

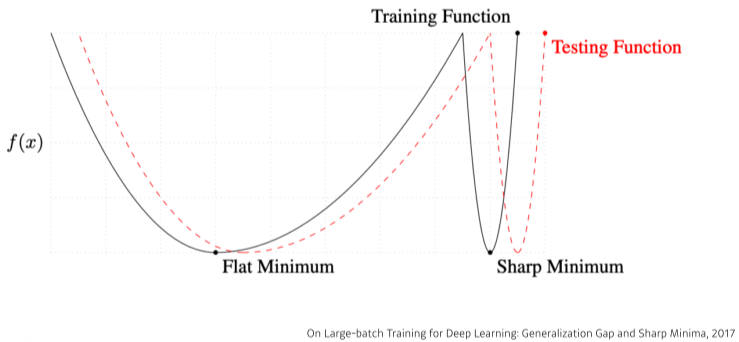
    [img 5. batch size가 작을 수록 좋은 이유]

    • batch size가 작으면 Flat Minimum, 크면 Sharp Minimum으로 도착하는 경향이 크다.
    • Flat Minimum은 test data 에서도 generalization이 잘되있지만 sharp minimu에서는 실제 testing 데이터와 갭이 크다.

    optimizer

    • 특성을 확인하고 상황에 따라 골라서 사용해야함
    Gradient Descent

    $W_{t+1} \leftarrow W_t - \eta g_t,\ \eta:learning\ rate,\ g_t:Gradient$

    [math 6. 경사하강법 ]

    • 가장 기본적인 방법
    • 적절한 learning rate를 잡는 것이 힘듦
    Momentum
    \[a_{t+1} \leftarrow \beta a_t + g_t\\ a_{t+1}:accumulation,\ \beta: momentum \\ W_{t+1} \leftarrow W_t - \eta a_{t+1}\\ \eta:learning\ rate\]

    [math 6-1. 모멘텀 개념]

    • 이전 gradient의 값이 영향을 조금 받은 gradient로 업데이트
    • 기본버전보다 조금 낫다.
    Nestrerov Accelerated Gradient
    \[a_{t+1} \leftarrow \beta a_t + \nabla \mathcal{L}(W_t-\eta \beta a_t) \\ \nabla \mathcal{L}(W_t-\eta \beta a_t):Lookahead\ gradient,\ \beta: momentum \\ W_{t+1} \leftarrow W_t - \eta a_{t+1}\\ \eta:learning\ rate,\ g_t:Gradient\]

    [math 6-2. NAG]

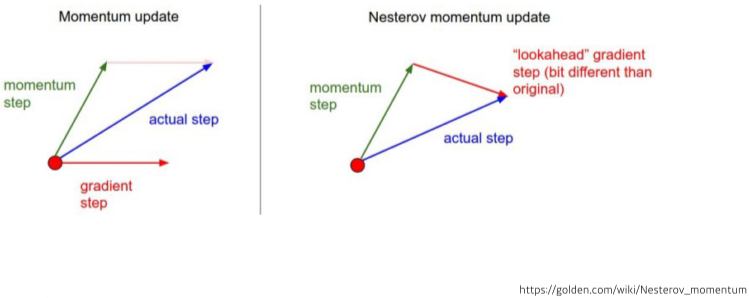
    [img 6. NAG와 Momentum 차이점]

    • momentum을 계량함
    • 최소 지점에 도달하는 것이 증명됨
    • 이전 gradient와 현재 그레디언트로 구하는 방법과 달리 이전 momentum gradient 벡터에서 현재 벡터로 이동한다는 다른점이 있음
    Adagrad
    \[W_{t+1} = W_t - \frac{\eta}{\sqrt {Gt+\epsilon}}g_t\\ G_t : Sum\ of\ gradient\ squares,\ \epsilon:for\ numerical\ stability\]

    [math 6-3. Adagrad 개념]

    • 파라미터의 변화량이 너무 적게 변하면 크게, 많이 변화해온 파라미터는 적게 learning rate를 잡아주어 조정해줌
    • 뒤로 가면 갈수록 G~t~가 커져서 무한대로 가까이 변해 거의 learning rate가 0으로 수렴되는 단점
    • $\epsilon$은 분모가 0이 되는 것을 막기 위해 주는 아주 작은 값.
    Adadelta
    \[G_t = \gamma G_{t-1} + (1-\gamma)g_t^2\\ W_{t+1} = W_t - \frac{\sqrt{H_{t-1}+\epsilon}}{\sqrt {G_t+\epsilon}}g_t\\ H_t=\gamma H_{t-1}+ (1-\gamma)(\Delta W_t)^2\\ G_t:EMA\ of\ gradient\ squares,\ H_t: EMA\ of\ difference\ squares\]

    [math 6-4. Adadelta 개념]

    • learning rate를 사용하지 않음.
    • window size를 정하고 해당 size step 만큼만 learning rate에 영향을 주게하여 무한대로 수렴하는 것을 막음
      • 예를 들어 윈도우 사이즈 10이번 11번 바뀌면 첫번째 파라미터 변화는 영향을 안주게 하고 11번째를 대신 추가.
    • 최근 100개의 값들을 모두 저장하면 메모리가 터지므로, exponential을 이용해서 구함
    RMSprop
    \[G_t = \gamma G_{t-1} + (1-\gamma)g_t^2\\ W_{t+1} = W_t - \frac{\eta}{\sqrt {G_t+\epsilon}}g_t\\ G_t:EMA\ of\ gradient\ squares,\ \eta: stepsize\]

    [math 6-5. RMSprop 개념]

    • adadelta에 stepsize만 추가, 그냥 경험적, 실험적으로 깨달은 식
    Adam
    \[m_t = \beta_1 m_{t=1} + (1-\beta_1)g_t\\ v_t = \beta_2v_{t-1} - (1-\beta_2)g_t^2\\ W_{t+1} = W_t - \frac{\eta}{\sqrt {v_t+\epsilon}}\frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t}m_t\\ M_t:Momentum,\ v_t: EMA\ of\ gradient\ squares,\ \eta: Step\ size\]

    [math 6-6. Adam 개념]

    • RMSdrop에 momenturm을 합친 개념
    • 무난하고 좋은 성능을 보인다.

    Regularization

    • generalization을 위해 학습에 제한을 거는 방법
    Early Stopping

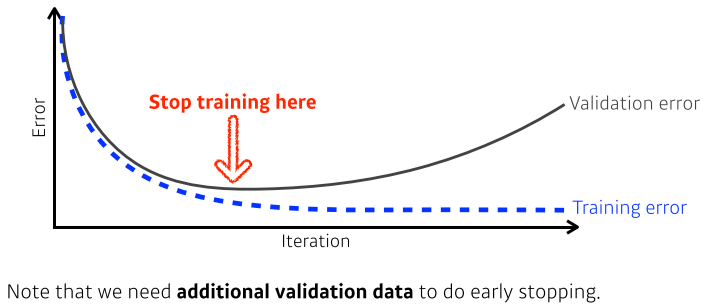
    [img 7. early stopping]

    • validation error와 training error를 비교하며 generalization gap이 가장 적을 때 stop하는 방법
    Parameter Norm Penalty
    \[total\ cost = loss(\mathcal{D;W}) + \frac \alpha 2 \left \| W \right \|^2_2\\ \frac \alpha 2 \left \| W \right \|^2_2:Parameter\ Norm\ Penalty\]

    [math 7. parameter Norm Penalty에 의한 cost 계산]

    • parameter들의 합이 너무 커지는 것을 방지
    • 부드러운 parameter일 수록 generalization이 좋은 경향이 있음
    Data Augmentation
    • 데이터가 적을 때는 오히려 전통적인 머신러닝이 성능이 좋지만, 데이터가 크면 클수록 최신 딥러닝이 좋다.
    • 문제는 데이터가 적으므로, 기존의 데이터를 여러가지 방법으로 바꾸어서 늘리는것
    • 이미지 데이터로 예시를 들면, 흑백, 일부 가림, 이미지 방향 반전 등이 있다.
    Noise Robustness
    • data Augmentation과 비슷하지만, 데이터 뿐만 아니라 weights에도 노이즈를 주어서 성능 향상
    Label Smoothing
    • 데이터 2개를 뽑아서 섞어 decision boundary를 부드럽게 해줌
    • mix-up 방법, cumMix 방법 등이 있음

    [img 7-1. Label Smoothing의 그림예시]

    • 성능이 되게 좋다.
    Dropout

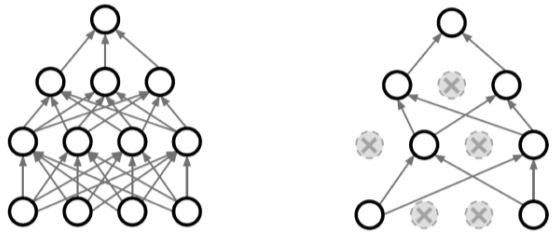
    [img 7-1. Label Smoothing의 그림예시]

    • 랜덤하게 neuron을 버린다.
    • 성능은 좋아지지만 수학적으로 증명이 되진 않음
    Batch Normalization
    \[\mu_B = \frac 1 m \sum_{i=1}^m x_i\\ \sigma^2_B = \frac 1 m \sum^m_{i=1}(x_i-\mu_B)^2\\ \hat{x}_i =\frac {x_i - \mu_B}{\sqrt{\sigma^2_B+\epsilon}}\]

    [math 7-1. Batch Normalization 계산]

    • 논란이 크지만 성능이 좋아짐.
    • layer들의 parameter들의 값을 평균과 분산을 이용하여 같은 값으로 바꿈.

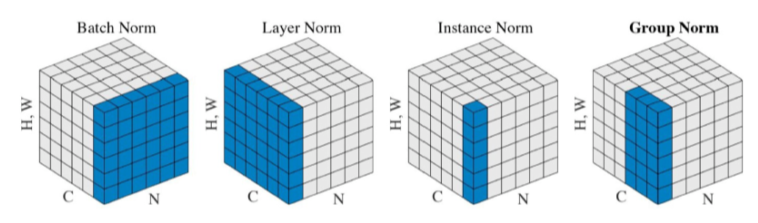
    [img 7-2. 다른 normalization의 종류]

    Convolutional Neural Networks

    Convolution 연산

    • 2개의 함수가 있을때 2개의 함수를 섞는 operator
    • 연속 공간, 이상 공간에 따라 수식 다름
    • I는 전체 공간, K는 필터

    \(\cdot Coninuous\ convolution:\ (f*g)(t) = \int f(\tau)g(t-\tau)d\tau=\int f(t-\tau)g(t)d\tau\\ \cdot Discrete\ convolution:\ (f*g)(t) = \sum^\infty_{i=-\infty} f(i)g(t-i)=\sum^\infty_{i=-\infty} f(t-i)g(i)\\ \cdot 2D\ image\ convolution:\ (I*K)(i,j) = \sum_m\sum_n I(m,n)K(i-m,j-n)=\sum_m\sum_n I(i-m,i-n)K(m,n)\\\)
    [math 8. Convolution operator]

    • 2차원 콘볼루션 연산의 예시.

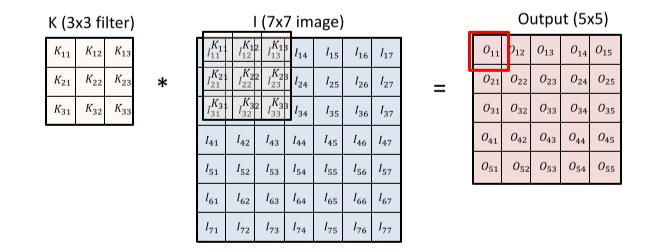
    [img 8. 2D image Convolution 그림]
    \(O_{11}=I_{11}K_{11}+I_{12}K_{12}+I_{13}K_{13}+I_{21}K_{21}+I_{22}K_{22}+I_{23}K_{23}+I_{31}K_{31}+I_{32}K_{32}+I_{33}K_{33}+bias\\ O_{12}=I_{12}K_{11}+I_{13}K_{12}+I_{14}K_{13}+I_{22}K_{21}+I_{23}K_{22}+I_{24}K_{23}+I_{32}K_{31}+I_{33}K_{32}+I_{34}K_{33}+bias\\ O_{13}=I_{13}K_{11}+I_{14}K_{12}+I_{15}K_{13}+I_{23}K_{21}+I_{24}K_{22}+I_{25}K_{23}+I_{33}K_{31}+I_{34}K_{32}+I_{35}K_{33}+bias\\ O_{14}=I_{14}K_{11}+I_{15}K_{12}+I_{16}K_{13}+I_{24}K_{21}+I_{25}K_{22}+I_{26}K_{23}+I_{34}K_{31}+I_{35}K_{32}+I_{36}K_{33}+bias\)
    [math 8-1. 2D image Convolution operation]

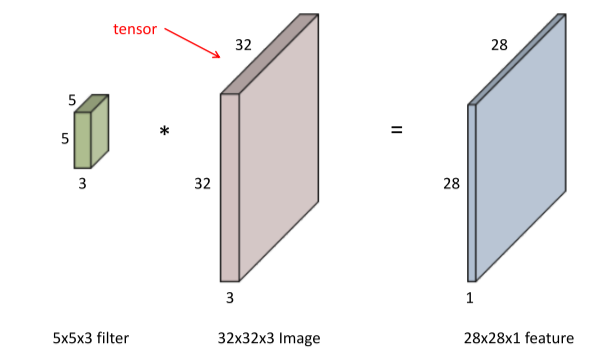
    [img 8-2. 2D image Convolution filter operation]

    • 2차원 이미지의 경우 tensor로 표현되며, 보통 rgb로 계산 시 뒤의 X3(R,G,B)은 생략이 된다.
    • 즉 5X5 convolution 연산은 기본적으로 5x5x3에서 x3이 생략된 것이다.
    • 계산 결과는 x1이 된다.

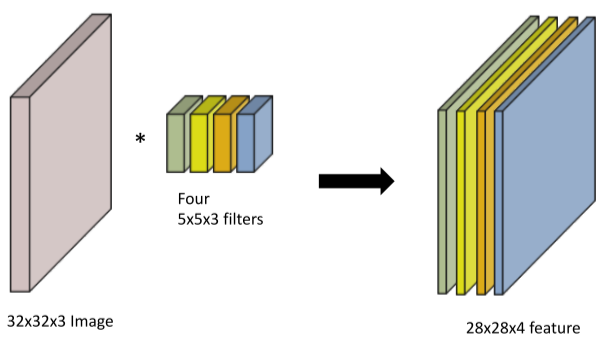
    [img 8-3. 2D image Convolution featuremap]

    • feature map을 연산할 때 여러 층의 feature가 나오는 방법은 여러겹의 필터를 곱하여 만드는 것이다.

    maxpool2d층 원리

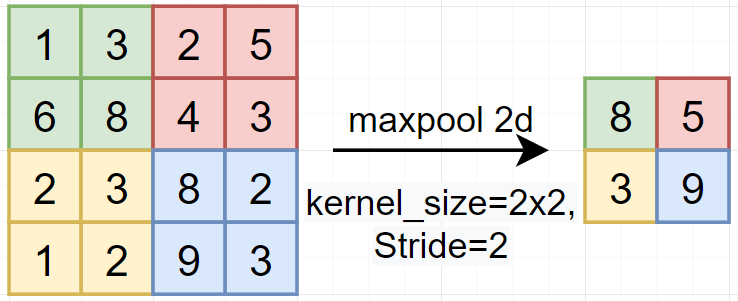
    [img. Maxpool 2d층 예시]

    • 각 구역을 kenelsize와 stride 만큼 나누어 가장 큰값을 취함
    • Max값을 취하는 Maxpool이외에도 평균값을 취하는 averagepool등도 있다.
    • featureamp의 크기가 줄어들어 성능을 줄이고 특징을 두드러지게 할 수 있다.
    • 다만, 공간 정보(위치, 방향, 비율)등이 모호해 지기도 한다.

    CNN 구조와 용어

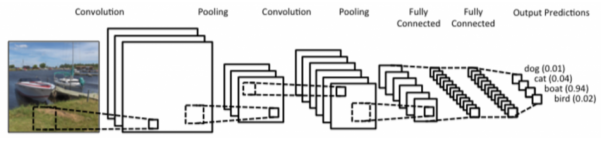
    [img 8-4. CNN 구조]

    • Convolution과 pooling layer는 feature extraction을 하는 역할
    • Fully connected Layer는 decision making(ex) classification)을 위한 층
      • 고전적인 CNN와 달리 최근에는 파라미터 수를 줄이기 + generalization 성능 향상을 위해 FCL을 줄이는 추세
    1. Stride

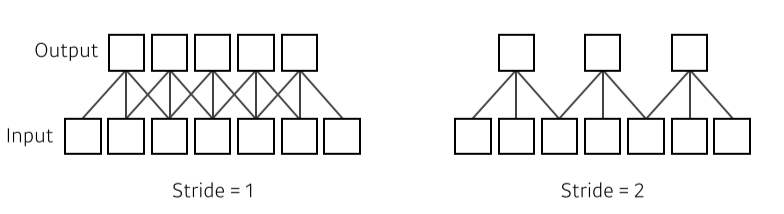
    [img. Stride 1과 2의 차이 그림]

    • pixel을 뛰어넘는 수, filter의 밀도,
    • filter가 stride 수 만큼 pixel을 넘어가며 생성한다.
    • 2차원의 경우 x,y 2개로 설정 가능
    1. Padding

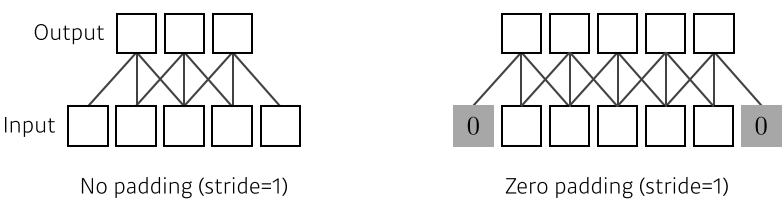
    [img. padding의 유무 차이 그림]

    • Stride 등으로 인해 외부로 나가는 픽셀을 padding으로 추가함
    • zero padding은 0을 넣는다는 의미, 이로써 input과 output의 space dimension이 같아짐

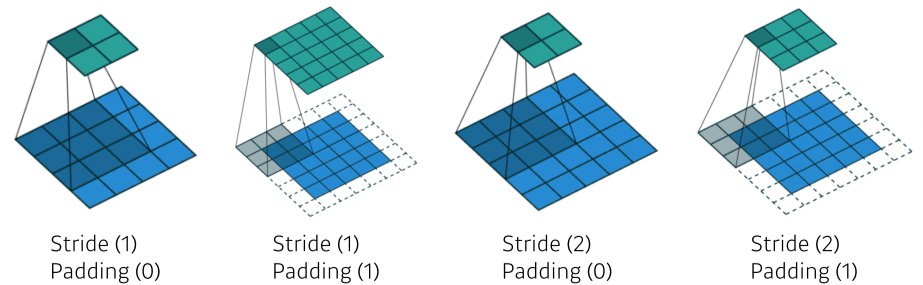
    [img. stride, padding의 예시]

    Convolution Arithmetic

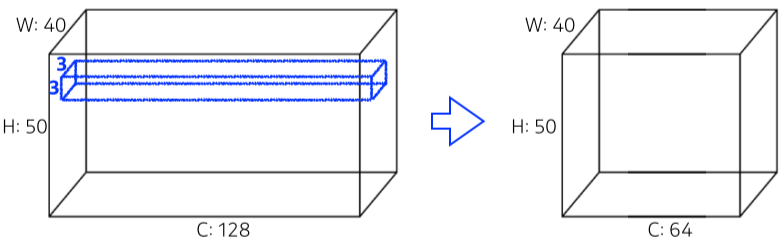
    [img. $3 \times 3$ kernel, Padding 1, Stride 1 의 연산 parameter 계산 예시]

    • parameter의 수는 가중치의 수

    • convolution layer의 학습 파라미터 수는 (필터 폭 X 필터 높이 X 입력 채널 수 X 출력 채널 수)로 계산

    • 위 예시는 $3 \times 3 \times 128 \times 64 = 73,728 $ 개의 학습 파라미터 수

    • Max pooling layer는 parameter output이 없다.
      • 메모리 성능 제한 때문에 2개로 나누어 trainig 하는 layer?
      • 그러므로 나뉜 수만큼 곱해주면 된다.

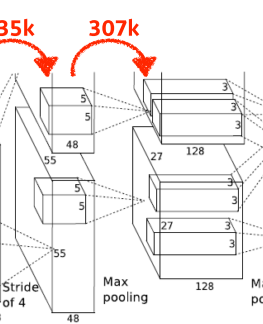
    [img. convolution 연산 추가 예시]

    • $5 \times 5 \times 48 \times 128*2 \approx 307k$
    • 굳이 정확히 숫자를 세는 것이 아니라 대략적인 양(마치 알고리즘의 big O 표기처럼) 성능을 측정할 수 있어야 한다.

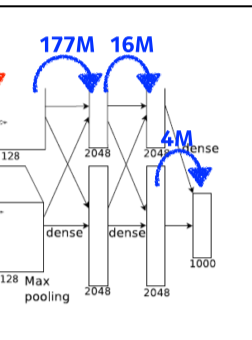
    [img. dense layer (fully connected layer) 연산 예시]

    • input의 neuron과 output의 neuron의 수를 곱한 만큼이다.

    • $13 * 13 * 128 * 2 \times 2048 *2 \approx 177M$

    • $2048 * 2 \times 2048 *2 \approx 16M$
    • $2048*2 \times 1000 \approx 4M$
    • Convolution operator는 같은 kernel을 연산에 쓰면서 parameter가 공유되므로 비교적 적다.
    • 1000배 이상의 parameter가 fully connected layer에 쓰이므로 이 부분을 줄이는 추세이다.

    1x1 convolution를 활용한 최적화

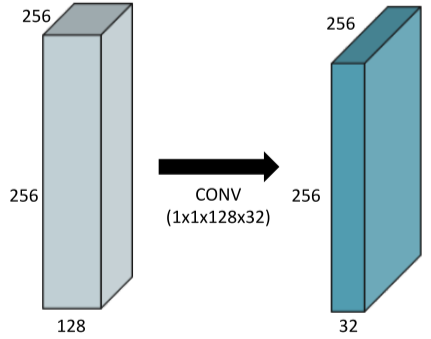
    [img. 1x1 convolution 적용에 의한 차원(filter)의 감소 효과]

    • 1x1 convolution layer 연산을 통하여 차원(filter)를 감소시켜 parameter 수를 줄이며, 층 수는 늘릴 수 있다.
    • bottleneck 구조의 원리

    Modern CNN

    • ~2018년 까지의 CNN 기술
    • ImageNet Large-Scale Visual Recognition Challenge 위주
      • Classification, Detection, Localization, Segmentation 등의 부문이 있음
    • 딥러닝의 최근 Error rate는 3.5% 이하로 인간의 5.1% 보다 에러가 적다.
    1. AlexNet

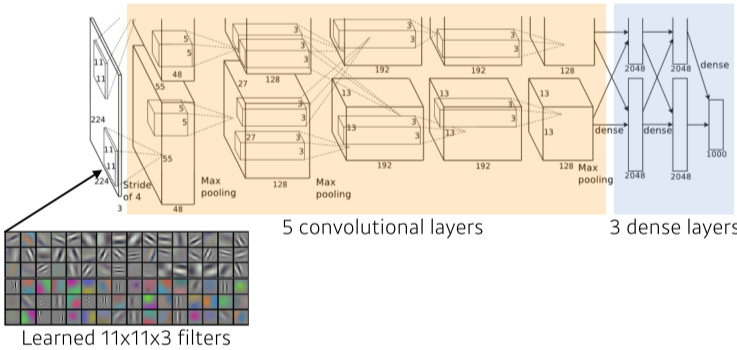
    [img. AlexNet 구조]

    • 컴퓨터 성능의 한계를 극복하기 위해 네트워크를 2개의 길로 나눈 8단의 layer.

    • 11x11x3 filter 사용
      • fitler의 크기가 클수록 convolution 연산 시, 고려되는 input의 크기(receptive field)가 커짐
      • receptive field : feature map 추출시 고려 가능한 입력의 spacial dimension.
      • 단, parameter의 수가 커짐
    • ReLU 활성 함수 사용.

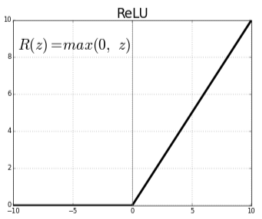
    • [img. Relu 함수, 0 이하는 0으로 바꾼다.]
      • 선형 모델의 장점, 학습이 용이, generalization 효과가 좋고, Vanishing gradient problem 극복
    • 2개 GPU 사용, Data augmentation, Dropout 활용
      • 그 외에도 Local Response normalization, Overlapping pooling 활용
    1. VGGNet

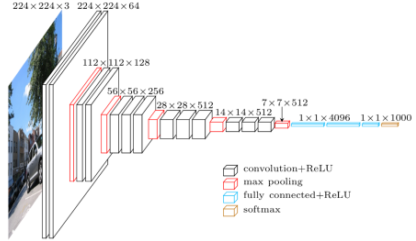
    [img.VGGNet 구조]

    • 3x3 convolution filter를 활용하여 파라미터 수 줄임

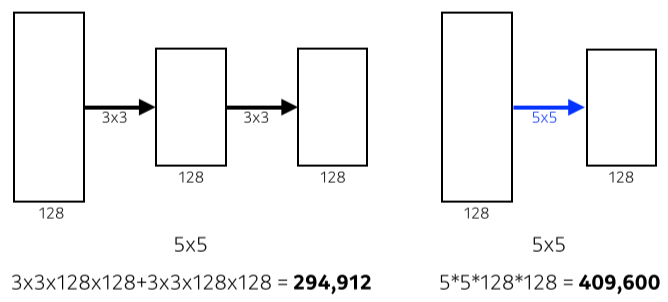
    • [img. 3x3 filter 두번 사용 vs 5x5 filter 한번 사용 파라미터 수 비교]

      • 필터를 통해 보는 input field의 크기는 같으나 2번 걸침으로 써 파라미터의 수는 줄일 수 있다.
      • 이 방법을 통해 보통 최대 7x7 필터를 넘지 않는다.

    • Dropout과 1x1 convolution을 dense layer에 활용

    • 16층 버전(VGG16), 19층 버전(VGG19)이 있음

    1. GoogleNet

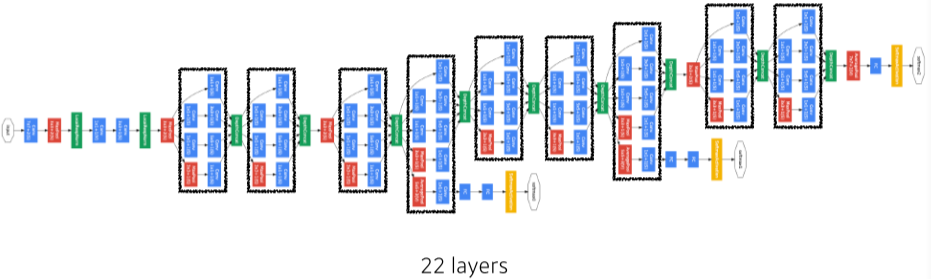
    [img. googlenet 구조]

    • NIN 구조(Network in Network) : 네트워크 내부에 모듈 형식의 작은 네트워크들의 반복이 존재

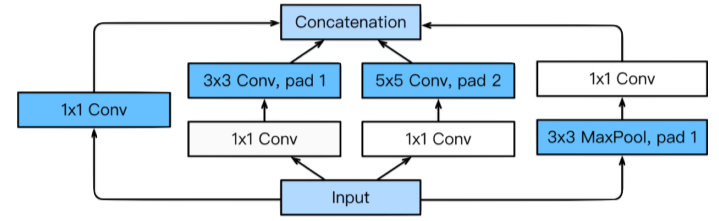
    • Inception blocks: 여러개로 퍼졌다고 다시 합쳐지는 블록

      [img. inception 모듈]

      • 여러 개의 responsed를 추출 가능

      • 1x1 Conv layer에 의해 파라미터의 수 감소.

      • 채널 방향의 차원을 줄이는 효과가 있음

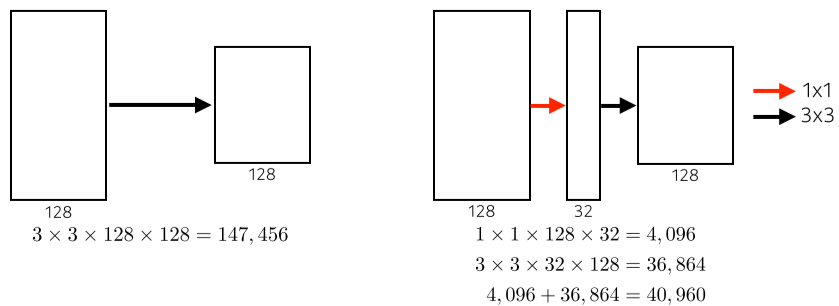
      [img. 1x1 convolution의 채널 감소 효과에 의한 파라미터 수 감소]

    • VGGNet, AlexNet에 비해 layer는 깊지만 파라미터 수는 오히려 적음

    1. ResNet

    • 깊은 층을 가진 DNN의 training error와 test error의 갭을 줄이고 학습을 용이하게 함.

    • 이를 통해 깊은 층의 DNN을 활용할 수 있게 해줌.

    • parameter 수는 줄고, 성능을 늘어나기 시작함

    • Residual connection (or Identity map)

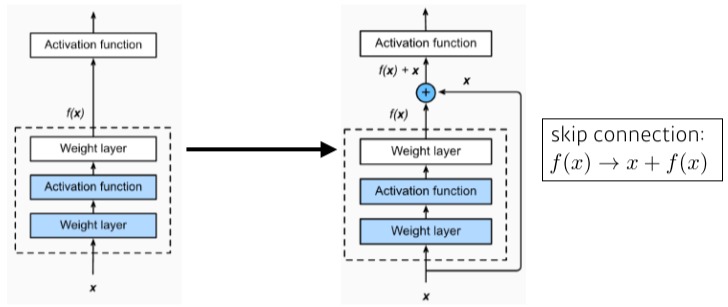
      • [img. identity map(residual map) 비교]

      • 출력 값을 일부 layer 너머의 출력에 더해 줌(skip connection)

      • 위 처럼 더해주는 simp shortcut 방식과 1x1 conv layer를 거쳐서 더해주는 Projected shortcut 방식(차원을 맞춰줘야 더 해지므로)이 있다.

      • 일반적으로 convolution layer 다음에 batch Norm, activation 함수 순으로 배치되며, Residual 합산은 batch Norm 뒤에, activation 앞에서 이루어진다.

        • 논란이 있으며, 순서가 바뀌어야 성능이 좋아질 때도 잇다.

    • Bottleneck architecture

      • 1x1 conv layer을 통해 input channel을 줄여서 parameter 수를 줄이고, 다시 채널을 늘려서 값을 더할 수 있게 함.

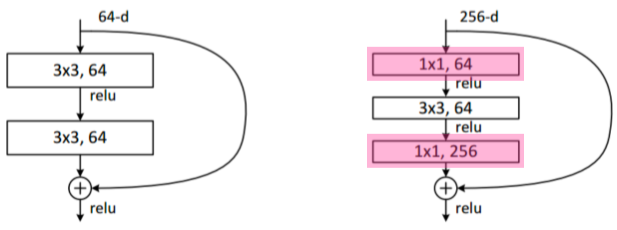
    [img. bottleneck architecture 그림]

    1. DenseNet

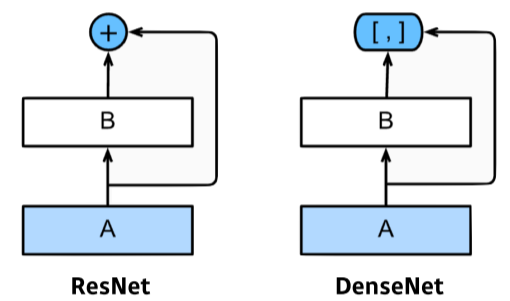
    [img. Resnet과 DenseNet 차이]

    • Resnet과 달리 결과값을 더하는 것이 아닌 concatenation 하는 방식
    • 채널이 점점 기하 급수적으로 커지므로, 중간에 한번씩 채널을 줄여줌
      • Dense Block : layer결과를 concatenate하여 채널을 늘림
      • Transition Block : batchnorm과 1x1 conv, 2x2 avgPooling을 통하여 채널 수 줄임
      • 위 두 block의 반복
    • 간단하고 성능이 좋다.

    Computer Vision Applications

    Semantic Segmentation

    • 이미지 내부의 일부(픽셀)를 물체로써 식별하는 문제
    • 자율 주행에서 사람, 인도, 자동차 등을 식별하는 등에 사용

    Fully Convolutional Network(FCN)

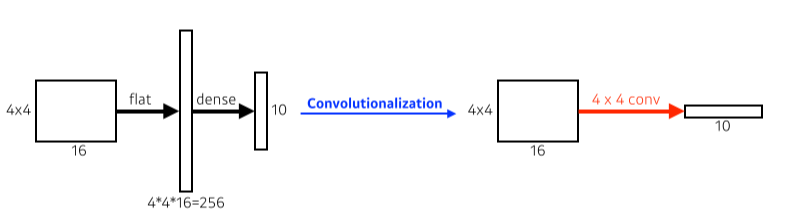
    [img. 기존의 CNN vs Fully Convolutional Network]

    • dense layer을 거치지 않고, convolution layer로 바꾸어 결과의 크기를 10이 아닌 차원의 수를 10으로 만드는 것을 convolutionalization이라고 한다.

    • 양쪽 다 parameter 수는 똑같이 4x4x16x10 = 2560으로 같다.

    • 하지만 이를 통하여 원본보다 size가 줄어든 heat map을 구할 수 있다.

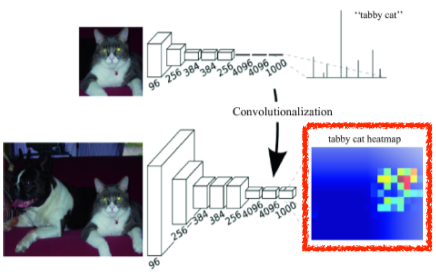
    [img. convolutionalize 를 통한 heat map 생성, 고양이의 추정위치 확인이 가능해짐. ]

    Deconvolution(conv transpose)

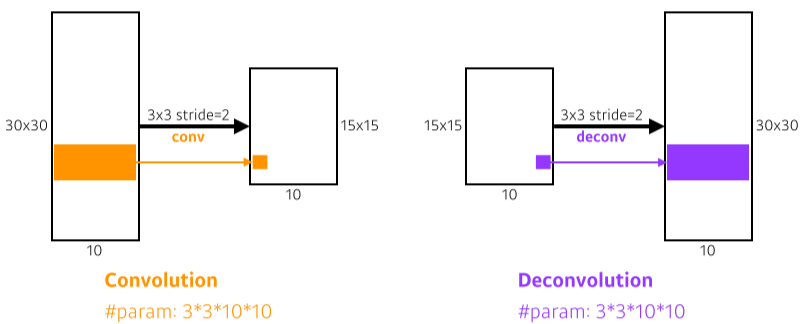
    [img. Deconvolution 개념]

    • 위의 줄어든 size를 원래대로 돌리기 위해 Deconvolution을 진행할 수 있다.
    • 원래 픽셀을 그대로 돌려주진 않으나 원본 크기로 돌아가게 된다.

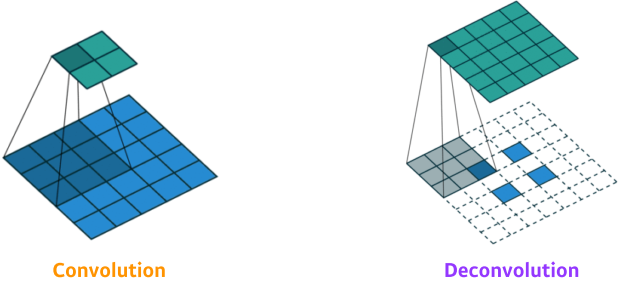
    [img. Deconvolution의 도식화]

    Detection

    • 이미지 내 물체의 바운딩 박스를 찾는 문제

    R-CNN

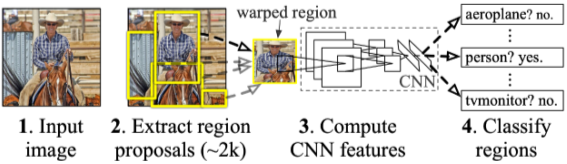
    [img. R-CNN의 절차와 예시]

    1. 이미지에서 Selective search를 통해 물체로 추정되는 부분의 bounding box를 bounding box regression을 통하여 전부 뽑는다.
    2. 해당 bounding box를 같은 크기로 바꾼 뒤, CNN(여기서는 AlexNet)을 통하여 feature를 뽑는다.
    3. features를 SVM(support vector machine)을 통하여 classification한다.
    • 1번의 물체를 추정되는 부분의 bounding box를 전부 뽑는 부분이 엄청나게 느리다.

    SPPNet

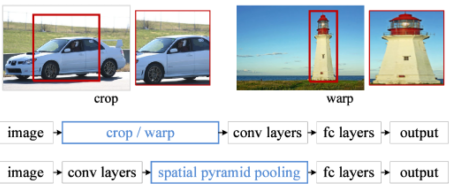
    [img. SPPNet의 구조]

    • CNN을 한번만 돌린 뒤, 해당 바운딩 박스 하나에서 feature를 뽑고 나서 그것을 spatial pyramid pooling을 통하여 classification함.

    Fast R-CNN

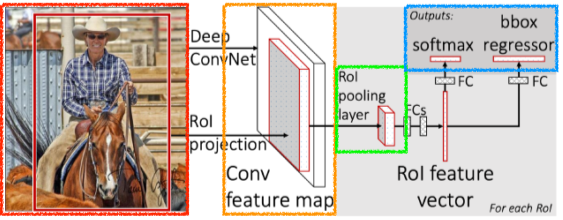
    [img. fasc R-CNN]

    • SPPNet과 비슷하다.
    1. 인풋 이미지의 바운딩 박스를 여러개 뽑는다.
    2. CNN feature map을 만든다.
    3. ROI(region of interest) pooling을 통하여 feature map을 뽑고, classification과 bounding-box regressor를 뽑는다.

    Faster R-CNN

    • Fast R-CNN + Region Proposal Network

    • Region Proposal Network(RPN)

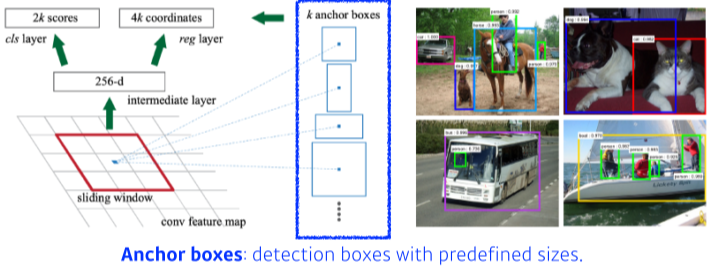
    • [img. RPN 예시]

      • 바운딩 박스를 찾는 알고리즘 또한 교육함, classification은 하지 않음.
      • Anchor Boxes: 미리 정의한 물체 크기로 이루어진 kernel

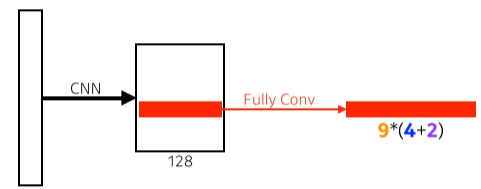
    • [img. RPN 차원]

      • RPN의 Fully Conv에 의해 해당 공간이 원하는 물체를 가지고 있는지 판단
      • 3개의 region 크기(128, 256,512)와 3개의 비율(1:1, 1:2, 2:1)을 가진 총 9개의 anchor boxes를 가짐
      • 각 bouding box가 조정되어야할 크기 (width 크기, height 크기, x offset, y offest) 4개
      • 해당 bounding box가 classification에 쓸모 있는가?(use it or not) 2개
      • 총 9*(4+2) = 54개의 채널을 가진 Fully Conv를 가진다.

    • 좀 더 좋은 성능의 detection 가능

    YOLO(You only look once)

    [img. yolo 예시]

    • v5 까지 나왔음, 아주 빠름, 리얼 타임을 유지할 수 있다.

    • 추출한 bounding box들의 feature를 통해 각각 classification 하는 방식이 아니라, 한꺼번에 모든 bounding box를 classification 함

    • 여러 bounding box를 동시에 한번만 하므로 YOLO라고 한다.

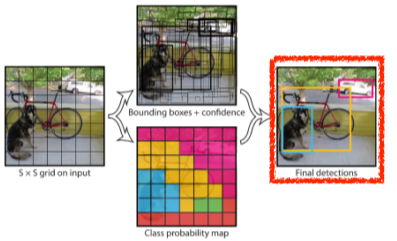
      [img. YOLO 절차]

      1. 먼저 주어진 이미지를 SxS 그리드로 나눈다.
        • 찾고 싶은 물체의 중앙점이 속해있는 그리드에서 bouding box와 classification을 진행한다.
      2. 무언가 물체의 중앙점을 갖는 여러개의 bounding box의 x,y 위치와 w,h 크기 그리고 쓸모 여부를 예측한다 ( 이 정보 5개를 B 라고 하자.).
      3. 위 2번과 동시에 각 그리드가 속한 물체의 classification(C개의 class가 있다고 가정하자)을 진행한다.
      4. 해당 정보를 취합한 뒤, SxSx(B*5+C) 사이즈를 가진 tensor가 된다.

    • v2의 경우 ROI 처럼 미리 정의된 크기의 bounding box를 이용하기도 하고, 다른 모델들 또한 yolo의 방법을 사용하는 등의 상호의 장점을 이용한 발전을 한다.

    Sequential Models - RNN

    Sequential Model

    • sequential data란 순서 관계가 중요한 연속형 데이터로, 입력의 차원의 크기를 정확히 알 수 없다는 문제가 있다.(언제 부터 언제까지의 데이터를 사용해야하는가? 언제 데이터는 끝이 나는가?)
    • 이러한 문제 때문에 CNN이나 Fully connected layer는 사용 못한다.
    1. Naive sequence Model

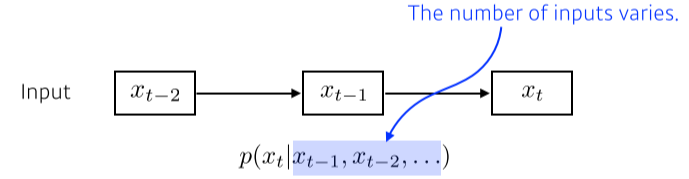
    [img. Naive sequence Model]

    • 과거의 정보들을 모두 고려하는 모델
    1. Autoregressive model(AR model)

    [img. Autoregressive model]

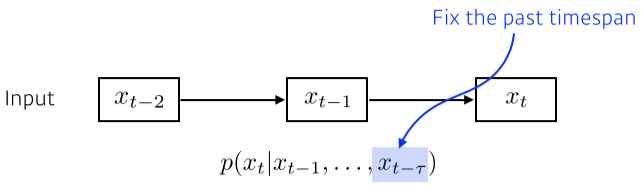
    • fixed timespan $\tau$만큼 만을 고려하는 모델
    1. Markov model(first-order autoregressive model)

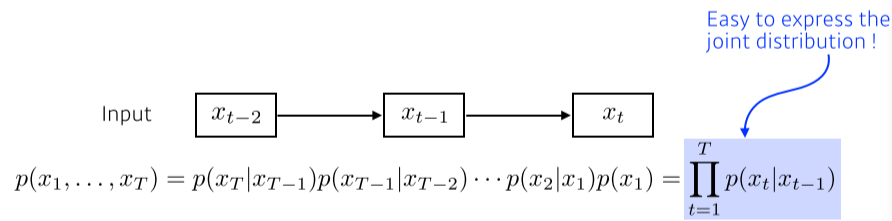
    [img. Markov model]

    • 바로 전 정보만을 이용하는 모델, joint distribution 표현이 쉬움
    1. Latent autoregressive model


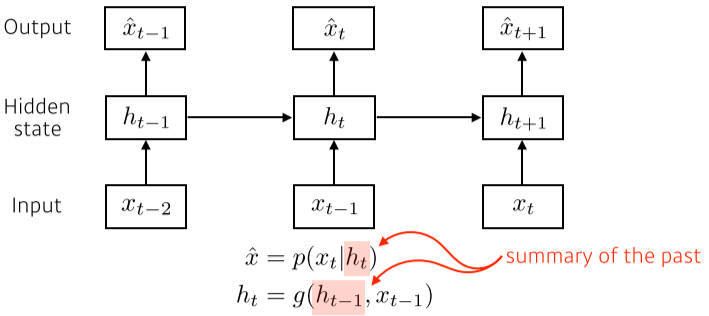
    [img. Latent autoregressive model]

    • 중간의 과거 정보들을 요약하는 Hidden state를 생성하여 해당 정보를 이용하는 모델

    Recurrent Neural Network(RNN)

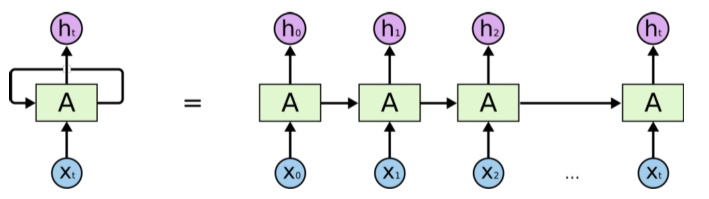
    [img. RNN 그림]

    • RNN은 AR model들을 구현한 신경망,
    • Short-term dependecies : RNN의 단점, 과거 시점의 정보가 미래에 영향을 끼치기 힘듦, 이를 해결하기 위해 밑의 LSTM이 나타남.

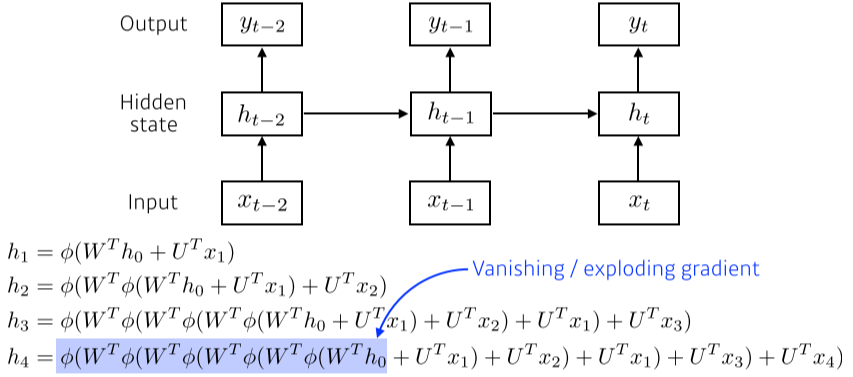
    [img. RNN hidden state의 gradient 문제의 원인]

    • 또한 Activation function의 종류에 따라 Vanishing/exploding gradient 문제가 생길 수 있다.
      • RNN에서 ReLU를 잘 안쓰는 이유

    Long Short Term Memory(LSTM)

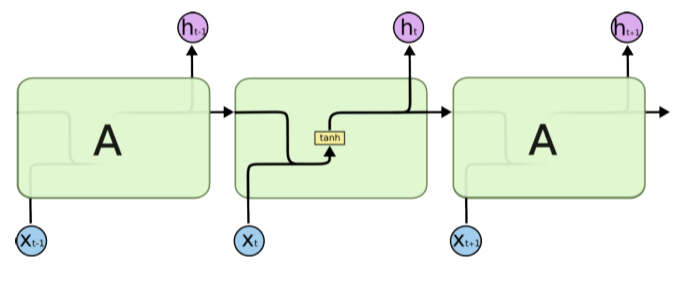
    [img. Vanilla RNN Unit]

    • tanh(hyperparabolic) 함수를 activation 함수로 활용하는 기본 유닛이다.

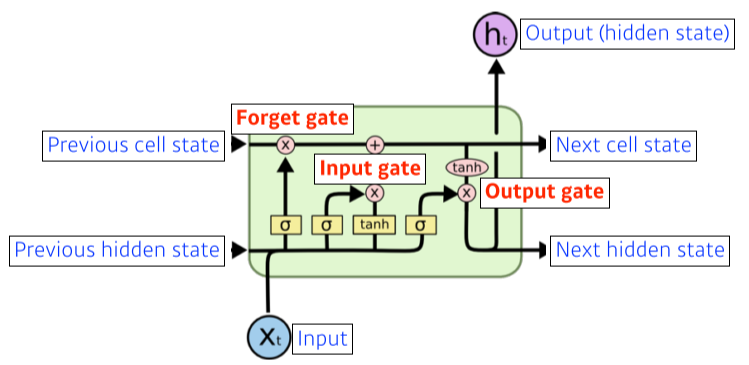
    [img. LSTM Unit]

    • Long Term dependency 문제를 해결하는데 좋은 LSTM 유닛
    • 이전 LSTM Unit에서 이후 LSTM Unit으로 cell state와 hidden state 를 넘겨주게 된다.
    • cell state는 hidden state와 달리 output으로 나오지 않으며, 일종의 이전 정보들을 summary를 해주는 정보, LSTM의 Core idea

    Gate

    • LSTM을 이루는 3개의 게이트가 존재, LSTM의 데이터를 조작
    1. Forget Gate

    [img. Forget gate 구조]

    • 어떤 정보를 잊어버릴지 결정.
    • f~t~는 sigmoid를 사용하여 0 에서 1 사이 값으로 나오며, 이전 cell state 정보의 일부를 버리거나 살린다.
    1. Input Gate

    [img. Input Gate 구조]

    • 어떤 정보를 cell state에 올릴지 결정
    • i~t~는 이전 Hidden state와 X~t~를 통하여 어떤 정보를 올릴지 말지 결정한 결과인 i~t~를 만든다.
    • 또 한 마찬가지로 이전 Hidden state와 X~t~를 통하여 올릴 정보인 $C_t^{\sim}$(C 틸다)를 만든다.

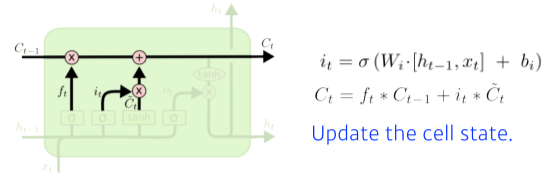
    [img. 새로 통과시킬 Cell State 형성]

    • $C_t^{\sim}$와 i~t~,f~t~ 를 이용해 업데이트할 Cell을 만들게 된다.
    1. Ouput Gate

    [img. Oupt Gate 구조]

    • 위에서 만든 Update cell state와 input 을 이용해 output값을 만든다.

    Gated Recurrent Unit(GRU)

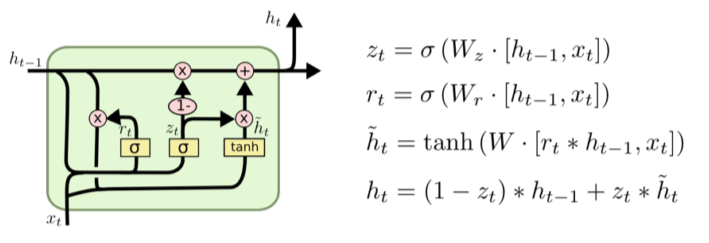
    [img. GRU unit 구조]

    • reset gate와 update gate만 존재하며 cell state가 존재 하지 않다.
      • forget gate와 비슷한 reset gate와 비슷한 update gate가 존재한다.
    • LSTM에 비해 구조가 단순하여 parameter 수가 적어 generalization performance가 좋으며, 성능이 좋은 편이다
    • 하지만 최근에는 위 세가지 구조 전부를 transfromer 구조로 대체되는 추세이다.

    Transformer 모델

    • Jay Alammar의 블로그에서 가져온 그림들임(http://jalammar.github.io/illustrated-transformer/)

    • 불규칙적이고 예상하기 힘든 sequential 데이터의 문제점을 해결한 모델

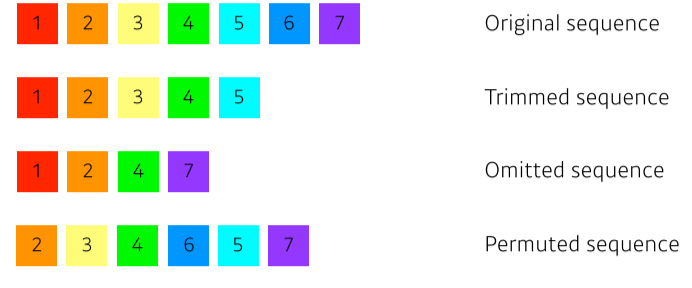
    [img. sequential data의 대표 오류]

    Transformer

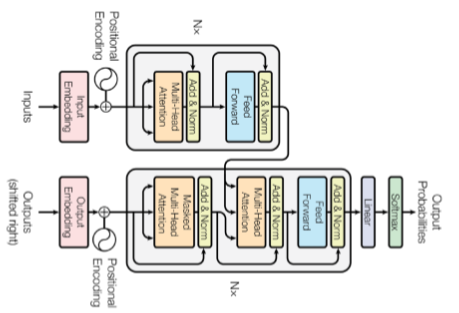
    [img. Transformer 모델 예시]

    • 재귀적 구조가 없는 대신, attention이란 구조를 활용한 sequence model

    • 기계어 번역 문제를 해결하기 위해 시작했지만 여러 문제를 해결 할 수 있다.

    • Encoder와 Decoder 구조로 이루어져 잇다.

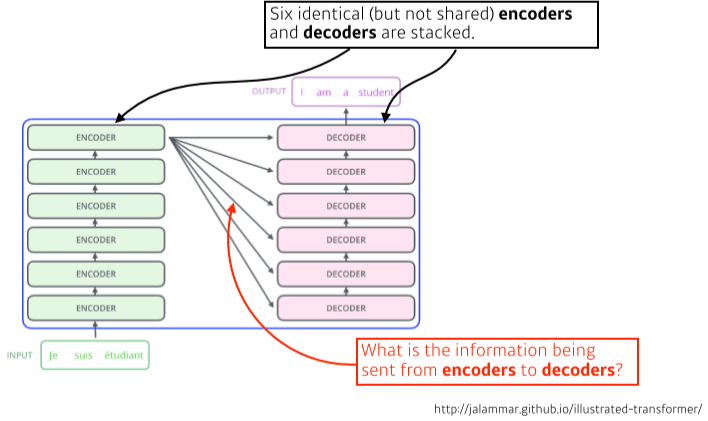
    [img. NMT 문제에서 encoder, decoder 구조]

    • 동일한 구조, 다른 파라미터를 받는 encoder, decoder가 쌓여있는 구조
    • 하나의 모델에 입력과 출력 값이 각각 도메인, 입력의 숫자 등을 다르게 줄 수 있다.
    • 즉 encoder-decoder 모델의 경우, encoder가 하나씩이 아닌 한번에 입력을 처리한다.

    어떻게 encoder는 한번에 n개의 입력을 동시에 처리하는가?

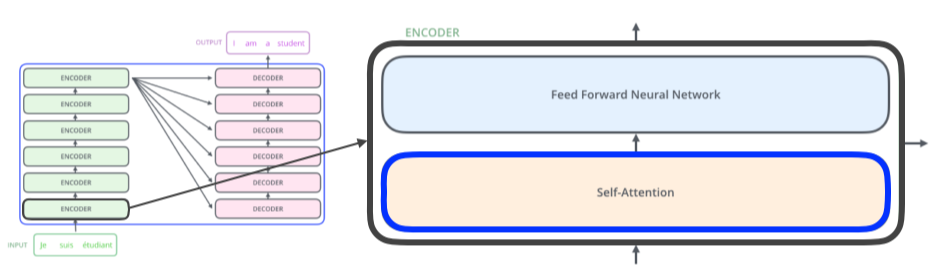
    [img. encoder 구조]

    • Feed Forward Neural Network: MLP때와 동일

    • Self-Attention: encoder와 decorder 구조의 핵심, Attention이란 해당 단어를 처리할 때 다른 단어에 얼마나 관계성을 할당하는 가?이다.

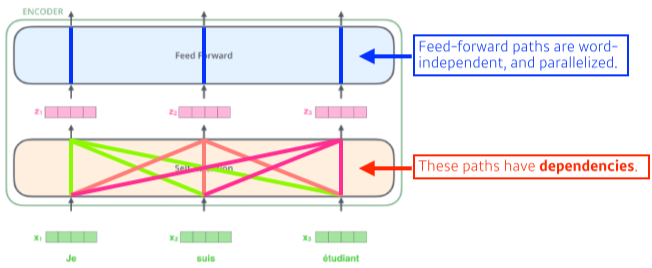
    [img. 단계1, 2 ]

    1. 먼저 각 단어들을 embedding vector로 바꾼 뒤, self attention 층에서 입력된 n개의 단어들을 모두 고려하여 새로운 z벡터를 생성한다.
    2. 그 후 Feed Forward에서는 동일한 조건의 Feed-forward 층을 각 단어 독립적으로 통과 시킨다.
    좀 더 자세한 벡터 처리 예시

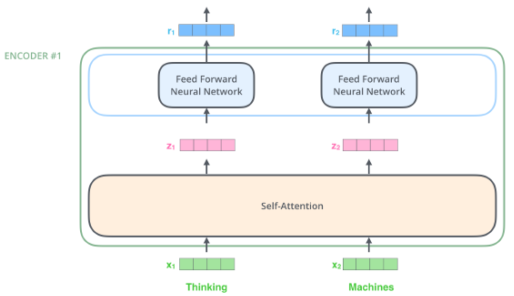
    [img. 단어가 2개 주어졌을 시 예시]

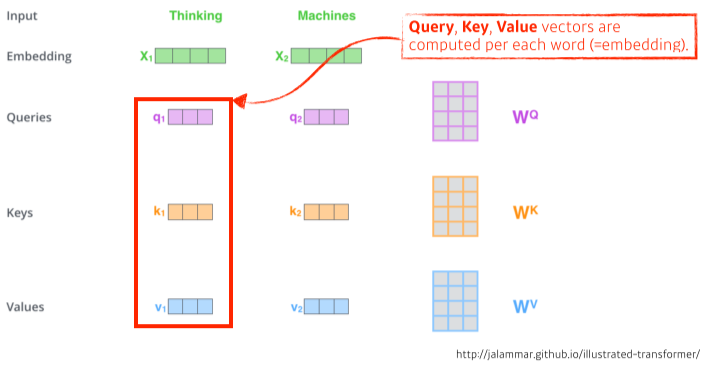
    [img. 세 벡터 생성]

    • Self attention 구조는 embedding된 벡터 형태로 단어가 주어지면, 각 단어 마다 Neutral network를 이용해 Queries, Keys, Values 라는 세개의 벡터(Q,K,V 벡터)를 생성한다.
      • 이 세 벡터를 통해 embedding vector를 새로운 벡터로 바꿔준다.(=encoding)

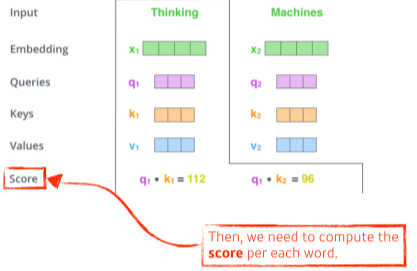
    [img. Thinking 단어의 Score 생성]

    • Thinking의 Queries 벡터와 모든 단어들의 Keys 벡터를 내적(inner product)하여 Score를 생성
      • Score를 통해 다른 단어와의 관계성, 유사성 등(=attention)을 구할 수 있다.

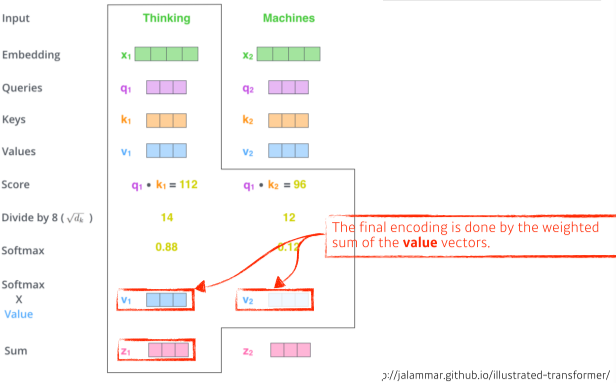
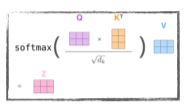
    [img. Score의 normalize 및 z1 벡터 생성]

    • Score 값을 8(키 벡터의 차원(여기서는 64)의 루트,$\sqrt d_k$)로 나눠 주어 Normalize(일정 범위에만 머무르게 하기 위해서)한다.
    • 이 후, softmax 함수로 0~1 사이로 만들어 Attention weights를 만든다.
    • Attention Weights를 Value vector로 Weighted Sum을 하여 한 단어의 z(인코딩 벡터) 벡터를 생성한다.

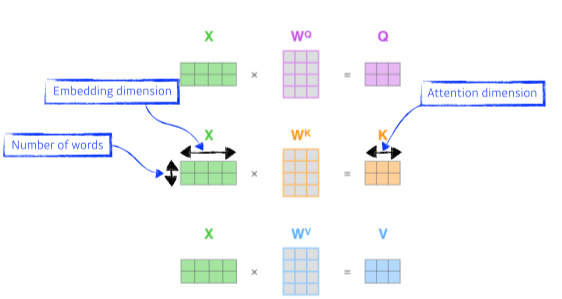
    [img. Key, Query, Value vector 생성]

    • W^Q^,W^K^,W^V^는 모든 단어가 공유한다.

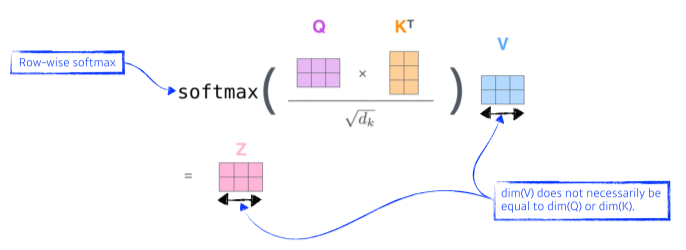
    [img. 인코딩 벡터 생성]

    • Value vector의 차원은 엄밀히 말해 weighted sum만 하므로 Query vector, Key vector와 달라도 된다.

    Transformer 구조의 장단점

    • 이런식으로 모든 단어들이 서로 영향을 주므로, 같은 단어라도 다른 단어가 들어가면 결과값이 달라지므로, 변화에 용이한 모델이 나온다..
    • 대신 모든 단어를 고려해야하므로 많은 컴퓨팅 자원이 필요하다.

    Multi-headed attention(MHA)

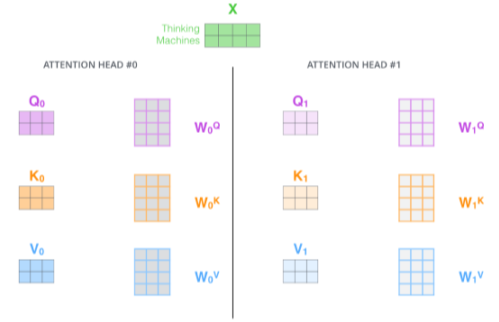
    [img. attention이 2번 실행된 단어]

    • attention 과정을 여러번 실행함, 단어마다 Query, Key, Value 벡터가 여러개 생성된다.

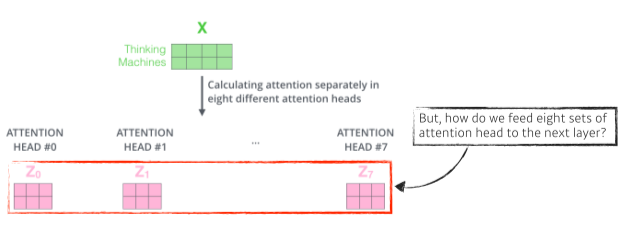
    [img. 여럿 생성된 인코딩 벡터]

    • 이를 통해 여러개(예시에선 8개)의 인코딩 벡터(z0~z7)를 생성하게 된다
    • 이 8개를 합쳐서 다음 layer에 input 되어야 한다.

    [img. learnable linear map을 통해 통합된 차원의 벡터(Z)로 생성]

    • input된 단어, embedding vector와 output 인코딩 벡터(z)들의 차원이 같아야한다.
    • 그러므로 Learnable Linear amp을 이용해 교육시킨 W^o^값을 곱해서 차원을 맞춰준다.

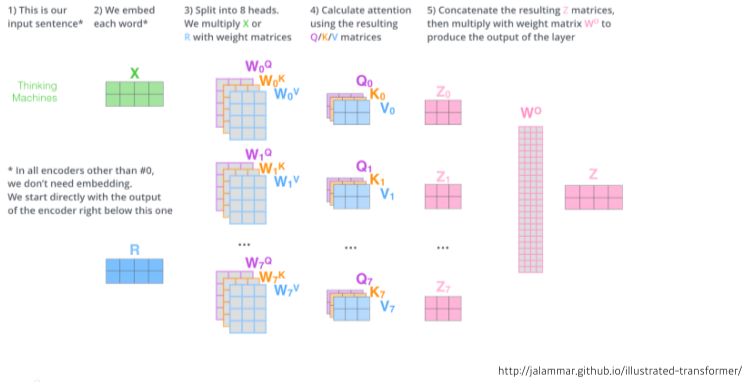
    [img. 전체적인 MHA의 동작]

    • 실제로는 위의 방법보다는 input의 embdding vector를 n개로 나눈 뒤, 나눠진 일부들로 attention을 만든 뒤, 다시 concatenate 한다.
      • ex) 100차원 input -> 10개로 나누어 10차원 z0~z10 10개 생성 -> 100차원 output
        (Z)으로 합침

    1. (위의 n개의 동시 처리 예제에서 output을 구한 뒤 부터 이어짐) attention을 하기 이전에 embedding vector에 POSITIONAL ENCODDING 이라는 벡터를 더해준다.

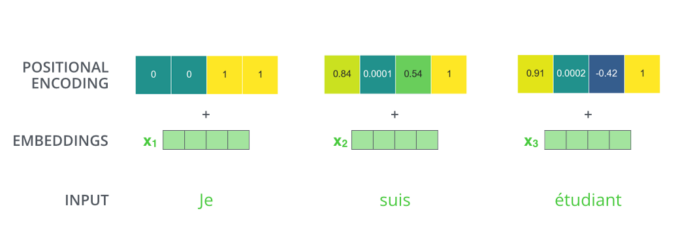
      [img. positional encdoding의 합]

      • 일종의 bias와 비슷하며, 위 attention 과정을 보면 data의 sequence와 independent 하기 때문에(즉, 단어의 순서가 뒤바껴도 같은 값이 나오게 되어있다.) 이를 방지하기 위해 더해준다.

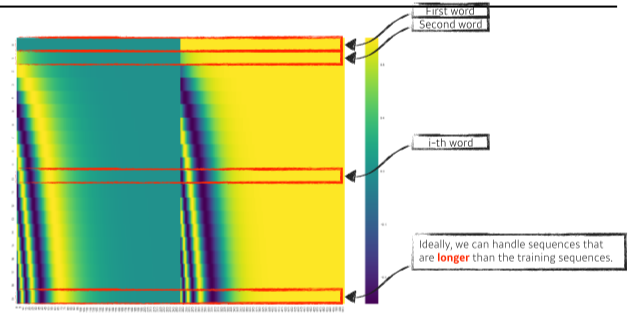
    [img. 512-dimensional 일시, positioinal encoding 벡터 구하는 법1]

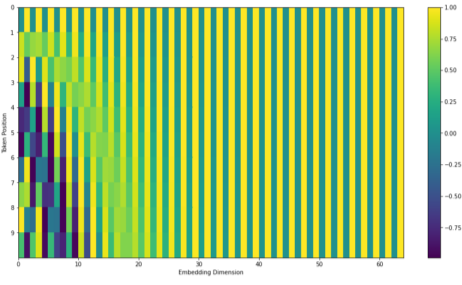
    [img. 최신 방법의 Positional encoding 구하는 법 2]

    • 포지션별로 특정 그래프의 값을 가져와 더해주면 된다.(predefined)

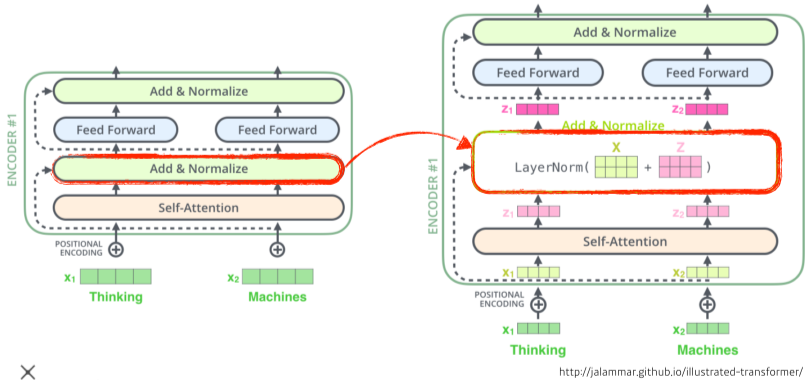
    [전체적인 encoder의 과정]

    decoder와 encoder 사이에는 어떤 정보가 교환되는가?

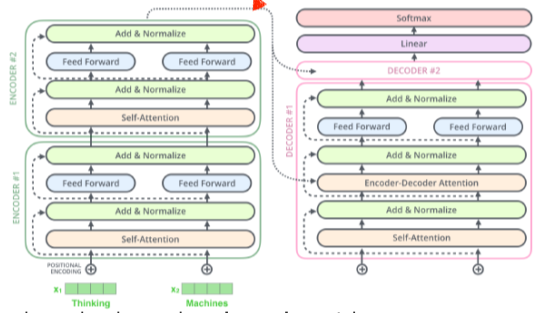
    [img. encoder와 decoder 사이의 정보교환 그림]

    • decoder에서는 주어진 vector로 유의미한 결과를 만드는 역할을 한다.

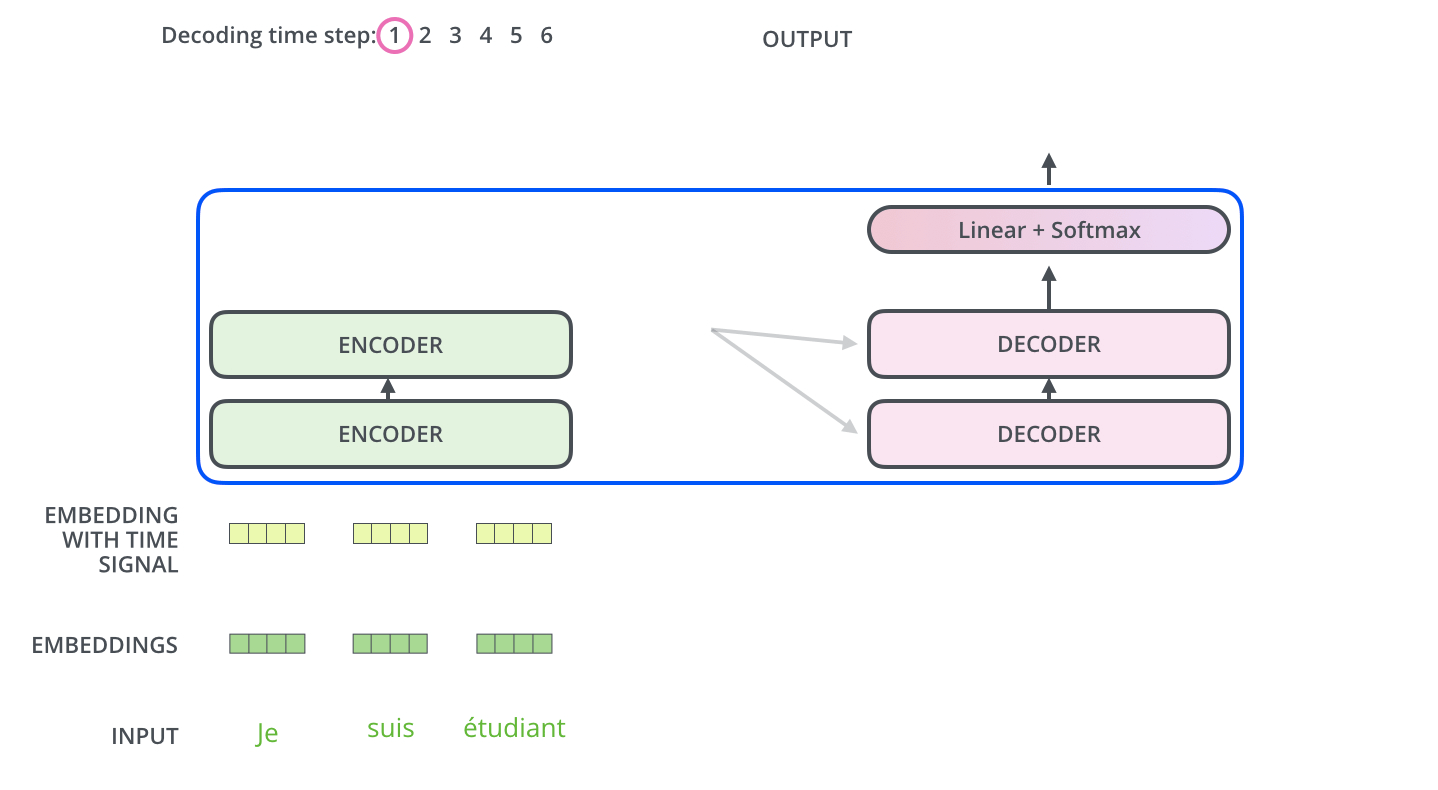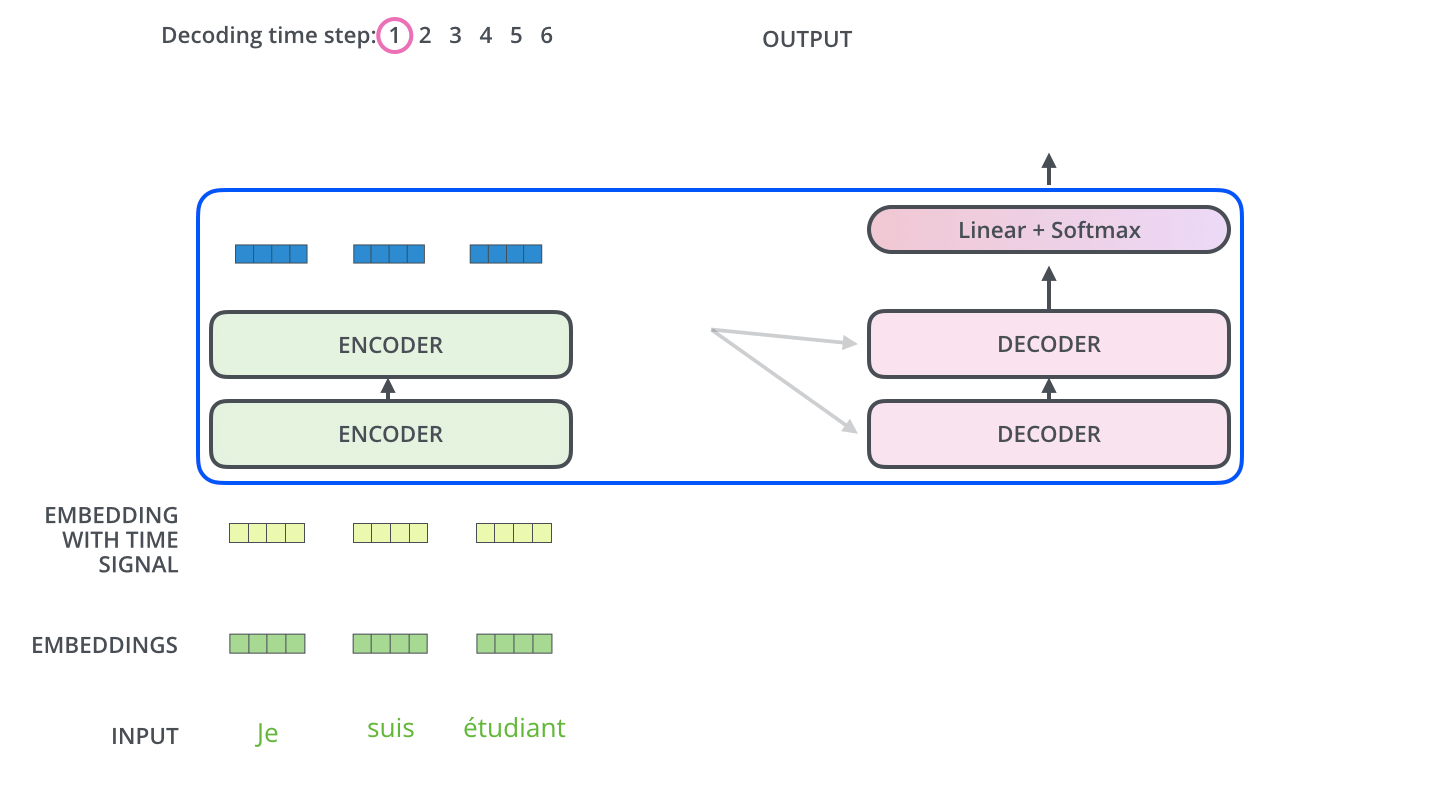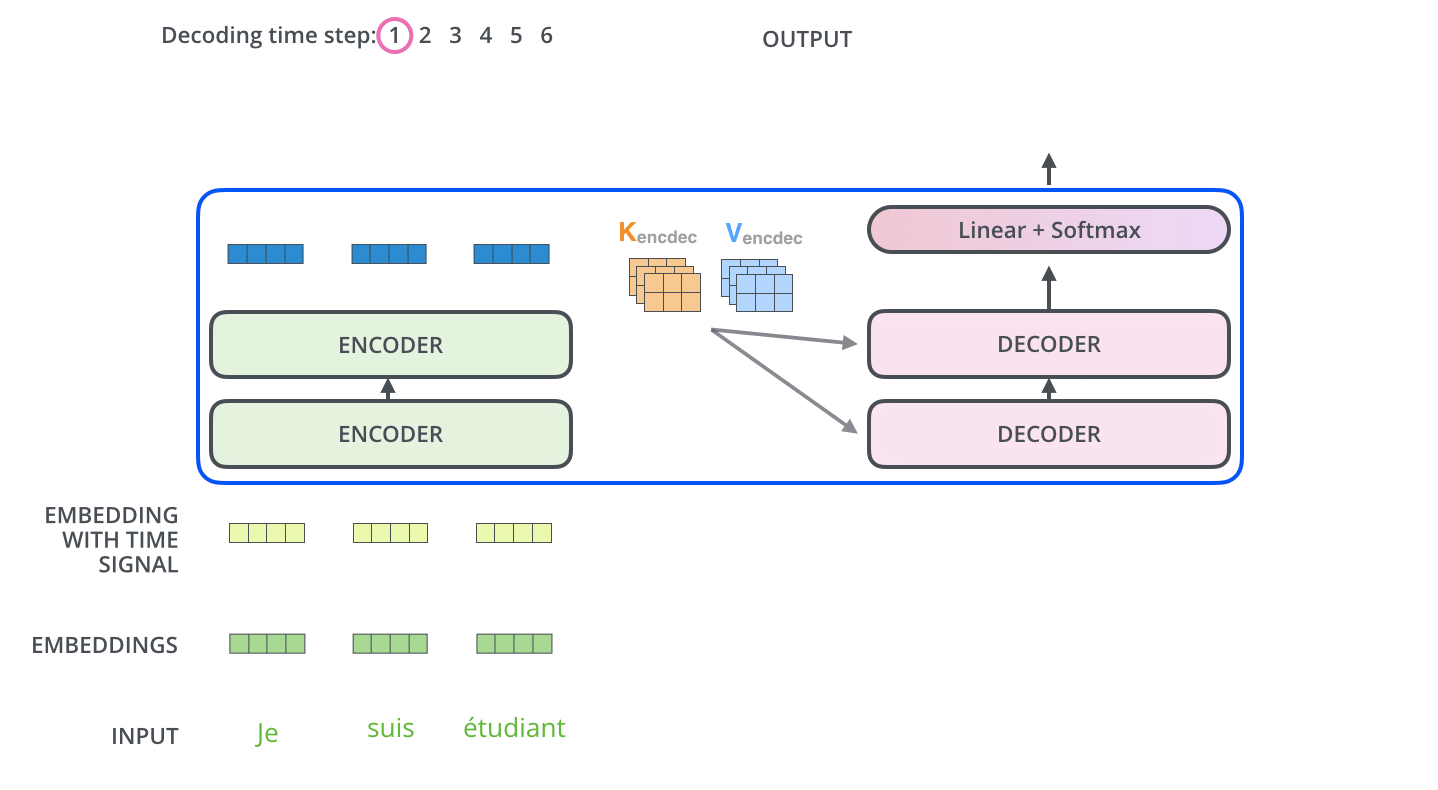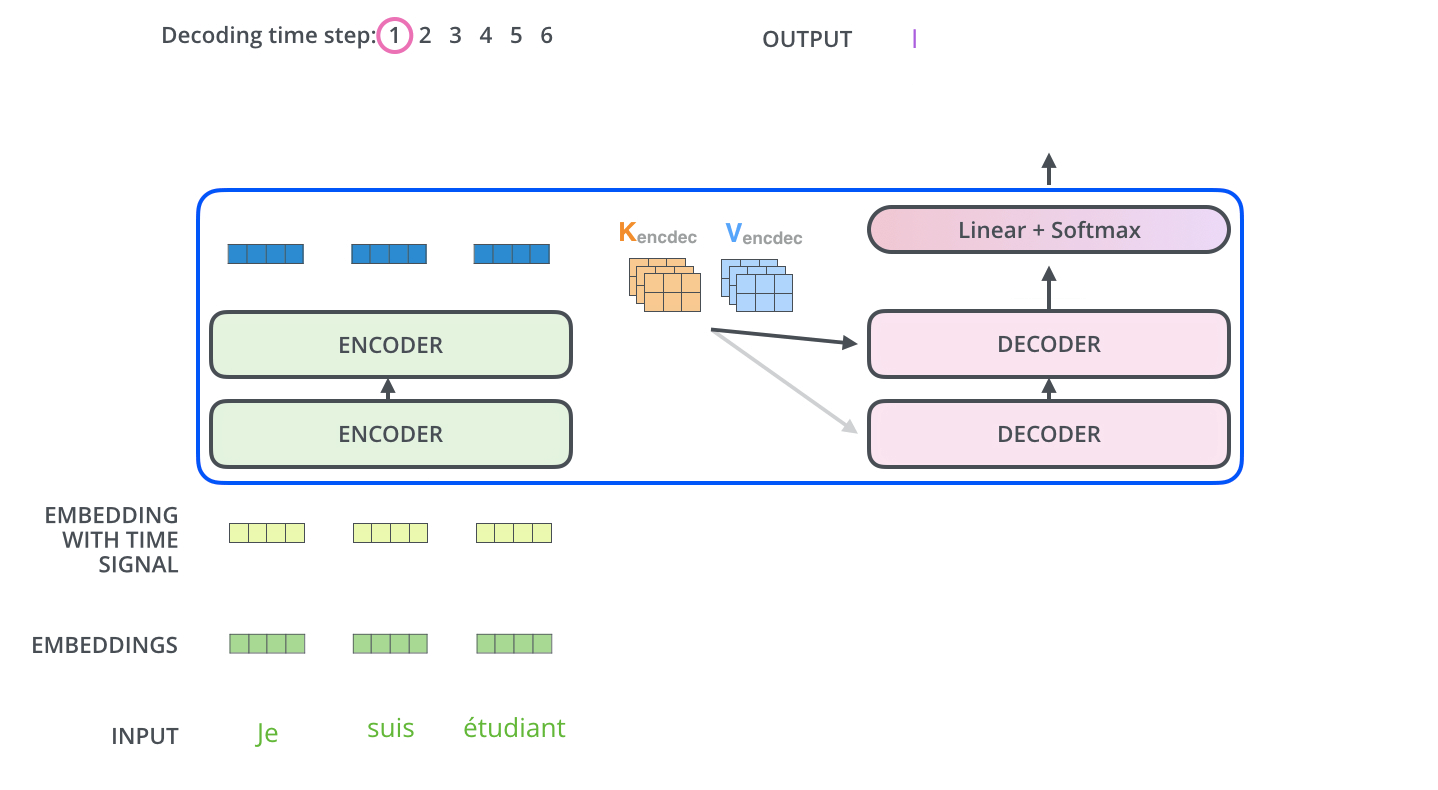
    [gif. encoder decoder 통신 애니메이션1]

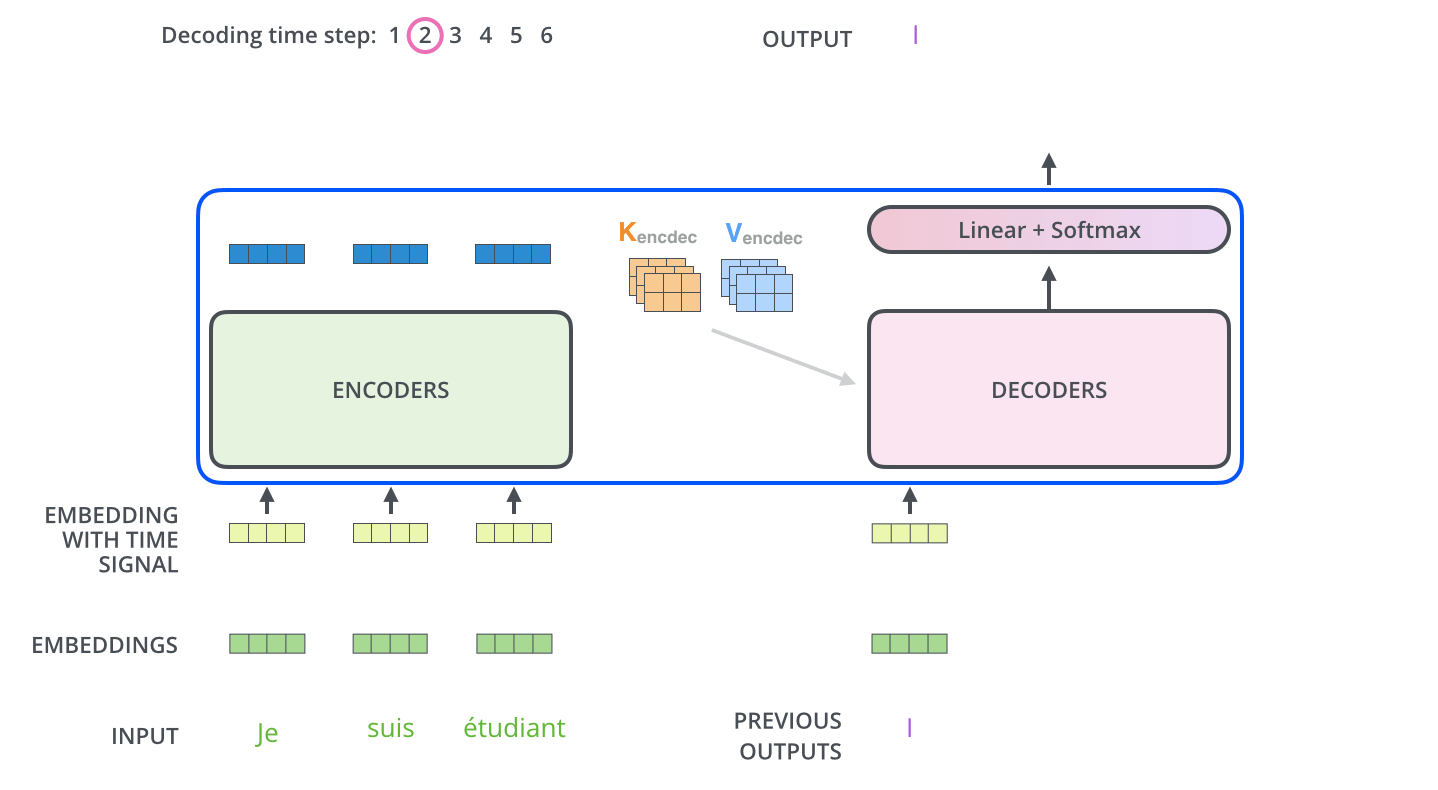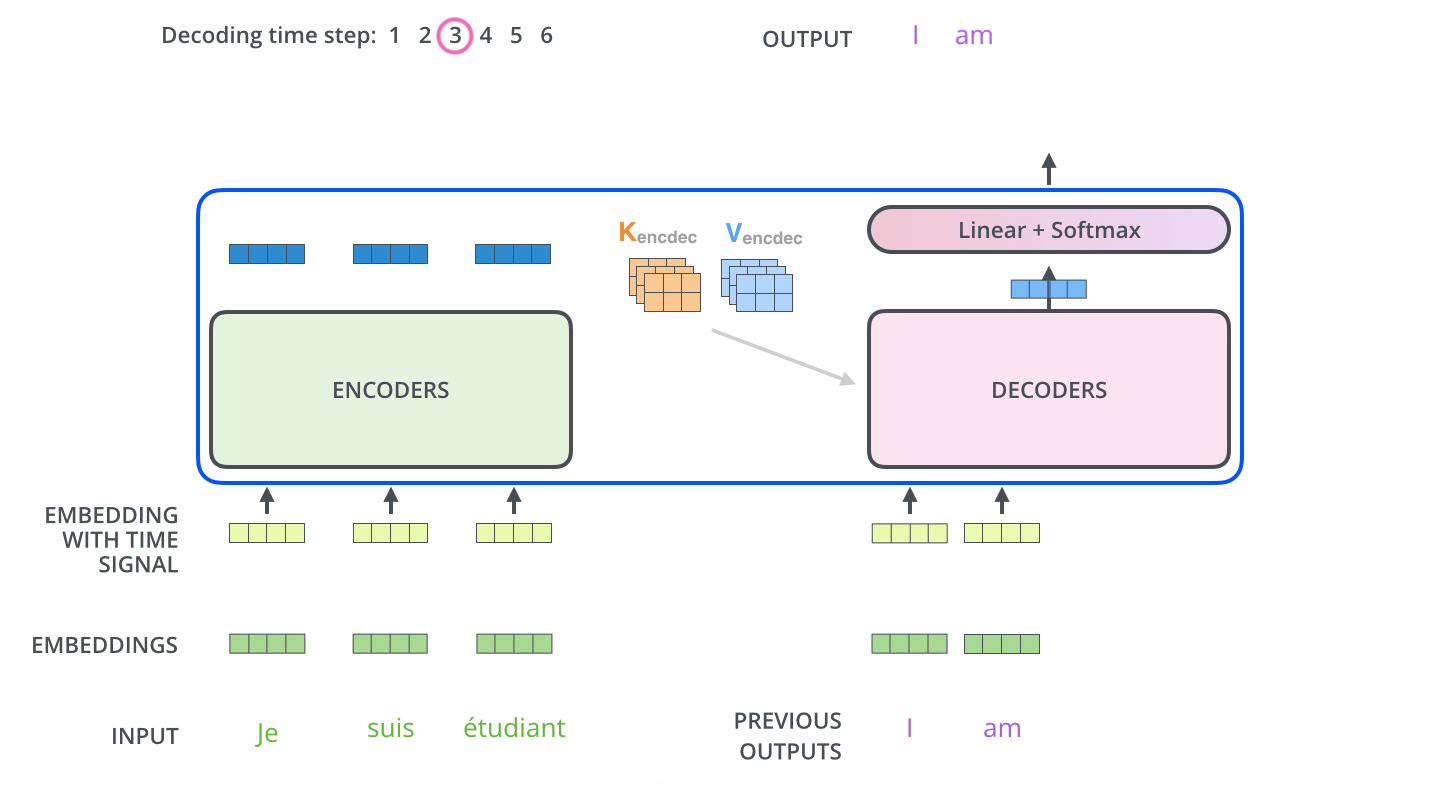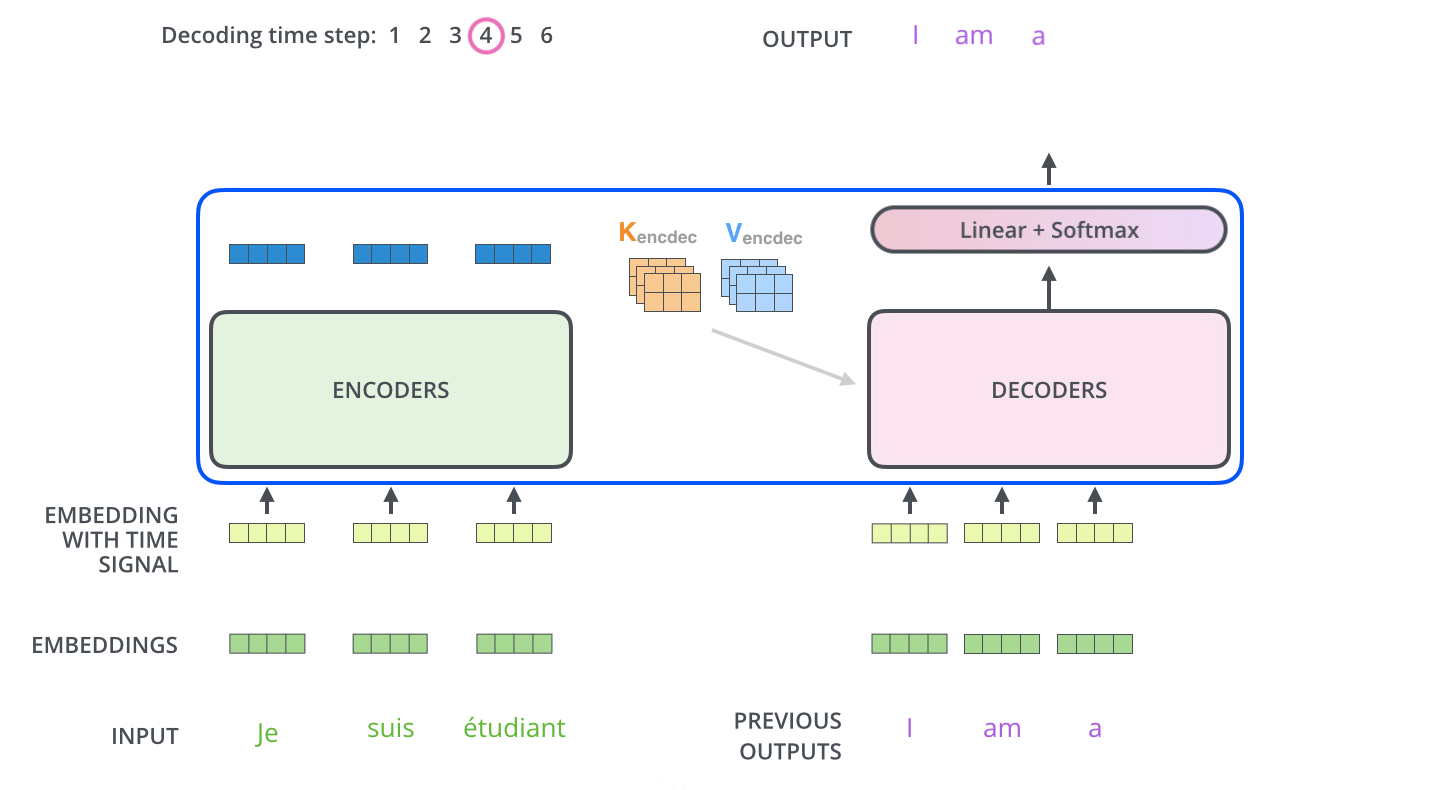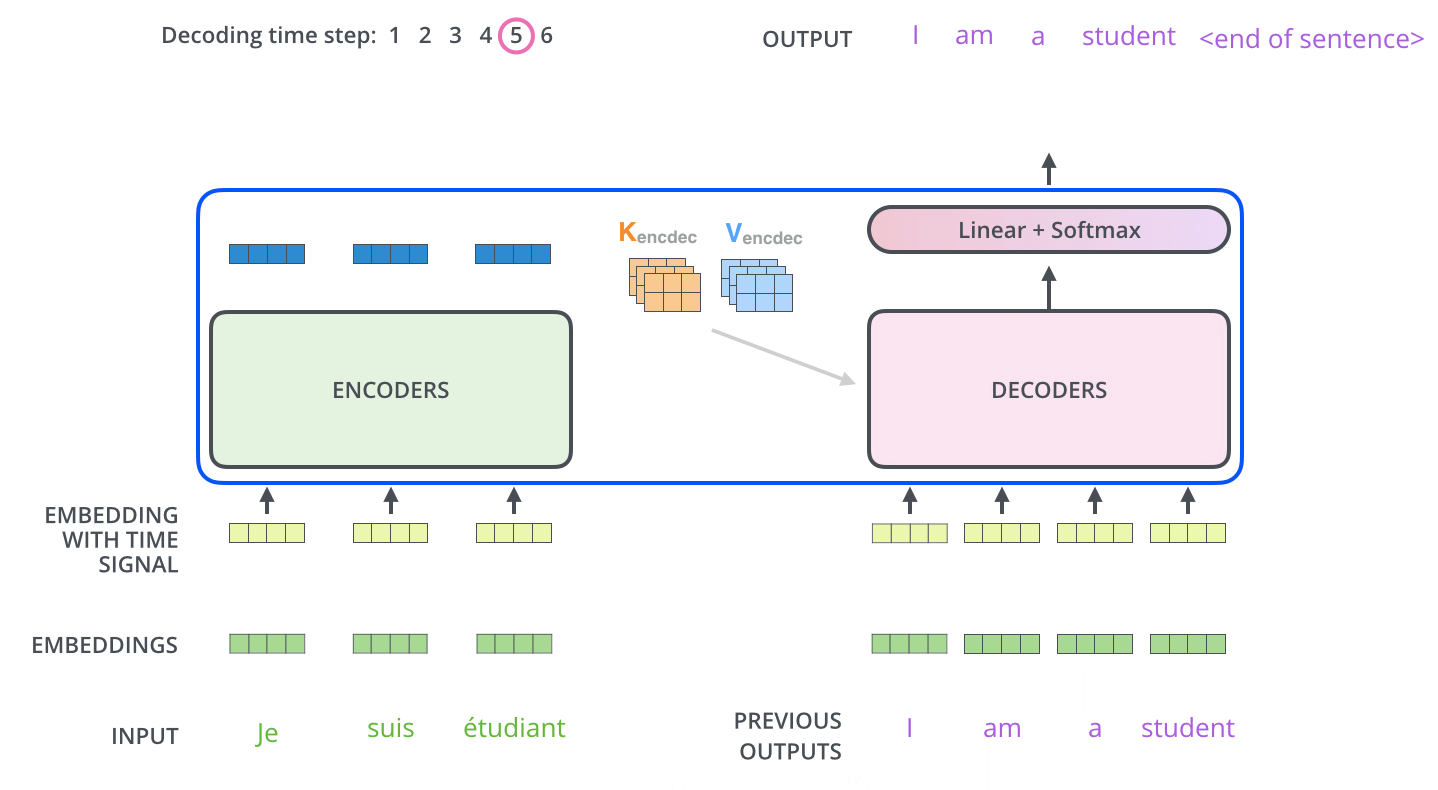
    [gif. encoder decoder 통신 애니메이션2]

    • 가장 상위 layer의 encoder의 결과값(z) 벡터의 key와 value, 두 벡터를 decoder layer들로 보낸다.

    decoder는 어떻게 결과값을 만들어 내는가?

    • 이후 decoder에 들어가는 Query vector와 k, v 벡터로 auto regressive 하게 결과물을 출력한다.

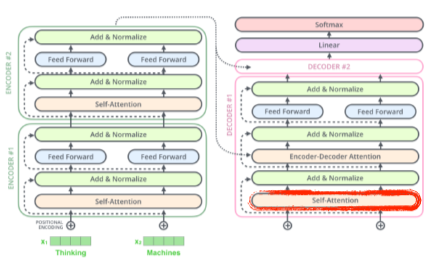
    [img. decoder 학습 과정]

    • 이후, decoder의 slef-attention layer에서 masking을 통하여 생성하려는 단어와 그 뒤 생성해야할 단어들을 가린 뒤, 앞에서 이미 생성한 단어에 의존해서 학습하게 만든다.
    • 또, Encoder-Decoder attention layer에서 encoder에서 준 벡터 둘을 받아서 학습시킨다.

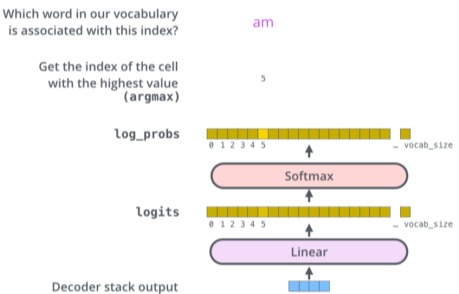
    [img. decoder 학습의 최종 과정]

    • 마지막 층에서는 단어들의 배열에서 단어를 샘플링해서 결과 값을 낸다.

    Transform 모델의 근황

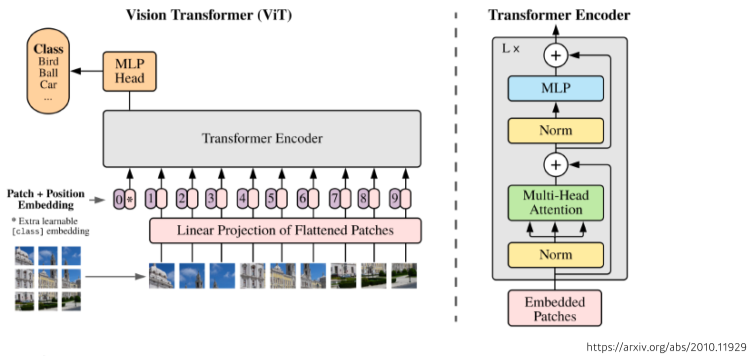
    [img. encoder만 활용하여 이미지 class 구분하는 모델]

    • 단순히 단어나 다른 sequential data 뿐만아니라 vision 영역에도 활용되고 있다.
    • openAI의 DALL-E에서 문장을 통해 이미지를 생성하는 연구 또한 Transformer의 decoder를 활용하여 진행했다.

    Generative Models(생성 모델)

    Introduction

    • Generative Model이란, 이미지 등을 생성하거나, 확률 밀도를 탐색하거나 비지도 특색 학습에 사용되는 모델을 의미한다.
      • Generation: 이미지 생성 등(sampling)
      • Density estimation: 이미지가 강아지 같은가? 고양이 같은가? (anomaly detection), classify 모델을 포함하고 있음. (explicit 모델, <=> inplicit model: 생성 위주가 가능한 모델)
      • Unsupervised representation learning: 이미지 내부의 특색 탐색 (feature learning)

    Basic Discrete Distributions

    1. Bernoulli distribution : 동전 던지기 처럼 0 또는 1이 나오는 형태
      • $D={Heads, Tails}$
      • Specify P(X = Heads)=p. Then P(X=Tails) = 1-p.
        • 예를 들어 앞면이 p 면 뒷면이 나올 확률은 1-p다.
      • Write: X ~ Ber(p).
    2. Categorical distribution: 주사위 던지기 같이 구분되는(discrete) 여러 결과값이 나오는 형태(1~6)
    • $D={1,\dots,m}$
    • Specify P(Y = i) = pi, such that $\sum^m_{i=1}p_i=1$.
      • 모든 확률을 합해서 1
    • Write: Y ~ Cat(p~1~, …, p~m~)
    1. 예시
    • RGB pixel이 가지는 경우의 수는 256 * 256 *256이며, 필요한 파라미터의 수는 255*255*255.

    Structure Through Independence & Conditional Independence

    • binary pixel의 수가 100개 라고하면 가능한 파라미터는 2^100^-1개가 되고, 이는 너무 많다.

    • 만약 모든 Pixel이 서로 independent 한다고 가정하면 경우의 수는 같지만, 파라미터의 수는 n(=100)개로 줄일 수 있다.

    • 하지만 실제로 independent 하지 않으므로 너무 말이 안되는 가정이다.
    • 이 둘 사이의 타협점을 찾기위한 것이 Conditional independence 이다.
    \[Chain\ Rule:\ p(x_1,\dots,x_n)=p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)\dots p(x_n|x_1,\dots,x_{n-1})\\ Bayes'\ rule:\ p(x|y)=\frac {p(x,y)}{p(y)}=\frac {p(y|x)p(x)}{p(y)}\\ Conditional\ independence:\ if\ x\perp y | z,\ then\ p(x|y,z)=p(x|z)\]

    [math. Conditional independence의 세가지 룰]

    • conditional independence: z가 주워 졌을때, x,y가 independence라고 가정하면 성립, 이를 chain rule과 섞으면 좋은 타협점을 가진 모델을 생성할 수 있다.
    \[Chain\ Rule:\ p(x_1,\dots,x_n)=p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)\dots p(x_n|x_1,\dots,x_{n-1})\\\\ if\ assume\ \ X_{i+1}\perp X_1,\dots,X_{i-1}|X_i (Markov\ assumption)\\ become\ \ \ p(x_1,\dots,x_n) =p(x_1)p(x_2|x_1)p(x_3|x_2)\dots p(x_n|x_{n-1})\]

    [math. chain rule과 conditional indepence의 조합]

    • Markov assumption을 이용하면 parameter 수가 기존의 2^n^-1 에서 2n -1로 변한다.
    • 이러한 conditional indepency 방법으로 생성한 모델을 Auto-regressive model이라고 한다.

    Auto-regressive Model

    • 28 X 28 binary pixel 이미지의 경우 우리는 p(x)를 구하기 위해 autoregressive model로 만들 수 있다.
    • pixel의 order 순서에 따라 모델과 방법론이 달라지기도 한다.(아래 Pixel RNN 참조)
    1. NADE(Neural Autoregressive Density Estimator) 모델

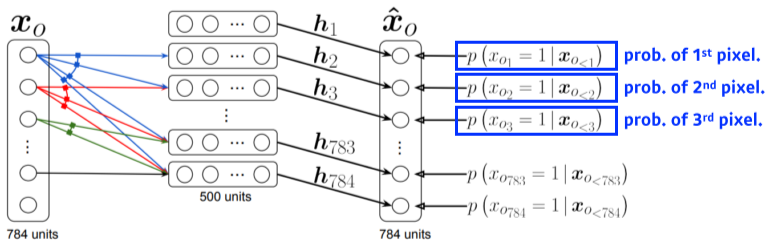
    [img. NADE 모델]

    • i 번째 픽셀을 첫번째 부터 i-1번째 픽셀에 dependent하게 생성(dense layer)
      • 즉, $p(x_i x_{1:i-1}) = \sigma(\alpha_ih_i+b_i)\ where\ h_i=\sigma(W_{<i}x_{1:i-1}+c)$ 이다.
    • 입력 차원이 점점 더 커지게 된다.
    • explicit 모델이며 확률분포를 구할 수 있다.
    \[p(x_1,\dots,x_{784})=p(x_1)p(x_2|x_1)\dots p(x_{784}|x_{1:783}) \\ where\ each\ conditional\ probability\ p(x_i|x_{1:i-1})\ is\ computed\ independently\]

    [math. chaine rule을 통한 joint probability ]

    • 연속적인 분포(continuous random variables)일 경우 a mixture of gaussian을 사용해 표현 가능
    1. Pixel RNN
    • 이미지 내의 pixel 생성하는 auto-regressive 모델
    \[p(x)=\prod^{n^2}_{i=1}p(x_{i,R}|x_{<i})p(x_{i,G}|x_{<i},x_{i,R})p(x_{i,B}|x_{<i},x_{i,R},X_{i,G})\]

    [math.nXn RGB image 생성]

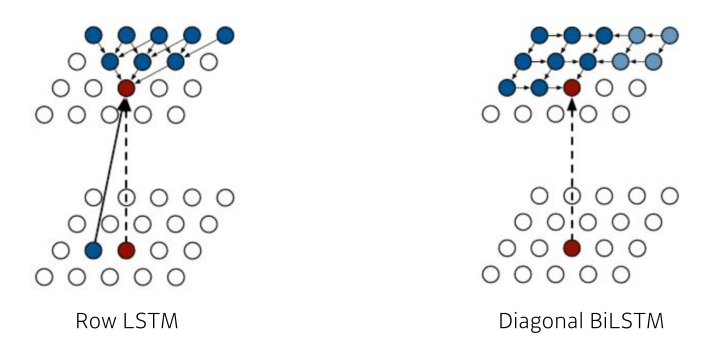
    • ordering에 따라 Row LSTM, Diagonal BiLSTM으로 나눠짐

    [img. 빨간 색이 생성할 pixel, 파란 색이 참조할 pixel이다.]

    Latent Variable Models

    Variational Auto-encoder

    • Variational inference(VI, 변분 추론)

      • VI의 목적은 복잡한 posterior distribution(사후확률 분포)을 variational distribution(변분 분포)으로 최적화하는 것이다.
        • Posterior distribution($p_\theta(z x)$): 관심있는 random variable의 확률 분포, 이것의 반대, $p_\theta(x z)$는 likelihood라고 한다. z는 latent vector를 의미한다.
        • Variational distribution($q_\theta(z x)$): Posterior distribution을 알기 쉽게 근사하는 분포.
      • KL divergence를 loss처럼 이용하여 Variational distribution과 Posterior distribution의 차이를 줄인다.

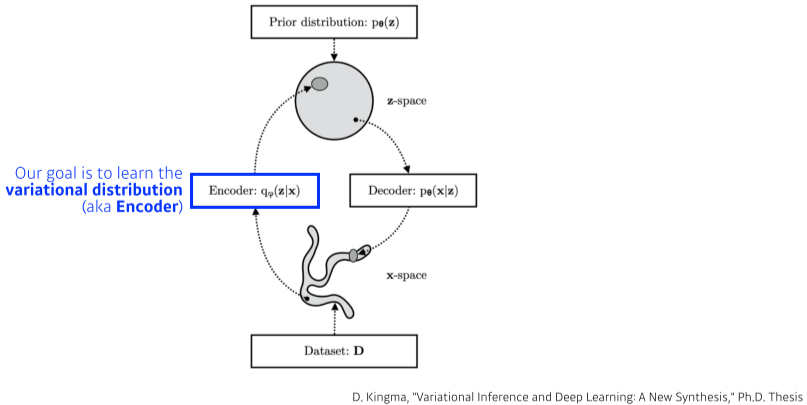
      [img. VI의 그림화]

    • 하지만 우리는 posterior distribution에 근접한 variational distribution을 구하기 이전에, posterior distribution 자체를 모른다.

    • 이를 구하기 위해 ELBO(Evidence lower bound)를 최대로 키우면 반대로 objective 구간은 줄어들게 된다.

      • objective 구간은 KL divegence를 포함하므로 작아질수록 loss가 작아지는 효과와 비슷하다.

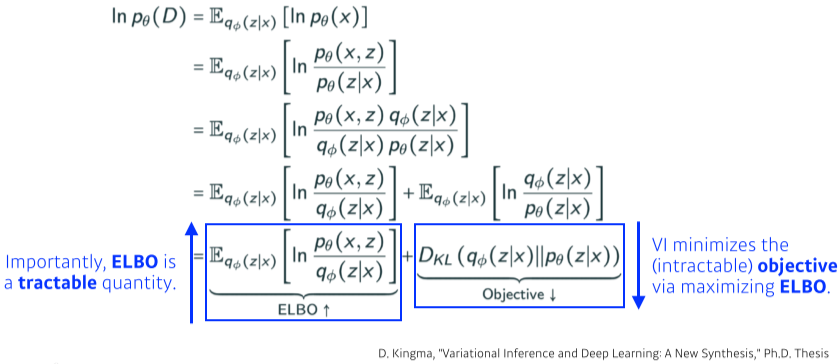
    [img.이 방법을 Sandwitch method라고도 부른다.]

    • Posterio distribution은 알 수 없지만, ELBO는 계산할 수 있다.

    [img. ELBO가 가지고 있는 두개의 텀]

    • ELBO는 두개의 텀을 가지고 있는데, 각각 Reconstruction Term과 Prior Fitting Term로 이루어져 있다.
      • Reconstruction Term : encoder와 latent space를 거쳐 decoder로 돌아오는 reconstruction loss를 줄이는 부분
      • Prior Fitting Term : latent space의 점들의 분포가 Prior distribution(사전 분포)와 비슷하게 만들어 줌
    • 위의 두 텀 때문에 Variational Auto-encoder는 generative model이 된다.
      • 입력 -> latent space -> 분포 찾아서 샘플링-> decoder -> output image 생성
      • 그냥 Auto-encoder에는 존재하지 않으므로 generative model이 아니다.
    • Variational Auto-encoder는 다음과 같은 단점을 가지고 있다.
      • likelihood를 측정하기 힘듬(intractable model)
      • prior fitting term의 KL divergence을 loss 처럼 사용하려면 SGD, Adam 등으로 최적화가 되어야하므로 미분 가능해야 함.
      • 따라서 보통 isotropic Gaussian을 loss funtion에 넣어서 이용함
        • isotropic Gaussian: $D_{KL}(q_\phi(z x)   \mathcal N(0,I))=\frac{1}{2}\sum^D_{i=1}(\sigma^2{z_i}+\mu^2{z_i}-ln(\sigma^2_{z_i})-1)$
        • 모든 output dimension이 independent한 gaussian distribution을 의미함
    Adversarial Auto-encoder(AAE)

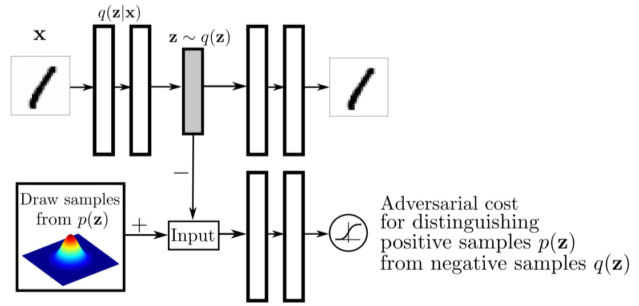
    [img. AAE 구조]

    • KL divergence라는 약점이있는 prior fitting term 대신에 GAN을 활용하여 latent distribution 사이의 분포를 맞춰줌
    • 샘플링 가능한 distribution 이라면 latent prior distribution으로 활용 가능하다.
    • 성능 또한 비교적 좋은 경우가 많다

    Generative Adversarial Network(GAN)

    GAN 소개

    • GAN은 대략 2가지 단계로 이루어져 있는데, 샘플을 생성하는 모델(Generator)과, 샘플을 구별하는 모델(discriminator)로 되어있다.
    • 새로운 샘플을 생성해서 구별 모델에 전달 :arrow_right: 실제 정보와 비교하여 샘플을 구별하여 생성 모델에 전달하고 학습 :arrow_right: 구별한 결과를 학습하여 더 나은 샘플을 생성해서 전달 :arrow_right: 무한 반복
    • 마치 두 모델이 서로 싸우는 형식의 모델이다.

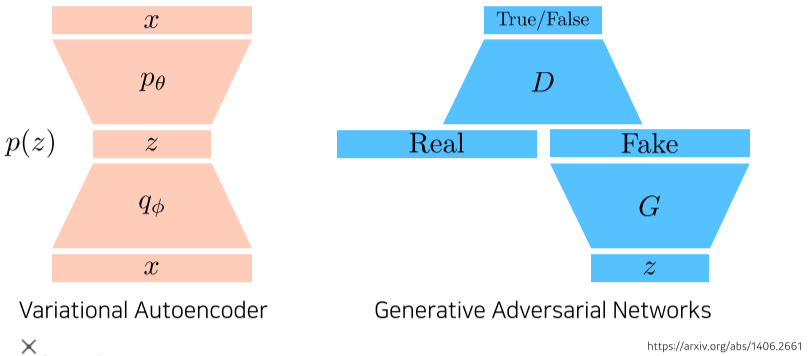
    [img. VA vs GAN 비교]

    • VA의 경우, X의 이미지가 들어오면 인코더, latent vector(z), 디코더를 통과하는 학습을 거친 뒤, generation 단계에서는 p(z)(latent distribution)에서 샘플링한 z를 decoder에 통과시킨 뒤, 그 결과값이 생성된 샘플이다.

    • GAN의 경우, z(latent distribution)을 통해서 Generator에서 Fake 이미지를 만들고, Real 이미지와 Fake 이미지를 Discriminator가 구별,학습해서 그 결과를 Generator에게 보내 학습 시킨다.

    • 이를 수학적으로 표현하면 이와 같다. (implicity 모델이다.)
      • Discriminator 입장
        \(\stackrel {max}{D}\ V(D,G)=\mathbb E_{x\sim p_{data}(x)}[logD(x)] + \mathbb E_{z\sim p_z(z)}[log(1-D(G(z)))]\\ where\ optimal\ discriminator\ is\ D^*_G(x)=\frac{p_{data}(x)}{p_{data}(x)+p_G(x)}\)
      • Generator 입장
      \[\stackrel {min}{G}\ V(D,G)=\mathbb E_{x\sim p_{data}(x)}[logD(x)] + \mathbb E_{z\sim p_z(z)}[log(1-D(G(z)))]\]
      • optimal discriminator(=최적의 discriminator 일시 값) 적용시
      \[V(G,D^*_G(x)) = E_{x\sim p_{data}}\left[log\frac{p_{data}(x)}{p_{data}(x)+p_G(x)}\right]+E_{x\sim p_G}\left[log\frac{p_G(x)}{p_{data}(x)+p_G(x)}\right] \\= E_{x\sim p_{data}}\left[log\frac{p_{data}(x)}{\frac{p_{data}(x)+p_G(x)}{2}}\right]+E_{x\sim p_G}\left[log\frac{p_G(x)}{\frac{p_{data}(x)+p_G(x)}{2}}\right] - log4 \\ = D_{KL}\left[p_{data},\frac{p_{data}+p_G}{2}\right]+D_{KL}\left[P_G,\frac {p_{data}+p_G}{2}\right]-log4\]
      • 여기서,
      \[D_{KL}\left[p_{data},\frac{p_{data}+p_G}{2}\right]+D_{KL}\left[P_G,\frac {p_{data}+p_G}{2}\right] = \\ 2 \times Jenson-Shannon\ Divergence\ (JSD) = 2D_{JSD}[p_{data},p_{G}]\]
      • 이며, 최종적으로
      \[V(G,D^*_G(x)) = 2D_{JSD}[p_{data},p_{G}] - log4\]
      • 이는 이론상 최적의 discrimniator 일시, 최소화 해야할 generator 값이다.

    여러 GAN 모델들

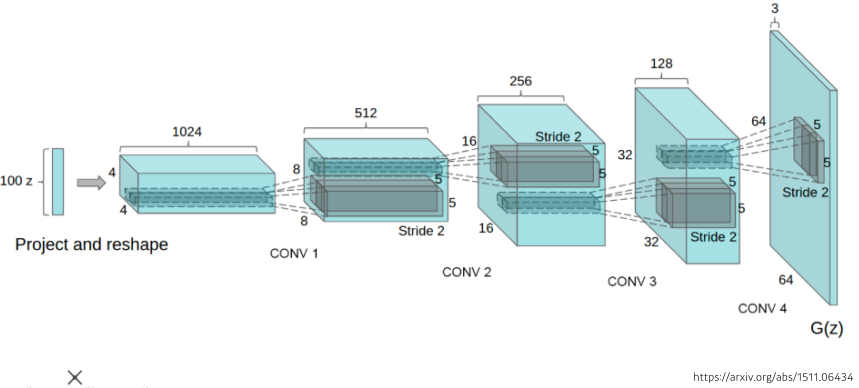
    [img. DCGAN 모델]

    • 이미지 생성하는 GAN 모델

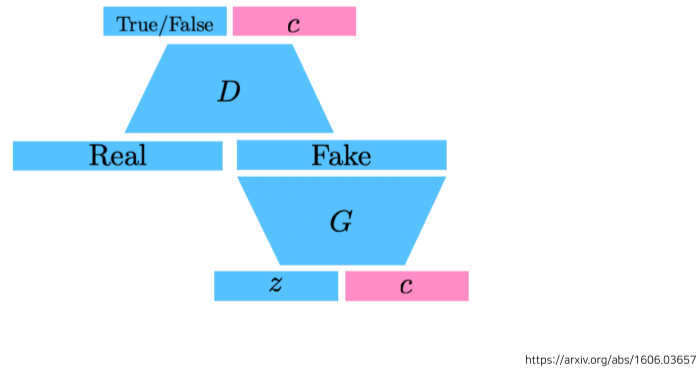
    [img. Info-GAN]

    • class를 추가로 인풋으로 넣어줌

    [img. 주어진 문장에 맞는 이미지를 만들어주는 Text2Image]

    • DALL-E와 비슷함

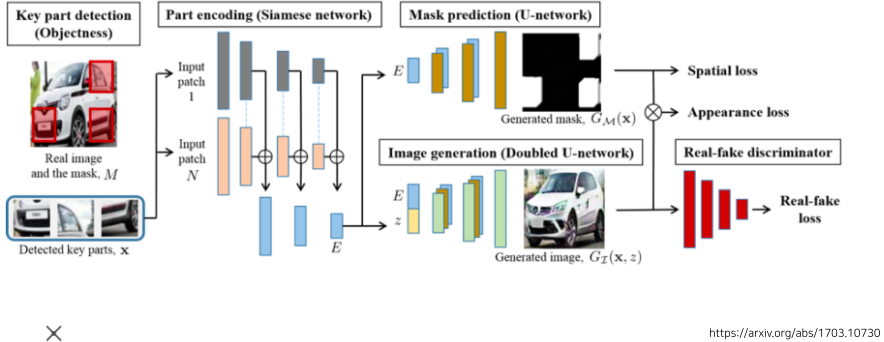
    [img. Puzzle-GAN]

    • 원래 이미지를 복원하는 모델

    [img. CycleGAN]

    • 이미지 내부의 도메인을 바꿔주는 모델

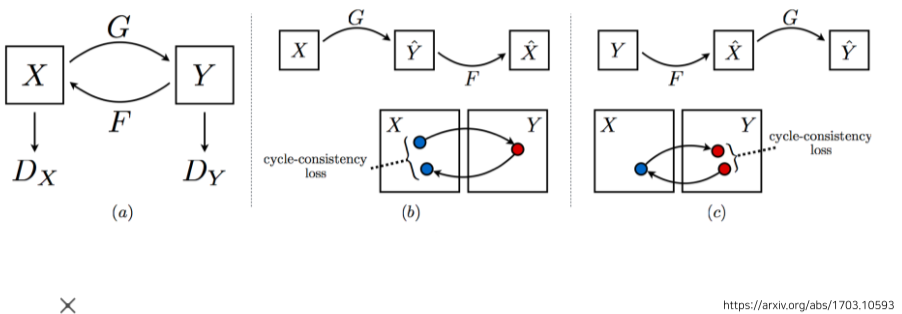
    [img. Cycle-consistency loss]

    • GAN 구조가 2개 들어있는 형식

    [img. Star-GAN]

    • 이미지를 컨트롤할 수 있게 해줌

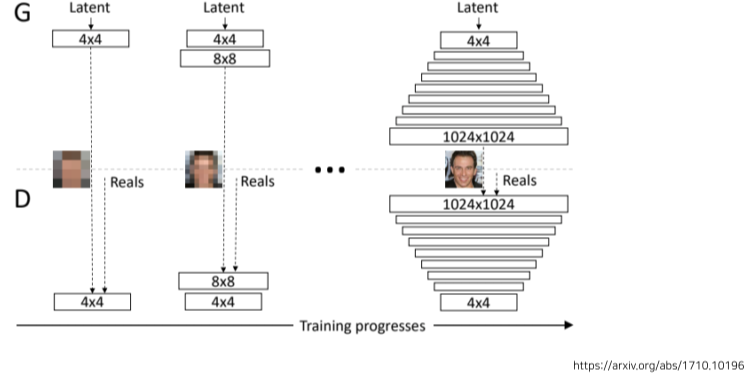
    [img. Progressive-GAN]

    • 고해상도의 이미지 생성하는 모델